
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центральная предельная теоремаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Данная теорема определяет условия, при которых возникает СВ с нормальным законом распределения – т.е. закон распределения суммы большого числа СВ Эта теорема впервые была сформулирована русским математиком Ляпуновым А.М. (1857-1918). Одна из простейших форм – относится к случаю одинаково распределенных слагаемых. Теорема. Если X1…Xn-случайные независимые величины имеющие одно т тоже распределение с математическим ожиданием m и дисперсией σ2, то при увеличении n закон распределения суммы
неограниченно приближается к нормальному. Теорема Ляпунова. Пусть X1, …,Xn – независимые случайные величины с математическими ожиданиями m1, …, mn и дисперсиями D1, …, Dn, причем при n→∞
При наличии данных условий закон распределения
неограниченно стремится к нормальному при n ®¥ Например, теоремы Муавра–Лапласа – частный случай ЦПТ. Если производится m независимых опытов, в каждом из которых событие А появляется с вероятностью р, то справедливо соотношение:
Упрощенный вариант – Если СВ есть сумма большого числа независимых СВ, влияние которых на всю сумму мало, то Х имеет закон распределения, близкий к нормальному.
Пример. Требуется произвести 60 выплат. Размер выплат случаен, но средняя выплата равна 50, а средне квадратичное отклонение равно 20. 1. Сколько должно быть денег в кассе, чтобы с вероятностью 0Б95 хватило всем? 2. Сколько денег с вероятностью 0,95 останется в кассе, если первоначально было 3500.
Решение. Суммарная выплата
Необходимый запас определяем с использованием функции Лапласа:
Остается 3500-3255,6=244.4.
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ Локальная теорема Муавра-Лапласа. Теорема Муавра-Лапласа устанавливает условия, при которых биномиальную случайную величину можно приближённо рассматривать как нормальную. Пусть X ~ B (n, p). При n ®¥ и любых фиксированных a и b, a £ b:
для любых m, удовлетворяющих неравенствам: a £ Ошибка приближения зависит от того, достаточно ли велико n, не слишком ли близко p к 0 или к 1 и каково интересующее нас значение m. Эта ошибка в настоящее время хорошо изучена и оценена; при необходимости всю нужную информацию можно найти в литературе.
Интегральная теорема Муавра-Лапласа. Пусть X ~ B (n, p). Тогда при n ®¥ и любых фиксированных a и b, a £ b:
Теорема Муавра-Лапласа позволяет уточнить связь относительной частоты и вероятности. По этой формуле можно приближённо находить вероятность a заданного отклонения относительной частоты от вероятности, вычислять необходимое число опытов n, при котором с данной вероятностью a указанное отклонение не превышает e. Исходное уравнение выглядит так: ВВЕДЕНИЕ Математической статистикой называется наука, занимающаяся методами обработки экспериментальных данных (ЭД), полученных в результате наблюдений над случайными явлениями. Перед любой наукой ставятся следующие задачи: Ø Описание явлений; Ø Анализ и прогноз; Ø Выборка оптимальных решений. Применительно к математической статистике пример задачи первого типа: пусть имеется статистический материал, представляющий собой случайные числа. Требуется его упростить, представить в виде таблиц и графиков, обеспечивающих наглядность и информативность представленного материала. Пример задачи второго типа: оценка (хотя бы приблизительная) характеристик случайных величин, например, математического ожидания, дисперсии и т.д. Какова точность полученных оценок. Одной из характерных задач третьего типа является задача проверки правдоподобия гипотез, которая формулируется следующим образом: можно ли предполагать, что имеющаяся совокупность случайных чисел не противоречит некоторой гипотезе (например о виде распределения, наличия корреляционной зависимости и т.д.). В курсе рассматриваются задачи всех трех типов: способы описания результатов опыта, способы обработки опытных данных и оценки по ним характеристик случайного явления, способы выбора разумных решений.
БАЗОВЫЕ ПОНЯТИЯ
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 780; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.255.58 (0.006 с.) |

 близок к нормальному.
близок к нормальному.

 .
.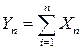

 . На основании центральной предельной теореме для одинаково распределенных слагаемых Y имеет приблизительно нормальное распределение с параметрами
. На основании центральной предельной теореме для одинаково распределенных слагаемых Y имеет приблизительно нормальное распределение с параметрами

 pmqn - m ~
pmqn - m ~ 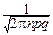 exp[-
exp[-  ] *)
] *) £ b.
£ b.
 .
.


