
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные величины. Закон распределения вероятностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Под с лучайной величиной понимается величина, которая в результате опыта со случайным исходом принимает то или иное значение. Возможные значения случайной величины образуют множество Ξ, которое называется множеством возможных значений случайной величины. Обозначения случайной величины: X, Y, Z; возможные значения случайной величины: x, y, z. Примеры случайных величин: 1. Опыт –бросание двух монет. Тогда Ξ ={(г,г), (г,ц), (ц,г), (ц,ц)}. Числовая функция Х (СВ Х)– число выпадений герба, определенная на множестве Ξ={0,1,2} – герб может выпасть 0,1,2 раза. 2. Опыт - работа ЭВМ после ремонта, случайная величина T – время наработки на отказ. Множество возможных значений Ξ – теоретически вся правая половина оси абсцисс. Множество возможных значений для этого опыта несчетно. В зависимости от вида множества Ξ случайные величины могут быть дискретными и недискретными. СВ Х называется дискретной, если множество ее возможных значений Ξ – счетное или конечное. Если множество возможных значений СВ несчетно, то такая СВ является недискретной. В теоретико-множественной трактовке основных понятий теории вероятностей случайная величина Х есть функция элементарного события: X =φ(ω), где ω – элементарное событие, принадлежащее пространству Ω. При этом множество Ξ возможных значений СВ Х состоит из всех значений, которые принимает функция φ(ω). Законом распределения СВ называется любое правило (таблица, функция), позволяющее находить вероятности всевозможных событий, связанных со случайной величиной. (То есть, всякое соотношение, устанавливающее связь между возможными значениями СВ и их вероятностями.) СВ будет полностью описана с вероятностной точки зрения, если мы зададим это распределение, т.е. в точности укажем, какой вероятностью обладает каждое событие. Про случайную величину мы будем говорить, что она подчинена данному закону распределения. 5.2. Ряд распределения дискретной случайной величины. Наиболее простую форму можно придать закону распределения дискретной случайной величины. Рядом распределения дискретной случайной величины называется таблица, в которой перечислены в порядке возрастания все возможные значения случайной величины X: x1, x2, …, xn, … и вероятности этих значений p1, p2, …, pn, …, где pi=P{X=xi} – вероятность того, что в результате опыта СВ Х примет значение xi (i =1,2,…, n, …).
Ряд распределения записывается в виде таблицы:
Так как события {X=x1}, {X=x2}, … несовместны и образуют полную группу, то сумма всех вероятностей, стоящих в нижней строке равна единице:
Многоугольник вероятностей – есть графическое изображение ряда вероятностей – по оси абсцисс откладываются возможные значения случайной величины, а по оси ординат – вероятности этих значений. Для наглядности полученные точки соединяются отрезками прямых. Многоугольник распределения, так же как и ряд распределения полностью характеризует случайную величину – и является одной из форм закона распределения. Функция распределения Наиболее общей формой закона распределения, пригодной для всех случайных величин (как дискретных, так и недискретных) является функция распределения. Функцией распределения случайной величины X называется вероятность того, что она примет значение меньшее, чем аргумент функции x: F (x)=P{ X < x }.
1. 2. 3. F (x) – неубывающая функция своего аргумента, т.е. при x 1< x 2 F (x 1) £ F (x 2). Доказательство этого свойства иллюстрируется рис. 5.2. Представим событие C ={ X < x2 } как сумму двух несовместных событий С=A+B, где A ={ X < x1 } и B ={ x1£X<x2 }. По правилу сложения вероятностей P (C)= P (A)+ P (B), т.е. P { X < x2 }= P { X < x1 }+ P{ x1£X<x2 }, или F(x2)=F(x1)+P{ x1£X<x2 }. Но P{ x1£X<x2 }£0, следовательно, F (x 1) £ F (x 2) 4. P(α£ X < β) = F (β) - F (α), для "[α,β[ÎR. (5.4) Доказательство этого свойства вытекает из предыдущего доказательства. Вероятность того, что случайная величина Х в результате опыта попадет на участок от α до β (включая α) равна приращению функции распределени я на этом участке. Таким образом, функция распределения F(x)любой случайной величины есть неубывающая функция своего аргумента, значения которой заключены между 0 и 1: 0≤F(x)≤1, причем F(-∞)=0, F(+∞)=1.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 506; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.83.45 (0.009 с.) |

 (5.1)
(5.1) Геометрически функция распределения интерпретируется как вероятность того, что случайная точка X попадет левее заданной точки X (рис. 5.1). Из геометрической интерпретации наглядно можно вывести основные свойства функции распределения.
Геометрически функция распределения интерпретируется как вероятность того, что случайная точка X попадет левее заданной точки X (рис. 5.1). Из геометрической интерпретации наглядно можно вывести основные свойства функции распределения.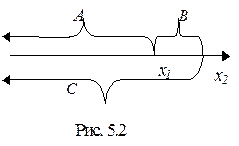
 F (-¥) = 0. (5.2)
F (-¥) = 0. (5.2) F (+¥) = 1. (5.3)
F (+¥) = 1. (5.3)


