
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типовые законы распределения нсвСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
8.1. Равномерное распределение. Непрерывная случайная величина Х равномерно распределена в интервале [ а; в ], если ее плотность вероятности в этом интервале постоянна, т.е. если все значения в этом интервале равновероятны:
Значение постоянной с определяется из условия нормировки:
Функция распределения:
Числовые характеристики равномерно распределенной случайной величины определяются так:
Среднее квадратичное отклонение равномерного распределения равно
Равномерное распределение случайной величины полностью определяется двумя параметрами: a и b – интервалом, на котором определена случайная величина. При необходимости можно определить параметры a и b равномерного распределения по известным значениям математического ожидания mX и дисперсии DX случайной величины. Для этого составляется система уравнений следующего вида:
из которой определяются искомые параметры. Вероятность попадания равномерно распределенной случайной величины в интервал [α,β) определяется так:
Например, шкала измерительного прибора проградуирована в некоторых единицах. СВ. Х – ошибка при округлении до ближайшего целого деления, которая с постоянной плотностью вероятности принимает любое значение между двумя соседними делениями. ХÎ(к, к+1). Ошибка измерения имеет равномерное распределение на интервале (-1/2,1/2). 8.2. Показательное (экспоненциальное) распределение. Непрерывная случайная величина Х, принимающая только положительные значения имеет показательное (или экспоненциальное) распределение, если
Положительная величина l называется параметром показательного распределения и полностью определяет его. Определим функцию распределения случайной величины. 1. при t <0
2. при t≥0
Таким образом, функция распределения имеет вид:
Графики плотности и функции распределения вероятностей экспоненциального распределения приведены на рис. 8.1.
Числовые характеристики случайной величины.
Проводя интегрирование по частям и учитывая, что при x→∞ e- x стремиться к нулю быстрее, чем возрастает любая степень x, находим:
Дисперсия случайной величины определяем по формуле:
Показательное распределение тесно связано с простейшим (стационарным пуассоновским) потоком событий. Интервал времени T между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром, равным интенсивности потока. Функция распределения СВ Т интервала времени между двумя соседними событиями в потоке:
Таким образом:
а плотность распределения равна
т.е. случайная величина имеет показательное распределение. 8.3. Нормальное распределение (закон Гаусса) Непрерывная случайная величина Х имеет нормальное распределение, если ее плотность вероятности имеет вид:
Определим числовые характеристики нормально распределенной случайной величины Х. Математическое ожидание:
Применяя замену переменной
получим
В полученном выражении первый интеграл равен нулю (интеграл в симметричных пределах от нечетной функции), а второй интеграл есть интеграл Эйлера-Пуассона:
Таким образом, математическое ожидание величины Х равно m: M[ X ]= m. Вычислим дисперсию СВ Х:
Применяя замену переменной (8.13) получим:
Интегрируя по частям, получим:
Первое слагаемое в фигурных скобках равно нулю (т.к.
Таким образом, нормальное распределение случайной величины полностью описывается двумя числовыми характеристиками: математическим ожиданием M [ X ] и средним квадратичным отклонением σ. Рассмотрим влияние параметров m и σ на кривую распределения. При изменении параметра m кривая f(x), не изменяя формы, будет смещаться вдоль оси абсцисс. Изменение σ равносильно изменению масштаба кривой по обеим осям; например, при удвоении σ масштаб по оси абсцисс удвоится, а по оси ординат уменьшится в два раза (рис. 8.3). Центральные моменты нечетной степени для нормально распределенной случайной величины определяются равны нуню; для вычисления центральных моментов четной степени используется рекуррентное соотношение следующего вида:
Определим вероятность попадания нормально распределенной случайной величины в интервал от α до β:
Сделав замену переменной t =(x - m)/ σ, получим:
Так как первообразная для e - x не выражается через элементарные функции, то для вычисления вероятностей событий, связанных с нормальными случайными величинами используют табулированную функцию Лапласа:
С помощью этой функции вероятность попадания нормально распределенной случайной величины на интервал от α до β определится так:
Функция Лапласа обладает следующими свойствами: 1. Φ(0)=0; 2. Φ(- х)=-Φ(х); 3. Φ(-∞)=0,5. Функция распределения нормально распределенной случайной величины через функцию Лапласа выражается так:
Значения функции Лапласа приведены в Приложении. Нормально распределенная случайная величина возникает в тех случаях, когда складывается много независимых (или слабо зависимых) случайных величин Х1, Х2, …, Xn. Тогда, каковы бы не были законы распределения отдельных случайных величин Xi, закон распределения их суммы будет близок к нормальному распределению. В частности, ошибки измерений распределяются по закону, близкому к нормальному.
Пример 8.1. Время безотказной работы аппаратуры является случайной величиной X, распределенной по показательному закону. Среднее время безотказной работы 100 ч. Найти вероятность того, что аппаратура проработает больше среднего времени. Решение. Плотность распределения
Пример 8.2. Имеется СВ, распределенная нормально с параметрами т, Решение.
По таблицам функции Лапласа (Приложение 2) находим Ф(3) = 0,49865. Тогда Пример 8.3. Для замера напряжения используются специальные датчики. Определить среднюю квадратичную ошибку датчика, если он не имеет математических ошибок, а случайные распределены по нормальному закону и с вероятностью 0,8 не выходят за пределы ±0,2. Решение. Из условия задачи следует, что
По таблице Лапласа находим аргумент
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 652; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.89.130 (0.008 с.) |

 (8.1)
(8.1) . (8.2)
. (8.2)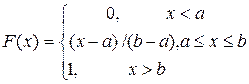 , (8.3)
, (8.3) (8.4)
(8.4) (8.5)
(8.5) (8.6)
(8.6) , (8.7)
, (8.7) , где
, где 
 , (8.8)
, (8.8) ,
, .
. (8.9)
(8.9)
 .
. (8.10)
(8.10) (8.11)
(8.11) .
. Рассмотрим на оси 0 t интервал времени T между двумя соседними событиями (рис. 8.2). Для того, чтобы выполнилось неравенство T < t, необходимо, чтобы на хотя бы одно событие потока попало на участок длины t; вероятность этого
Рассмотрим на оси 0 t интервал времени T между двумя соседними событиями (рис. 8.2). Для того, чтобы выполнилось неравенство T < t, необходимо, чтобы на хотя бы одно событие потока попало на участок длины t; вероятность этого
 ,
, ,
, (8.12)
(8.12)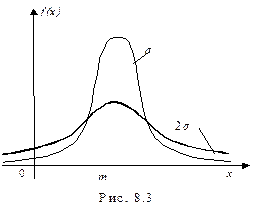 Кривая нормального распределения приведена на рис. 8.3.
Кривая нормального распределения приведена на рис. 8.3.
 (8.13)
(8.13)
 (8.14)
(8.14)


 при t→∞ убывает быстрее, чем возрастает любая степень t), второе слагаемое, согласно (8.14), равно
при t→∞ убывает быстрее, чем возрастает любая степень t), второе слагаемое, согласно (8.14), равно  , откуда
, откуда .
. (8.15)
(8.15)

 .
. (8.16)
(8.16) (8.16)
(8.16) Параметр
Параметр  . где тх = 100 — среднее время безотказной работы. Искомая вероятность f{X>mx} = P(X>100):
. где тх = 100 — среднее время безотказной работы. Искомая вероятность f{X>mx} = P(X>100):
 . Найти вероятность того, что СВ отклоняется от своего математического ожидания т на величину, большую чем
. Найти вероятность того, что СВ отклоняется от своего математического ожидания т на величину, большую чем  .
.
 = 1 - 2-0,49865 = 0,0027.
= 1 - 2-0,49865 = 0,0027. . Так как распределение ошибок нормальное, а математическое ожидание равно 0 (систематические ошибки отсутствуют), то
. Так как распределение ошибок нормальное, а математическое ожидание равно 0 (систематические ошибки отсутствуют), то
 , откуда
, откуда 


