
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Функції випадкових величин.Содержание книги
Поиск на нашем сайте
Приклад 1. Студент шукає необхідну інформацію в мережі Internet. Ймовірність знайти протягом півгодини відповідь на питання, використовуючи Google, Yandex, Rambler дорівнює відповідно 0,8; 0,6 та 0,5. Студент робить 1 запит у Google; 2 запита у Yandex та 3 у Rambler. Знайти закон розподілу Розв’язання.
Закон розподілу
Закон розподілу
Знайдемо закон розподілу
Закон розподілу випадкової величини
Закон розподілу
Остаточно закон розподілу
Обчислимо Маємо
Відповідь. Приклад 2. Випадкова величина Розв’язання. При Використовуючи формулу: Використовуючи останню формулу, маємо При Індивідуальні завдання 7 1. Випадкова величина 2. Два мисливці роблять по три постріли. Ймовірність влучення для кожного з них Зауваження. Ввести дві дискретні випадкові величини 3. Випадкова величина Тут Практичне заняття № 8 Тема: Розв’язання задач на основні закони розподілу дискретних випадкових величин. Приклад 1. У кожному із 100 контейнерів міститься по 8 виробів першого сорту, а решта 2 – браковані. Із кожного контейнера навмання беруть по одному виробу. Визначити Розв’язання. Цілочислова випадкова величина Х має біноміальний закон розподілу. Із умови задачі маємо:
За формулами:
Приклад 2. У деякому населеному пункті маємо 0,01% дальтоніків. Навмання вибирають 5000 мешканців цього населеного пункту. Визначити Розв’язання. Цілочислова випадкова величина Х розподілена за законом Пуассона. Із умови задачі:
Приклад 3. Гральний кубик підкидається до першої появи цифри 6. Визначити Розв’язання. Випадкова величина Х є цілочисловою, що має геометричний закон розподілу ймовірностей. За умовою задачі:
Індивідуальні завдання 8 Варіант 1. Серед дев’яти однотипних виробів п’ять відповідають вимогам стандарту, а решта – ні. Навмання береться шість виробів. Визначити закон розподілу цілочислової випадкової величини Х – появу числа виробів, що відповідають стандарту і обчислити для цієї величини Варіант 2. Під час штампування валиків імовірність відхилення кожного валика від стандартного розміру дорівнює 0,15. За робочу зміну робітником було проштамповано 800 валиків. Знайти закон Х – числа валиків, що не відповідають стандартному розміру, та її основні числові характеристики Варіант 3. У лабораторних умовах було висіяно 10000 насінин нового сорту ячменю. Імовірність того, що насінина ячменю не проросте в середньому становить 0,2. Визначити закон розподілу цілочислової випадкової величини Х – числа зернин ячменю, що проростуть, і обчислити Варіант 4. Радіотелефонна станція отримує цифровий текст. Унаслідок атмосферних завад імовірність спотворення цифри в середньому дорівнює 0,001. Було отримано текст, що налічує 2000 цифр. Знайти закон розподілу Х – числа спотворених цифр в отриманому тексті. Варіант 5. В урні міститься 100 кульок, із них 80 білі, а решта чорні. Кульки із урни виймають навздогад по одній із поверненням. Знайти закон розподілу Х – числа проведених експериментів, якщо вони здійснюються до першої появи чорної кульки. Чому дорівнюють Варіант 6. В електромережу містечка увімкнуто для освітлення вулиць у вечірню пору 20000 електролампочок. Імовірність того, що лампочка не перегорить протягом вечірнього часу дорівнює в середньому 0,95. Знайти закон розподілу Х – числа електролампочок, що не перегорять протягом вечірнього часу. Варіант 7. Для космічного корабля ймовірність зіткнення його з метеоритом малої маси дорівнює 0,001 протягом одного оберту навкіл Землі. Космічний корабель здійснив 900 обертів. Знайти закон розподілу Х – числа зіткнень космічного корабля із метеоритами малої маси. Варіант 8. Монета підкидається доти, доки вона випаде гербом. Знайти закон розподілу Х – числа здійснених підкидань. Варіант 9. Робітник за зміну обслуговує 14 однотипних верстатів-автоматів. Імовірність того, що верстат за зміну потребує уваги робітника становить 1/7. Знайти закон розподілу Х – числа верстатів-автоматів, що потребують уваги робітника за зміну. Варіант 10. За одну робочу зміну верстат-автомат виготовляє 400 однотипних деталей. Імовірність, що виготовлена верстатом деталь стандартна дорівнює 0,98. Знайти закон розподілу Х – числа стандартних деталей, виготовлених верстатом-автоматом за робочу зміну. Варіант 11. Серед 12 однотипних телевізорів 8 відповідають вимогам стандарту, а решта – ні. Навмання вибирають 5 телевізорів. Знайти закон розподілу Х – числа телевізорів, що відповідають вимогам стандарту серед 5 навмання вибраних. Варіант 12. Десять студентів складають залік з курсу „Вища математика”. Імовірність того, що студент складе залік, у середньому становить 0,91. Знайти закон розподілу Х – числа студентів, що складуть залік. Варіант 13. Серед одинадцяти однотипних виробів сім відповідають вимогам стандарту, а решта – ні. Навмання береться вісім виробів. Знайти закон розподілу Х – появу числа виробів, що відповідають стандарту і обчислити для цієї величини Варіант 14. Під час штампування валиків імовірність відхилення кожного валика від стандартного розміру дорівнює 0,13. За робочу зміну робітником було проштамповано 700 валиків. Знайти закон розподілу Х – числа валиків, що не відповідають стандартному розміру. Варіант 15. У лабораторних умовах було висіяно 12000 насінин нового сорту ячменю. Імовірність того, що насінина ячменю не проросте в середньому становить 0,3. Визначити закон розподілу цілочислової випадкової величини Х – числа зернин ячменю, що проростуть, і обчислити Варіант 16. Радіотелефонна станція отримує цифровий текст. Унаслідок атмосферних завад імовірність спотворення цифри в середньому дорівнює 0,002. Було отримано текст, що налічує 2200 цифр. Знайти закон розподілу дискретної випадкової величини Х – числа спотворених цифр в отриманому тексті. Варіант 17. В урні міститься 110 кульок, із них 90 білі, а решта чорні. Кульки із урни виймають навздогад по одній із поверненням. Визначити закон розподілу дискретної випадкової величини Х – числа проведених експериментів, якщо вони здійснюються до першої появи чорної кульки. Чому дорівнюють Варіант 18. В електромережу містечка увімкнуто для освітлення вулиць у вечірню пору 24000 електролампочок. Імовірність того, що лампочка не перегорить протягом вечірнього часу дорівнює в середньому 0,94. Знайти закон розподілу Х – числа електролампочок, що не перегорять протягом вечірнього часу. Варіант 19. Для космічного корабля ймовірність зіткнення його з метеоритом малої маси дорівнює 0,0015 протягом одного оберту навкіл землі. Космічний корабель здійснив 1000 обертів. Знайти закон розподілу дискретної випадкової величини Х – числа зіткнень космічного корабля із метеоритами малої маси. Варіант 20. Робітник за зміну обслуговує 16 однотипних верстатів-автоматів. Імовірність того, що верстат за зміну потребує уваги робітника становить 1/6. Знайти закон розподілу дискретної випадкової величини Х – числа верстатів-автоматів, що потребують уваги робітника за зміну. Варіант 21. За одну робочу зміну верстат-автомат виготовляє 420 однотипних деталей. Імовірність, що виготовлена верстатом деталь стандартна дорівнює 0,7. Знайти закон розподілу дискретної випадкової величини Х – числа стандартних деталей, виготовлених верстатом-автоматом за робочу зміну. Варіант 22. Серед 16 однотипних телевізорів 12 відповідають вимогам стандарту, а решта – ні. Навмання вибирають 6 телевізорів. Знайти закон розподілу дискретної випадкової величини Х – числа телевізорів, що відповідають вимогам стандарту серед 14 навмання вибраних. Варіант 23. Десять студентів складають залік з курсу „Вища математика”. Імовірність того, що студент складе залік, у середньому становить 0,92. Знайти закон розподілу дискретної випадкової величини Х – числа студентів, що складуть залік. Варіант 24. За одну робочу зміну верстат-автомат виготовляє 500 однотипних деталей. Імовірність, що виготовлена верстатом деталь стандартна дорівнює 0,75. Знайти закон розподілу дискретної випадкової величини Х – числа стандартних деталей, виготовлених верстатом-автоматом за робочу зміну. Варіант 25. Десять студентів складають залік з курсу „Вища математика”. Імовірність того, що студент складе залік, у середньому становить 0,94. Знайти закон розподілу дискретної випадкової величини Х – числа студентів, що складуть залік. Варіант 26. Серед десяти однотипних виробів шість відповідають вимогам стандарту, а решта – ні. Навмання береться сім виробів. Знайти закон розподілу Х – появу числа виробів, що відповідають стандарту і обчислити для цієї величини Варіант 27. Під час штампування валиків імовірність відхилення кожного валика від стандартного розміру дорівнює 0,15. За робочу зміну робітником було проштамповано 750 валиків. Знайти закон розподілу дискретної випадкової величини Х – числа валиків, що не відповідають стандартному розміру. Варіант 28. У лабораторних умовах було висіяно 9000 насінин нового сорту ячменю. Імовірність того, що насінина ячменю не проросте в середньому становить 0,2. Знайти закон розподілу величини Х – числа зернин ячменю, що проростуть, і обчислити Варіант 29. Радіотелефонна станція отримує цифровий текст. Унаслідок атмосферних завад імовірність спотворення цифри в середньому дорівнює 0,001. Було отримано текст, що налічує 2400 цифр. Знайти закон розподілу дискретної випадкової величини Х – числа спотворених цифр в отриманому тексті. Варіант 30. В урні міститься 120 кульок, із них 100 білі, а решта чорні. Кульки із урни виймають навздогад по одній із поверненням. Знайти закон розподілу дискретної випадкової величини Х – числа проведених експериментів, якщо вони здійснюються до першої появи чорної кульки. Чому дорівнюють Варіант 31. В електромережу містечка увімкнуто для освітлення вулиць у вечірню пору 22000 електролампочок. Імовірність того, що лампочка не перегорить протягом вечірнього часу дорівнює в середньому 0,96. Знайти закон розподілу дискретної випадкової величини Х – числа електролампочок, що не перегорять протягом вечірнього часу. Варіант 32. Для космічного корабля ймовірність зіткнення його з метеоритом малої маси дорівнює 0,0012 протягом одного оберту навкіл землі. Космічний корабель здійснив 960 обертів. Знайти закон розподілу дискретної випадкової величини Х – числа зіткнень космічного корабля із метеоритами малої маси. Варіант 33. Робітник за зміну обслуговує 15 однотипних верстатів-автоматів. Імовірність того, що верстат за зміну потребує уваги робітника становить 1/5. Знайти закон розподілу дискретної випадкової величини Х – числа верстатів-автоматів, що потребують уваги робітника за зміну. Варіант 34. За одну робочу зміну верстат-автомат виготовляє 360 однотипних деталей. Імовірність, що виготовлена верстатом деталь стандартна дорівнює 0,9. Знайти закон розподілу дискретної випадкової величини Х – числа стандартних деталей, виготовлених верстатом-автоматом за робочу зміну. Варіант 35. Серед 10 однотипних телевізорів 8 відповідають вимогам стандарту, а решта – ні. Навмання вибирають 6 телевізорів. Знайти закон розподілу дискретної випадкової величини Х – числа телевізорів, що відповідають вимогам стандарту серед 9 навмання вибраних. Практичне заняття № 9
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 785; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.209.101 (0.007 с.) |

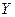 - кількість вдалих запитів серед 6 зроблених.
- кількість вдалих запитів серед 6 зроблених. - кількість вдалих запитів в Google;
- кількість вдалих запитів в Google;  - кількість вдалих запитів в Yandex;
- кількість вдалих запитів в Yandex;  - кількість вдалих запитів в Rambler. Знайдемо закон розподілу кожної з величин
- кількість вдалих запитів в Rambler. Знайдемо закон розподілу кожної з величин  ;
; 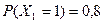

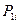



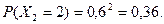

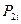







 , у допоміжній таблиці проведемо розрахунки
, у допоміжній таблиці проведемо розрахунки




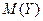 , використовуючи властивості математичного сподівання
, використовуючи властивості математичного сподівання  .
.


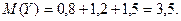

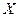 розподілена за нормальним законом з математичним сподіванням
розподілена за нормальним законом з математичним сподіванням  та дисперсією
та дисперсією  Знайти диференціальну функцію розподілу випадкової величини
Знайти диференціальну функцію розподілу випадкової величини 
 для
для 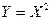 оберненою функцією є
оберненою функцією є  при
при 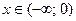 обернена функція
обернена функція 
 отримуємо
отримуємо  Тобто щільність розподілу
Тобто щільність розподілу 

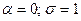 маємо
маємо 
 Знайти щільність розподілу випадкової величини
Знайти щільність розподілу випадкової величини 
 Знайти закон розподілу випадкової величини
Знайти закон розподілу випадкової величини 
 - кількість влучень для першого та другого мисливців та розглянути
- кількість влучень для першого та другого мисливців та розглянути 
 Знайти закон розподілу випадкової величини
Знайти закон розподілу випадкової величини  обчислити
обчислити 
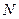 - номер варіанту;
- номер варіанту;  - кількість літер у прізвищі;
- кількість літер у прізвищі; 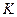 - кількість літер у повному імені.
- кількість літер у повному імені. , для дискретної випадкової величини Х – поява числа виробів першого сорту серед 100 навмання взятих.
, для дискретної випадкової величини Х – поява числа виробів першого сорту серед 100 навмання взятих. .
. дістанемо:
дістанемо: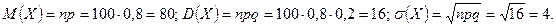
 . Згідно з формулами
. Згідно з формулами  ;
;  дістанемо:
дістанемо: ;
; 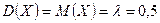 ;
;  .
. . Скориставшись формулами:
. Скориставшись формулами:  ;
;  , дістанемо:
, дістанемо: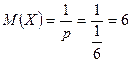 ;
;  ;
;  .
. .
.



