
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Визначення закону розподілу одновимірних випадкових величин. Обчислення числових характеристик.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Приклад 1. Студент складає іспити з трьох предметів. Імовірність здати перший, другий і третій іспити відповідно дорівнюють 1) Скласти закон розподілу випадкової величини Х – числа іспитів, які складе студент. 2) Побудувати многокутник розподілу ймовірностей. 3) Знайти функцію розподілу Розв’язання. 1. Можливі значення випадкової величини Х – це 0, 1, 2, 3. Позначимо події: А – студент здасть 1-й іспит; B – студент здасть 2-й іспит; С – студент здасть 3-й іспит. Тоді значенню
Значенню Х=1 відповідає складна подія
Значенню Х=2 відповідає складна подія
Значенню Х=3 відповідає найкраща ситуація, коли студент здасть всі три іспити, тоді Складемо закон розподілу
Перевіримо умову нормування
 - ламану лінію у точках з вершинами - ламану лінію у точках з вершинами    
імовірностей
1 2 3 х
3. Знайдемо функцію розподілу
Маємо:
Приклад 2. Проводяться чотири незалежних постріли по мішені. Імовірність влучення при одному пострілі постійна і дорівнює 1. Знайти закон розподілу 2. Обчислити Розв’язання. За умовою задачі випадкова величина Випадкова величина Значення Аналогічно обчислимо за формулою Бернуллі
Складемо закон розподілу
Перевірка:
Перевіримо обчислені числові характеристики для біноміального закону розподілу за короткими формулами:
Приклад 3. Студент підготував до заліку 1. Скласти закон розподілу 2. Побудувати многокутник розподілу ймовірностей. 3. Обчислити числові характеристики розподілу: Розв’язання.
1) За умовою задачі Маємо: Маємо закон розподілу
2) Побудуємо многокутник розподілу імовірностей ДВВ
0 1 2 3
3)
Початкові моменти:
Центральні моменти:
Обчислимо асиметрію Обчислимо ексцес Приклад 4. Випадкова величина
1. Знайти невідомий параметр 2. Знайти 3. Знайти диференціальну функцію розподілу і побудувати її графік. 4. Обчислити 5. Обчислити Розв’язання. 1. Для знаходження невідомого параметра Знайдемо диференціальну функцію розподілу
Маємо Розв’яжемо відносно 2. Знайдемо Графік
3. Знайдемо Графік
4.
Мода Медіану
Знайдемо початкові моменти:
Знайдемо центральні моменти
Обчислимо асиметрію: Обчислимо ексцес: 5. Знайдемо Індивідуальні завдання 5 Завдання 1. Розв’язати задачу, представлену в прикладі 1, покладаючи Завдання 2. Розв’язати задачу, представлену в прикладі 2, покладаючи Завдання 3. Розв’язати задачу, представлену в прикладі 3 при таких значеннях Варіанти 1-10: Варіанти 11-20: Варіанти 21-30: Варіанти 31-35: де К - номер Вашого варіанта.
Завдання 4. Випадкова величина Практичне завдання № 6 Тема:Обчислення числових характеристик системи двох дискретних випадкових величин. Приклад 1. Система двох дискретних випадкових величин
1. Знайти невідомий параметр системи 2. Знайти ряди розподілу кожної випадкової величини 3. Обчислити числові характеристики системи 4. Знайти умовний закон розподілу ДВВ 5. Знайти умовний закон розподілу ДВВ 6. Знайти закон розподілу ДВВ 7. Обчислити імовірність події Розв’язання. 1. Умова нормування ряду розподілу системи ДВВ Маємо:
Маємо остаточно закон розподілу
1. Знайдемо ряд розподілу одновимірної ДВВ
Отже, маємо ряд розподілу для ДВВ
Одновимірна функція цього розподілу Знайдемо ряд розподілу для ДВВ
Отже, маємо закон розподілу ДВВ
Одновимірна функція розподілу
2. Обчислимо числові характеристики для системи ДВВ
Обчислимо кореляційний момент
Отже, Оскільки Оскільки Коефіцієнт кореляції:
Оскільки 3. Знайдемо умовний закон розподілу ДВВ Користаючи формулою умовної імовірності
Отже, маємо умовний закон розподілу ДВВ
Зауваження.Імовірність події 5. Знайдемо умовний закон розподілу ДВВ X при умові
Отже, умовний закон розподілу ДВВ X при умові
Зауваження.Імовірність 6. Знайдемо закон розподілу ДВВ Розмістимо у правих верхніх кутах клітин закону розподілу системи ДВВ
Маємо:
звідки
Отже, закон розподілу ДВВ
7.Обчислимо
Подія Отже, Індивідуальні завдання 6 Виконати всі завдання 1-7, представлені в прикладі 1 для системи двох дискретних величин Практичне заняття № 7
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 655; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.36.89 (0.01 с.) |


 та побудувати її графік, якщо
та побудувати її графік, якщо 


 відповідає ситуація, коли студент не здасть жодного іспиту, тобто
відповідає ситуація, коли студент не здасть жодного іспиту, тобто 

 яка полягає у тому, що студент здасть лише один з трьох іспитів. Тоді
яка полягає у тому, що студент здасть лише один з трьох іспитів. Тоді 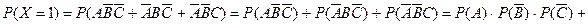

 яка полягає у тому, що студент здасть два іспити з трьох,
яка полягає у тому, що студент здасть два іспити з трьох, 








 – многокутник розподілу
– многокутник розподілу







 Побудуємо графік функції розподілу:
Побудуємо графік функції розподілу:

 – числа влучень у мішень.
– числа влучень у мішень.

 якщо
якщо 




 відповідає жодному влученню з чотирьох пострілів, тоді
відповідає жодному влученню з чотирьох пострілів, тоді 
 імовірності подій:
імовірності подій: ;
; ;
; ;
; .
.








 ;
;  ;
;  .
. питань з
питань з  питань програми. Білет містить
питань програми. Білет містить  питань.
питань.
 якщо
якщо 

 обчислюємо за формулою:
обчислюємо за формулою: 











 .
.
 многокутник розподілу імовірністей ДВВ
многокутник розподілу імовірністей ДВВ 

 .
. бо
бо  при
при  .
.
 - початковий момент першого порядку
- початковий момент першого порядку початковий момент 2-го порядку
початковий момент 2-го порядку початковий момент 3-го порядку
початковий момент 3-го порядку початковий момент 4-го порядку.
початковий момент 4-го порядку. - центральний момент 2-го порядку
- центральний момент 2-го порядку - центральний момент 3-го порядку.
- центральний момент 3-го порядку. - центральний момент 4-го порядку.
- центральний момент 4-го порядку.


 .
.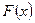 і побудувати її графік.
і побудувати її графік.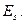




 звідки
звідки  ,
,  Оскільки при
Оскільки при  правий кінець проміжка
правий кінець проміжка  не узгоджується з лівим кінцем його
не узгоджується з лівим кінцем його  то це значення
то це значення  є стороннім. Отже,
є стороннім. Отже, 










 відсутня, маємо антимодальний закон розподілу.
відсутня, маємо антимодальний закон розподілу. знайдемо з умови
знайдемо з умови 
 звідки
звідки 

 початковий момент 1-го порядку.
початковий момент 1-го порядку. – початковий момент 2-го порядку.
– початковий момент 2-го порядку. – початковий момент 3-го порядку.
– початковий момент 3-го порядку. – початковий момент 4-го порядку.
– початковий момент 4-го порядку. , використовуючи значення початкових моментів
, використовуючи значення початкових моментів  :
: – центральний момент 2-го порядку.
– центральний момент 2-го порядку. – центральний момент 3-го порядку.
– центральний момент 3-го порядку. – центральний момент 4-го порядку.
– центральний момент 4-го порядку. .
. .
. .
.

 де
де  де
де 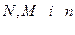 :
:











 Виконати завдання прикладу 4 (в п. 5 задачі обчислити ймовірність
Виконати завдання прикладу 4 (в п. 5 задачі обчислити ймовірність  ).
). задана таблицею розподілу.
задана таблицею розподілу. х y
х y








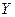 та знайти одновимірні функції їх розподілів.
та знайти одновимірні функції їх розподілів. . Обчислити математичне сподівання цього розподілу.
. Обчислити математичне сподівання цього розподілу. та обчислити
та обчислити  .
. .
. , де
, де 
 звідки
звідки 
 :
:


 ;
;  .
.
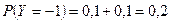 ;
;  ;
;  ;
;  .
.


 має вигляд:
має вигляд:







 де
де 

 то між ДВВ X та Y існує кореляційний зв'язок.
то між ДВВ X та Y існує кореляційний зв'язок. то цей кореляційний зв'язок має «відємний» характер: із зростанням однієї величини інша величина спадає.
то цей кореляційний зв'язок має «відємний» характер: із зростанням однієї величини інша величина спадає.
 то величина
то величина  свідчить про помірний зв'язок між X таY.
свідчить про помірний зв'язок між X таY. .
. , маємо
, маємо 


 .
.





 ми знайшли в пункті 2.
ми знайшли в пункті 2.





 ми знайшли в пункті 2.
ми знайшли в пункті 2. як добуток
як добуток  відповідних рядка і стовпця, перетин яких утворює ці клітини.
відповідних рядка і стовпця, перетин яких утворює ці клітини. y
x
y
x









 користуючись законом розподілу системи ДВВ
користуючись законом розподілу системи ДВВ 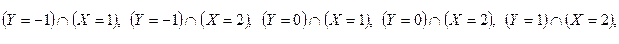 тоді
тоді 

 , заданої таблицею розподілу.
, заданої таблицею розподілу.


