
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Обчислення коефіцієнта кореляції, побудова прямих регресій.Содержание книги
Поиск на нашем сайте Приклад 1. Отримано вибіркові данні про ціни на квартири та загальну їх площу в місті N, січень 2009 р.
Необхідно: 1. Побудувати графік залежності між змінними, по якому необхідно підібрати модель рівняння регресії. 2. Розрахувати параметри рівняння регресії методом найменших квадратів. 3. Знайти коефіцієнт еластичності. 4. Оцінити тісноту зв’язку між змінними за допомогою показників кореляції та детермінації. Розв’язання. Графік залежності змінних Х та Y будується у прямокутній системі координат. На осі абсцис відкладаються значення факторної ознаки Х, а по вісі ординат – результативної ознаки Y. Враховуючи невелике число пар значень змінних, по кожній з них виділимо 5 інтервалів, використовуючи формулу:
де h – довжина інтервалу, хmin – найменше значення ознаки, хmax – найбільше значення ознаки, k – число інтервалів. Для змінної Х: В результаті отримаємо наступні границі інтервалів: 33+16=49; 49+16=65; 65+16=81; 81+16=97; 97+16=113. Аналогічно, для змінної Y: На графік наносяться точки, координати яких відповідають значенням Y та X. Характер розташування точок на графіку показує, що зв'язок між змінними може виражатися лінійним рівнянням регресії:
Рис.1. Залежність ціни на квартири від загальної їх площі 2. Параметри рівняння регресії знаходимо методом найменших квадратів, шляхом складання та розв’язання системи нормальних рівнянь. Для проведення усіх розрахунків будується допоміжна таблиця. В таблиці усі середні знаходяться за формулою середньої арифметичної простої: Підставимо отриманні суми в систему рівнянь, враховуючи, що n=15:
Розв’язавши систему, отримуємо b0=4,7743; b1=0,3018. Параметри рівняння регресії також можна знайти за формулами, які отримано шляхом використання правила Крамера розв’язання системи лінійних алгебраїчних рівнянь.
Допоміжна таблиця:
Невеликі розбіжностів результатах розрахунків пояснюються заокругленням середніх значень в другому випадку. Таким чином, рівняння регресії має вигляд Коефіцієнт регресії показує, що при збільшені загальної площі квартири на 1 м2 ціна квартири в середньому збільшиться на 0,3018 тис. У.є., або на 301,8 у.є. Якщо в рівнянні регресії підставити фактичні значення змінної Х, то визначаються можливі (теоретичні) значення змінної 3. При лінійній формі зв’язку середній коефіцієнт еластичності знаходиться за формулою Э Э= Коефіцієнт еластичності показує, що при збільшенні загальної площі квартири на 1% її ціна в середньому виросте на 0,806 %. 4. При лінійній залежності, ступінь тісноти зв’язку між змінними
Так як значення коефіцієнта кореляції близьке до одиниці, то між ознаками зв'язок дуже тісний, пряма, близька до лінійної функціональної. Коефіцієнт детермінації r2=0,9222=0,850 показує, що 85 % відмінностей в ціні квартир пояснюється варіацією їх загальної площі, а 15 % - іншими, неврахованими факторами (місцезнаходження квартир, благоустрійтериторії, розвинена інфраструктура т. і.). Індивідуальні завдання 15 1. Досліджується два типи цінних паперів, дохідність яких дорівнює відповідно X та Y. Мета дослідження виявити взаємозалежні коливання курсів цінних паперів. Необхідно: - побудувати графік залежності між змінними, по якому необхідно підібрати модель рівняння регресії; - розрахувати параметри рівняння регресії методом найменших квадратів; - знайти коефіцієнт еластичності; - оцінити тісноту зв’язку між змінними за допомогою показників кореляції та детермінації.
Числові значення параметрів: N – номер варіанту; K – кількість літер прізвищі. 2. Припускаючи, що
Числові значення параметрів: N – номер варіанту; K – кількість літер прізвищі. Зауваження до завдання 2. Система нормальних рівнянь для параметрів
Після обчислення необхідних сум, дана система може бути розв’язана Вами у будь-який з відомих Вам з курсу «Вища математика для економістів» способів: методом Гауса, Жордано-Гауса, оберненої матриці, Крамера. Практичне заняття № 16 Тема: Випадкові процеси Приклад 1. Випадковий процес визначається формулою Розв’язання. Щільність нормального розподілу при Для обчислення математичного сподівання використаємо формулу
Для обчислення дисперсії використовуємо властивості дисперсії
Середнє квадратичне відхилення Приклад 2. Задано матрицю перехідних ймовірностей ланцюга Маркова Розв’язання. Має місце формула для визначення матриці переходів за
Індивідуальна робота 16 1. Випадковий процес визначається формулою
2. Задано матрицю перехідних ймовірностей ланцюга Маркова
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 482; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |


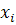
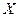 - загальна площа квартири, кв.м;
- загальна площа квартири, кв.м; 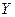 - ринкова ціна квартири, тис. у.е.
- ринкова ціна квартири, тис. у.е.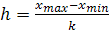 ,
,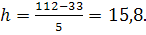 Для інтервалу округлюється в сторону збільшення для зручного значення,
Для інтервалу округлюється в сторону збільшення для зручного значення,  =16.
=16. Границі інтервалів складають: 13; 18; 23; 28; 33; 38.
Границі інтервалів складають: 13; 18; 23; 28; 33; 38. .
.
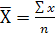 .
.
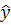
 2
2
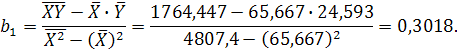
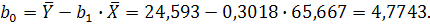
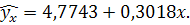
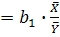 , де
, де 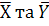 – середні значення ознак.
– середні значення ознак.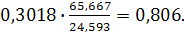
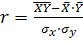 , де
, де 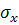 та
та 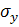 – середні квадратичні відхилення по X та Y.
– середні квадратичні відхилення по X та Y.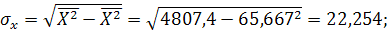
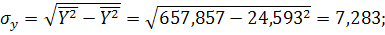
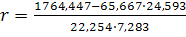 =0,922.
=0,922.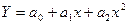 , за допомогою методу найменших квадратів оцінити параметри
, за допомогою методу найменших квадратів оцінити параметри  рівняння регресії
рівняння регресії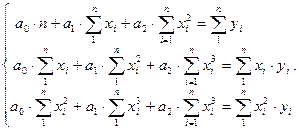
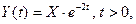 де
де 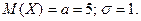 Знайти математичне сподівання та дисперсію випадкового процесу
Знайти математичне сподівання та дисперсію випадкового процесу 
 дорівнює
дорівнює  .
.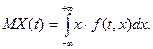
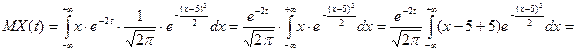
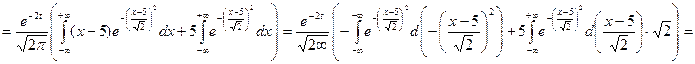
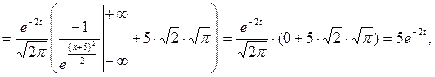 тобто
тобто 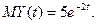
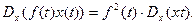
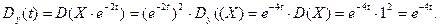
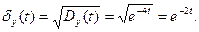
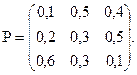 Знайти матрицю переходу за 2 кроки.
Знайти матрицю переходу за 2 кроки. кроків
кроків  За формулою
За формулою 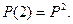
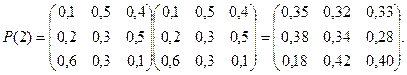
 Знайти математичне сподівання та дисперсію випадкового процесу
Знайти математичне сподівання та дисперсію випадкового процесу 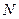 - номер варіанту;
- номер варіанту; 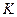 - кількість літер у прізвищі.
- кількість літер у прізвищі.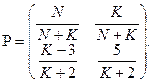 Знайти матрицю переходу за 3 кроки.
Знайти матрицю переходу за 3 кроки.


