Атрибутивні та варіаційні ряди розподілу

Урок 63

Ряд розподілу. Статистична залежність, коефіцієнт парної лінійної кореляції, кореляційна таблиця. Побудова інтервальних рядів розподілу. Побудова діаграм рядів розподілу. Побудова лінійної регресійної моделі. Обчислення коефіцієнтів парної лінійної регресії. Поняття кореляції статистичних показників. Розрахунок коефіцієнта кореляції за допомогою стандартної функції.

Мотивація.

У попередньому розділі ми досліджували вибірки, дані в яких були незгруповані, тобто являли собою просто послідовності чи­сел. За такою послідовністю можна обчислити певні статистичні показники, але неможливо визначити тенденцію зміни значень досліджуваної ознаки. Наприклад, якщо є відомості про доходи 1000 осіб, можна визначити середній дохід, стандартне відхилен­ня величини доходу, проте важко сказати, як змінюється кіль­кість осіб, що отримують той чи інший дохід, зі зростанням його величини.

Вивчення нового матеріалу.

Статистичні ряди розподілу

Щоб дати відповідь на це питання, потрібно згрупува­ти дані, наприклад визначити кількість людей, що отримують дохід до 1000 грн, від 1000 до 2000 грн, від 2000 до 3000 грн тощо. У результаті ми отримаємо таблицю на кшталт табл. 10.1.

Побудована таблиця називається статистичним рядом розподілу. Загалом ряд розподілу — це два набори значень однакової довжи­ни. В одному наборі представлені значення певноїознаки (у табл. 10.1 це величина доходу), а в іншому — частоти, тобто кількості разів, коли під час статистичного спостереження було отримано відповідне значення ознаки. Інакше кажучи, ідеться про розподіл певних об’єктів за певною ознакою. Наприклад, у табл. 10.1 на­ведено розподіл осіб за величиною доходу. Величина доходу — це ознака, а кількості осіб — частоти.

За рядом розподілу вже можна визначити тенденцію зміни зна­чень досліджуваної ознаки. Так, з табл. 10.1 видно, що з ростом доходу від 0 до 2000 грн кількість осіб, які отримують цей дохід, зростає, а коли дохід перевищує 2000 грн, тенденція зворотна: що вище дохід, то менша кількість людей його отримує.

Атрибутивні та варіаційні ряди розподілу

Розрізняють атрибутивні та варіаційні ряди розподілу. Якщо за основу групування узята якісна ознака, то це атрибутивний ряд розподілу (розподіл за видами продукції, професіями, статтю, на­ціональною або географічною приналежністю тощо). Якщо ряд розподілу побудований за кількісною ознакою, то такий ряд є варіаційним (за розміром доходу, стажем роботи, числом праців­ників на підприємстві тощо).

Наприклад, наведений у табл. 10.1 ряд розподілу осіб за доходом є варіаційним, а ряд розподілу осіб за професіями, який наведено у табл. 10.2, — атрибутивним.

Побудова рядів розподілу

Припустимо, що результати статистичних спостережень необхідно згрупувати, побудувавши ряд розподілу. Ця операція виконуєть­ся у кілька етапів. Насамперед необхідно визначити, який ряд розподілу будувати — інтервальний чи дискретний. Критерій та­кий: якщо ознака може набувати лише невелику кількість різних значень (у межах одного-двох десятків), будуйте дискретний ряд розподілу, інакше — інтервальний.

ПРИМІТКА. Не плутайте випадок, коли ознака представлено у вибірці не­великою кількістю значень, з випадком, коли вона може набувати невеликої кількості значень у генеральній сукупності. Наприклад, якщо є вибірка з відомостями про зріст семи людей, то це ще не означає, що величина «зріст» може мати лише сім значень. А якщо є вибірка днів тижня, то величина «день тижня» дійсно може набувати лише семи різних значень.

Для побудови дискретного ряду розподілу слід виписати всі мож­ливі значення ознаки, а потім підрахувати, скільки разів кожне з них трапляється у вибірці — це будуть частоти. У Microsoft Excel для підрахунку частот слід застосувати функцію СЧЕТЕСЛИ, про яку йшлося на уроці 44. Розглянемо детальніше принцип побудови інтервального ряду розподілу.

Отже, для побудови за вибіркою х1, …, хn ряду розподілу, що скла­дається з m рівних інтервалів, необхідно виконати такі кроки.

1. Визначити найбільшу та найменшу варіанти — x_min та х_max.

2. Визначити величину інтервалу h = .

3. Визначити межі інтервалів [у₀;у₁], [у₁;у₂], …, [у_m-1, y_m] за формулами:

y₀=x_max; y_i+1=y_i + h, i=0, …, m-1.

Тобто нижня межа першого інтервалу дорівнює найменшій варіанті, а кожна наступна межа більша за попередню на h.

4. Підрахувати, скільки варіант потрапляє у кожен інтервал — це і будуть частоти. В Excel це можна зробити за допомогою функції ЧАСТОТА, яка має два аргументи:

ЧАСТОТА(діапазон_ ви6ірки;діапазон_меж_ інтервалів)

Перший аргумент — це діапазон, що містить вибірку, а другий — діапазон усіх меж інтервалів, за винятком у₀ та у_m (тобто усіх меж між інтервалами). Результатом функції буде на­бір частот, що відповідають кожному інтервалу. Ви вперше стикаєтеся з функцією, результатом якої є діапазон значень, а не окреме значення. Її і вводити потрібно дещо інакше, ніж інші функції. А саме, слід виділити весь діапазон, де місти­тимуться результати, ввести формулу функції та натиснути клавіші Ctrl+Shift+Enter.

Приклад використання функції ЧАСТОТА наведено на рис. 10.1, а.

Тут вибірка міститься в діапазоні А2:А21, xmin = 0, хтах = 100 і нам потрібно побудувати ряд розподілу з п’яти інтервалів. Межами між інтервалами будуть числа 20, 40, 60, 80 — вони містяться в діапазоні D2:D5. Функцію ЧАСТОТА введено в діапазон G2:G6, де ми бачимо результати її обчислення, тобто частоти. Процес вве­дення функції ЧАСТОТА зображено на рис. 10.1, б.

Коефіцієнт кореляції

Міцність зв’язку між двома величинами можна виразити і за допо­могою коефіцієнта кореляції. Це число k з інтервалу [-1, 1]. Якщо k близьке до -1, то кореляційний зв’язок між величинами є обер­неним, а якщо k близьке до 1 — прямим. Чим ближче k до нуля, тим кореляційний зв’язок слабший. Якщо говорити більш доклад­но, то міцність лінійного кореляційного зв’язку оцінюється так:

· |k|> 0,8 — сильний кореляційний зв’язок;

· 0,4 |k| < 0,8 — кореляційний зв’язок наявний;

· |k| < 0,4 — кореляційний зв’язок відсутній,

У Microsoft Excel для обчислення коефіцієнта кореляції вико­ристовується функція КОРРЕЛ(діапазон_1;діапазон_2), де діапазони діапазонні та діапазон_2 містять набори значень, між якими шукається залежність. У разі визначення коефіцієнта ко­реляції двох вибірок, поданих на рис. 10.5, такими масивами бу­дуть дані у діапазонах В2:Н2 та ВЗ:НЗ. Результатом функції КОРРЕЛ у нашому випадку буде число 0,9862, що свідчить про наявність дуже сильного кореляційного зв’язку між концентрацією чадного газу в повітрі та кількістю хронічно хворих на астму.

Зазначимо, що функція КОРРЕЛ визначає коефіцієнт лінійної ко­реляції, яка свідчить про наявність саме лінійного зв’язку між ознаками. Цей зв’язок буде тим сильніший, чим ближче до певної прямої розташовані точки на діаграмі розсіювання. Насправді існують й інші типи зв’язків. Наприклад, той факт, що точки на діаграмі розсіювання розташовані близько до певної парабо­ли, свідчить про наявність між ознаками квадратичного зв’язку; щоправда, коефіцієнт лінійної кореляції при цьому може бути незначним.

Кореляційна матриця

Коли потрібно порівняти не два, а більше масивів експерименталь­них даних, будують кореляційну матрицю — таблицю, у якій коефіцієнти кореляції між ознаками розташовані на перетині від­повідних рядків і стовпців. Для побудови кореляційної матриці використовують інструмент Кореляція, який запускається за допо­могою команди Сервіс ► Аналіз даних ► Кореляція.

ПРИМІТКА. Якщо меню Сервіс не містить команди Аналіз даних, необхід­но виконати команду Сервіс ► Надбудови та встановити прапорець Пакет аналізу.

Регресійний аналіз

Як уже зазначалося, основне завдання регресійного аналізу — прогнозування. Щоб навести приклад задачі на прогнозування, повернімось до вибірок з табл. 10.8. Значення факторної ознаки (концентрації чадного газу), отримані в результаті статистичного спостереження, коливаються в межах від 1,2 до 4,8 мг/м3. Для цих значень рівень захворюваності на астму відомий. Але задамо­ся питанням: яким буде цей рівень, якщо концентрація чадного газу становитиме 10 мг/м3? Тобто спробуємо спрогнозувати зна­чення результативної ознаки у разі виходу значення факторної ознаки за межі інтервалу вибірки.

Основним методом, який використовується для прогнозування, є побудова на основі вибіркових даних рівняння регресії вигляду y=f(x), що зв’язує факторну ознаку х і результативну ознаку у, та визначення за цим рівнянням невідомих значень результатив­ної ознаки. Рівняння можна подати як аналітично (за допомогою формул), так і графічно. Згадана вище лінія тренду — це не що інше, як графік рівняння регресії.

У Microsoft Excel передбачена можливість автоматичної побудови лінії тренду. Для цього спочатку слід виділити діаграму розсіюван­ня та виконати команду Діаграма ► Додати лінію тренду.Далі у вікні Лінія тренду на вкладці Тип (рис. 10.7, а) потрібно вибрати тип за­лежності між факторною та результативною ознаками — лінійна, поліноміальна (квадратична, кубічна тощо), логарифмічна та ін. На вкладці Параметри цього вікна (рис. 10.7, б) можна задати, зокрема, величину прогнозу (на скільки прогнозоване значення буде більшим за найбільше вибіркове чи меншим за найменше вибіркове). Це роблять за допомогою лічильників вперед на та на­зад на в області Прогноз.

На рис. 10.8 показано графік лінії тренду, доданий до точкової діаграми, зображеної на рис. 10.5. Величина прогнозу вперед для цього графіка становить 5 одиниць. З графіка видно, що за кон­центрації чадного газу 10 мг/м3 рівень захворюваності на астму становитиме приблизно 120 людей на 1000 жителів міста.

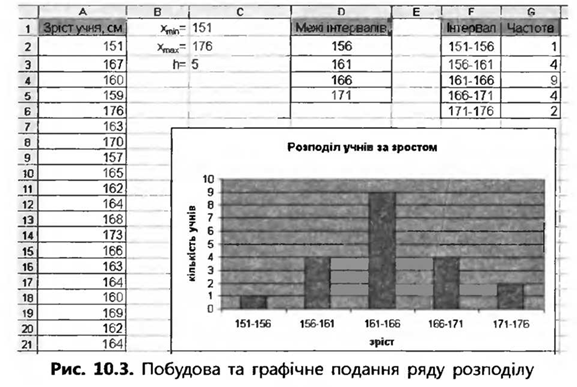
Коефіцієнт детермінації

Близькість рівняння регресії та лінії тренду до вибіркових да­них характеризується величиною коефіцієнта детермінації R² (0 < R² < 1). Рівняння регресії найбільше відповідає дійсності, коли R² наближається до свого максимального значення. Цей по­казник використовується в першу чергу для порівняння різних моделей прогнозу та вибору найкращої з них. На точковій діагра­мі як значення R², так і саме рівняння регресії можна відобразити біля лінії тренду (див. рис. 10.8). Для цього на вкладці Параметри вікна Лінія тренду слід встановити прапорці показувати величину віро­гідності апроксимації (R^2) на діаграмі та показувати рівняння на діаграмі (див. рис. 10.7, б). Для лінії тренду, яка наведена на рис. 10.8, R² = 0,9726. Це означає, що лінійне рівняння регресії добре узгод­жується з вибірковими даними.

Виконання вправи 3.

Практичне завдання.

Вправа 1. Побудова інтервального ряду розподілу

У файлі Bnpaвa_1.xIs наведено відомості про зріст учнів класу. По­трібно побудувати ряд розподілу учнів за зростом з п’ятьма рівни­ми інтервалами, зобразити його графічно та зробити висновок щодо характеру зв’язку між зростом та кількістю учнів цього зросту.

1. Відкрийте файл Bnpaвa_1.xls. У клітинки С1 та С2 уведіть формули для обчислення мінімального і максимального зросту учня: = MIN(A2:A21) та =МАХ(А2:А21). Ці значення мають бути такими: x_min = 151, x_max = 176.

2. У клітинці С3 обчисліть величину інтервалу групування h = . Вона повинна дорівнювати 5.

3. Обчисліть межі між інтервалами у клітинках D2:D5. У клітин­ці D2 обчисліть значення межі у1 = х_min + h. У клітинку D3 уведіть формулу =D2+C$3. Скопіюйте цю формулу у клітинки D4:D5, і ви отримаєте значення всіх інших меж. Фактично ми реалізували формулу yi+1=yi + h. Оскільки значення уі змінюється, посилання D2 є відносним. А оскільки величина h незмінна, номер рядка у посиланні С$3 зафіксовано.

4. Уведіть межі інтервалів у клітинки F2:F6 (рис. 10.3).

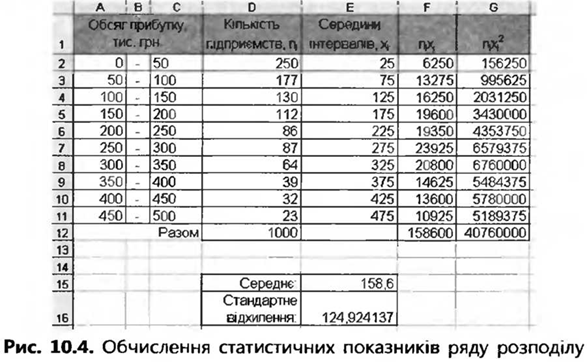
5. Виділіть діапазон G2:G6 та, скориставшись кнопкою fx (Встав­ка функції), уведіть функцію ЧАСТОТА. Її аргументи будуть та­кими: діапазон вибірки — А2:А21, діапазон меж інтервалів — D2:D5. Увівши аргументи функції, не клацайте кнопку ОК, а натисніть клавіші Ctrl+Shift+ Enter. Частоти буде обчислено.

6. Самостійно створіть гістограму частот (див. рис. 10.3). Як будувати та форматувати діаграми, ви знаєте з уроку 46-47.

7. Уведіть у клітинку F2 формулу, після копіювання якої в діа­пазон F3:F6 у ньому буде автоматично відображено інтервали, як на рис. 10.3.

Вправа 2. Обчислення статистичних показників

У файлі Bnpaвa_2.xls показано ряд розподілу підприємств міста N за прибутком. Обчисліть середній прибуток та стандартне відхи­лення прибутку цих підприємств. Зробіть висновки.

1. Відкрийте файл Bnpaвa_2.xls. У ньому на аркуші Аркуші на­ведено інтервальний ряд розподілу: у стовпці А вказано нижні межі інтервалів, у стовпці С — верхні, у стовпці D зазначено частоти.

2. Щоб обчислити статистичні показники, інтервальний ряд роз­поділу необхідно перетворити на дискретний. Для цього слід насамперед обчислити середини інтервалів. Уведіть у клітин­ку Е2 формулу =(А2+С2)/2, скопіюйте її в діапазон ЕЗ:Е11, і се­редини інтервалів буде відображено у стовпці Е.

3. Обчисліть величини nіxі та nixi², де ni — частоти, a xi — се­редини інтервалів. Для цього введіть у клітинки F2 та G2 формули =D2*E2 та =D2*E2^2 і скопіюйте їх у діапазон F3:G11.

4. Обчисліть суми величин ni, nіxі, nixi² у клітинках D12, F12 і G12, скориставшись функцією СУММА.

5. Визначте у клітинках Е15:Е16 середнє значення та стандартне відхилення за формулами (1)—(3). Ви маєте отримати такі значення, як на рис. 10.4.

6. Виходячи з отриманих значень середнього та стандартного відхилення, зробіть висновки щодо розподілу підприємств за величиною прибутку.

Вправа 3. Виявлення кореляційного зв'язку

Протягом року продовольча компанія здійснювала рекламу своєї продукції шляхом виготовлення та розповсюдження рекламних листівок у кількості від 89 000 до 345 000 шт. за місяць. По­трібно визначити, чи був цей захід ефективним та як вплине на дохід компанії виготовлення та розповсюдження протягом місяця 500 000 листівок.

1. Створіть нову електронну таблицю, введіть у неї дані, зазна­чені на рис. 10.9, і збережіть документ у файлі Вправа_3.хІs.

Оскільки нас цікавить залежність доходу від кількості поши­рених листівок, то кількість рекламних листівок є факторною ознакою, а дохід компанії — результативною.

2. Побудуйте для створеної таблиці точкову діаграму, скористав­шись кнопкою Майстер діаграм. На осі X має відображати­ся кількість листівок, на осі У — дохід компанії (рис. 10.10).

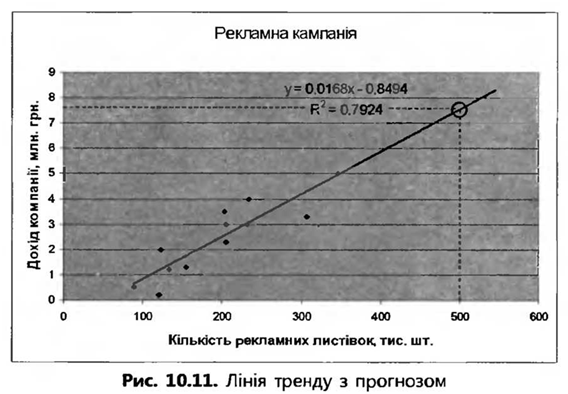
Як бачите, множина точок на діаграмі розсіювання витягнута зліва знизу вправо вверх. Це свідчить про існування пря­мого кореляційного зв’язку між кількістю розповсюджених рекламних листівок та доходом компанії.

3. Розрахуйте коефіцієнт кореляції, увівши в клітинку В6 фор­мулу =КОРРЕЛ(ВЗ:МЗ;В4:М4). Отримане значення коефіцієнта кореляції (0,89) підтверджує висновок про наявність сильного прямого лінійного кореляційного зв’язку між кількістю роз­повсюджених рекламних листівок та доходом компанії. Отже, рекламний захід можна вважати ефективним.

4. Додайте до точкової діаграми лінію тренду лінійного типу з відображенням регресійного рівняння та значення коефі­цієнта детермінації на діаграмі. Величину прогнозу вперед задайте рівною 200. Отримане значення R²= 0,7924 свідчить про те, що лінійна регресія достатньо добре відповідає вибір­ковим даним. Запишіть це значення у клітинці В7.

5. Перегляньте графік лінії тренду та визначте за ним, на який приблизно дохід компанії можна розраховувати в разі поши­рення 500 000 рекламних листівок за місяць (рис. 10.11).

6. Самостійно побудуйте поліноміальні лінії тренду другого і третього степенів. Порівняйте коефіцієнти детермінації та значення прогнозу для цих ліній тренду з відповідними зна­ченнями для лінійного тренду. Зробіть висновки.

Підсумок уроку.

Домашнє завдання.

1. Вивчити конспект.

2. Виконати завдання 3.

Урок 63

Ряд розподілу. Статистична залежність, коефіцієнт парної лінійної кореляції, кореляційна таблиця. Побудова інтервальних рядів розподілу. Побудова діаграм рядів розподілу. Побудова лінійної регресійної моделі. Обчислення коефіцієнтів парної лінійної регресії. Поняття кореляції статистичних показників. Розрахунок коефіцієнта кореляції за допомогою стандартної функції.

Мотивація.

У попередньому розділі ми досліджували вибірки, дані в яких були незгруповані, тобто являли собою просто послідовності чи­сел. За такою послідовністю можна обчислити певні статистичні показники, але неможливо визначити тенденцію зміни значень досліджуваної ознаки. Наприклад, якщо є відомості про доходи 1000 осіб, можна визначити середній дохід, стандартне відхилен­ня величини доходу, проте важко сказати, як змінюється кіль­кість осіб, що отримують той чи інший дохід, зі зростанням його величини.

Вивчення нового матеріалу.

Статистичні ряди розподілу

Щоб дати відповідь на це питання, потрібно згрупува­ти дані, наприклад визначити кількість людей, що отримують дохід до 1000 грн, від 1000 до 2000 грн, від 2000 до 3000 грн тощо. У результаті ми отримаємо таблицю на кшталт табл. 10.1.

Побудована таблиця називається статистичним рядом розподілу. Загалом ряд розподілу — це два набори значень однакової довжи­ни. В одному наборі представлені значення певноїознаки (у табл. 10.1 це величина доходу), а в іншому — частоти, тобто кількості разів, коли під час статистичного спостереження було отримано відповідне значення ознаки. Інакше кажучи, ідеться про розподіл певних об’єктів за певною ознакою. Наприклад, у табл. 10.1 на­ведено розподіл осіб за величиною доходу. Величина доходу — це ознака, а кількості осіб — частоти.

За рядом розподілу вже можна визначити тенденцію зміни зна­чень досліджуваної ознаки. Так, з табл. 10.1 видно, що з ростом доходу від 0 до 2000 грн кількість осіб, які отримують цей дохід, зростає, а коли дохід перевищує 2000 грн, тенденція зворотна: що вище дохід, то менша кількість людей його отримує.

Атрибутивні та варіаційні ряди розподілу

Розрізняють атрибутивні та варіаційні ряди розподілу. Якщо за основу групування узята якісна ознака, то це атрибутивний ряд розподілу (розподіл за видами продукції, професіями, статтю, на­ціональною або географічною приналежністю тощо). Якщо ряд розподілу побудований за кількісною ознакою, то такий ряд є варіаційним (за розміром доходу, стажем роботи, числом праців­ників на підприємстві тощо).

Наприклад, наведений у табл. 10.1 ряд розподілу осіб за доходом є варіаційним, а ряд розподілу осіб за професіями, який наведено у табл. 10.2, — атрибутивним.