Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы о вероятности произведения событий.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Определение. Условной вероятностью Р(В/А) называется вероятность события В при условии, что произошло некоторое событие А с положительной вероятностью, т.е. Р(А) Теорема 1 (о вероятности произведения). Р(АВ)=Р(А)Р(В/А). (5) Пример. В коробке 10 шаров: 4 белых и 6 черных. По-очереди извлекаются два шара. Найти вероятность того, что оба шара белые. Решение. Пусть А – событие: оба шара белые. Тогда А1 – событие: 1-ый шар белый, А2 – событие: 2-ой шар белый. Очевидно, что А=А1А2. Находим Р(А)=Р(А1А2)=Р(А1)Р(А2/А1) = Следствие. Вероятность произведения n событий равна произведению вероятности одного из них на условные вероятности всех остальных, вычисленные в предположении, что все предыдущие события наступили:
Замечание. В частности, для трех событий А, В, С формула (6) принимает вид:
Введем понятие независимости двух событий. Определение. Говорят, что событие В не зависит от события А, если Р(В)=Р(В/А). Справедливо следующее утверждение. Утверждение. Если событие В не зависит от события А, то и событие А не зависит от события В. При этом события А и В называют независимыми. Замечание. Отметим, что если А и В независимые, то независимы Теорема 2 (о вероятности независимых событий). Если события А и В независимые, то Р(АВ)=Р(А)Р(В). (8) Пример. В коробке 4 белых и 6 черных шаров. Два раза извлекают по одному шару и каждый раз кладут его обратно. Найти вероятность того, что оба раза вытащили белый шар. Решение. Пусть А – событие: оба раза вытащили белый шар. Тогда А1 – событие: 1-ый раз вытащили белый шар, А2 - событие: 2-ый раз вытащили белый шар. Очевидно, что А=А1А2, причем А1 и А2 независимые. Находим Р(А)=Р(А1А2)=Р(А1)Р(А2)= Замечание. Для трех независимых событий А, В, С формула (8) принимает вид: Р(АВС)=Р(А)Р(В)Р(С). (9) Определение. События А1, А2,…, Аk называются независимыми в совокупности, если любое из этих событий не зависит ни от какого произведения, составленного из остальных событий. Следствие. Если события А1, А2,…, Аk независимые в совокупности, то Р( Замечание. Вычисление вероятности суммы событий можно свести к вычислению вероятности произведения противоположных событий по формуле:
В частности, если события А1,А2,…,Аk независимы, то
Упражнения. 1. Мастер обслуживает 5 станков. 10% рабочего времени он проводит у первого станка, 15% - у второго станка, 20% - у третьего, 25% - у четвертого, 30% - у пятого. Найти вероятность того, что в наудачу выбранный момент времени он находится: 1) у первого или третьего станка; 2) у второго или пятого; 3) у первого или четвертого станка; 4) у третьего или пятого; 5) у первого или второго, или четвертого станка. Решение. Обозначим через А, В, С, D, Е – события,состоящие в том, что в наудачу выбранный момент времени мастер находится соответственно у первого, второго, третьего, четвертого, пятого станка. Из условия следует, что А, В, С, D, Е попарно несовместны и Принимая во внимание определение суммы событий и теорему сложения вероятностей несовместных событий, находим:
2. Слово папаха составлено из букв разрезной азбуки. Карточки с буквами тщательно перемешаны. Четыре карточки извлекаются по очереди и раскладываются в ряд. Какова вероятность получить таким путем слово папа? Решение. Обозначим через А, В, С, D соответственно события: извлечена первая, вторая, третья и четвертая буква слова папа из набора в 6 букв: а, а, а, п, п, х. Найдем вероятность событий: А, В/А, С/АВ, D/ABC.
В соответствии с формулой (6) при n=4 получаем
Формула полной вероятности Пусть событие А может произойти после наступления одного из событий H1, H2,…, Hm, причем события H1, H2,…, Hm образуют полную группу и попарно несовместны. Определение. События H1, H2,…, Hm называются гипотезами для события А. Справедлива следующая теорема. Теорема (формула полной вероятности). Пусть H1, H2,…, Hm – гипотезы для события А. Тогда P(A)=P(H1)P(A/H1)+P(H2)P(A/H2)+…+P(Hm)P(A/Hm) или (*) P(A) = Пример. В магазин поступают изделия с трех фабрик: 20% - с фабрики №1, 30% - с фабрики №2, 50% - с фабрики №3. Фабрика №1 допускает 1% брака, фабрика №2 допускает 2% брака, фабрика №3 допускает 0,5% брака. Случайным образом выбирается одно изделие. Найти вероятность того, что оно бракованное. Решение. Пусть А – событие: выбранное изделие бракованное. Через Hi обозначим события: изделие поступило с фабрики № i (i=1,2,3), причем H1, H2, H3 попарно несовместны. Тогда по формуле полной вероятности P(A)=P(H1)P(A/H1)+P(H2)P(A/H2)+Р(Н3)Р(А/Н3)= Упражнение. 1. В группе 21 студент, в том числе 5 отличников, 10 хорошо успевающих и 6 занимающихся слабо. На предстоящем экзамене отличники могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. Слабо занимающиеся студенты могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена приглашается наудачу один студент. Найти вероятность того, что он получит хорошую или отличную оценку (событие А). Решение. Обозначим гипотезы: Из условия задачи следует, что
По формуле (*) находим искомую вероятность P(A)=P(H1)P(A/H1)+P(H2)P(A/H2)+P(H3)P(A/H3)=
Формулы Байеса Пусть H1, H2,…, Hm – гипотезы для А. Предположим, что событие А уже произошло. Тогда вероятности гипотез, вообще говоря, меняются. Пример. Имеются две коробки с шарами. В 1-ой коробке содержится 99 белых шаров и 1 черный шар. Во 2-ой коробке содержится 1 белый шар и 99 черных шаров. Случайным образом выбирают коробку и достают один шар. Какова вероятность того, что это белый шар? Решение. Пусть А – событие: достали белый шар. Тогда Н1 – событие: выбрана коробка №1, Н2 – событие: выбрана коробка №2. Р(Н1)=Р(Н2)= Предположим, что событие А уже произошло. Тогда гипотеза Н1 более вероятна. Справедлива следующая теорема. Теорема (формулы Байеса). Пусть H1, H2,…, Hm – гипотезы для А. Тогда
Замечание. Вероятность Р(А) можно вычислить по формуле полной вероятности, поэтому формулы Байеса можно записать в виде:
Вернемсяк примеру из предыдущего параграфа (§6). Случайным образом выбирается одно изделие, которое оказалось бракованное. Найти вероятность того, что оно будет изготовлено на фабрике №1. Решение. Для ответа на вопрос задачи найдем Р(Н1/А). Для этого воспользуемся одной из формул Байеса:
Упражнение. 1. На складе находятся детали, изготовленные на двух заводах. Известно, что объем продукции первого завода в 4 раза превышает объем продукции второго завода. Вероятность брака на первом заводе Решение. Обозначим через
Пусть А – событие, состоящее в том, что наудачу взятая деталь оказалась бракованной. По условию
В соответствии с формулой (2) в случае m=2 получаем
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1181; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |



 (6)
(6) (7)
(7) и В, А и
и В, А и  ,
, 
 )=Р(А1)Р(А2)…Р(Аk). (10)
)=Р(А1)Р(А2)…Р(Аk). (10) . (11)
. (11) . (12)
. (12) ,
,  ,
, 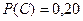 ,
,  ,
,  .
. ;
; ;
; ;
; ;
; .
.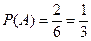 ;
;  ;
;  ;
;  .
. .
. .
.
 - «приглашен студент-отличник»,
- «приглашен студент-отличник»,  - «приглашен хороший студент»,
- «приглашен хороший студент»,  - «приглашен слабый студент».
- «приглашен слабый студент». ,
,  ,
,  ;
;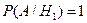 ,
,  ,
,  .
. .
.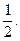 Тогда
Тогда  .
. (1)
(1) (2)
(2)
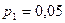 , на втором -
, на втором - 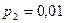 . Наудачу взятая деталь оказалась бракованной. Какова вероятность того, что эта деталь изготовлена первым заводом?
. Наудачу взятая деталь оказалась бракованной. Какова вероятность того, что эта деталь изготовлена первым заводом?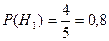 ,
,  .
. ,
,  .
.