
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция распределения случайной величиныСодержание книги
Поиск на нашем сайте
Определение. Функцией распределения случайной величины
Если в контексте неважно о какой величине идет речь или величина известна заранее, то будем использовать обозначение F(x). Пример. Бросается игральная кость. Случайная величина Решение. Рассмотрим следующие ситуации: 1) 2) 3) 4) 5) 6) 7)
Свойства функции распределения. 1. 2. 3. Функция распределения F(x) – неубывающая, т.е.
4. Функция распределения F(x)непрерывна слева в любой точке 5. Замечание. Если некоторая функция F(x) удовлетворяет свойствам 1-5, то эта функция является функцией распределения некоторой случайной величины. Дискретные случайные величины Определения Определение. Случайная величина Пусть случайная величина
Таблица такого вида называется таблицей распределения случайной величины Определение. Ряд Утверждение. Если последовательность {pn} такова, что Пример. Бросается монета до первого выпадения герба. Случайная величина
Найдем сумму ряда:
График функции распределения дискретной случайной величины:
Биномиальная случайная величина Определение. Дискретная случайная величина
Таблица распределения:
Покажем, что этот закон задает случайную величину. Найдем сумму ряда распределения: Закон действительно определяет случайную величину. Замечание. Биномиальную случайную величину можно трактовать как количество наступлений некоторого события А в схеме Бернулли из n испытаний, если Р(А)=р в каждом испытании:
Пуассоновская случайная величина Определение. Дискретная случайная величина Таблица распределения:
Покажем, что этот закон задает случайную величину. Найдем сумму ряда распределения: Закон Пуассона, как предельный для биномиального Пусть производится последовательность серий испытаний Бернулли. В серии №1 – одно испытание, в результате которого может произойти событие А с вероятностью р1. В серии №2 – два испытания, в результате которых может произойти событие А с вероятностью р2. И т.д. В серии №n – n испытаний, в результате которых может произойти событие А с вероятностью рn. И т.д. Справедлива следующая теорема. Теорема. Пусть для указанной последовательности серий испытаний существует такое число а, что npn=a. Тогда Замечание. Из теоремы вытекает, что при достаточно больших n: Примеры. 1) Из фабрики в магазин везут 5000 качественных изделий. Вероятность того, что в дороге изделие повредится, равна 0,0002. Найти вероятность того, что в дороге повредится три изделия. Решение. Воспользуемся законом Пуассона, как предельным для биномиального: 2) Вероятность попадания в цель при одном выстреле равна 0,001. Найти вероятность хотя бы одного попадания, если число выстрелов равно 5000. Решение. Пусть А – событие: будет хотя бы одно попадание. Найдем вероятность непопадания в цель, т.е.
Искомая вероятность
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.21.101 (0.005 с.) |

 называется действительная функция
называется действительная функция  , заданная на множестве R такая, что
, заданная на множестве R такая, что .
.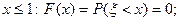










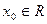 , т.е.
, т.е. 

 .
. Составим таблицу:
Составим таблицу: называется рядом распределения случайной величины
называется рядом распределения случайной величины 
 , то указанный ряд является рядом распределения некоторой случайной величины.
, то указанный ряд является рядом распределения некоторой случайной величины.



 Этот ряд является рядом распределения случайной величины
Этот ряд является рядом распределения случайной величины 
 и вероятность
и вероятность





 .
.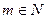 и вероятность
и вероятность 




 Закон действительно определяет случайную величину.
Закон действительно определяет случайную величину.
 , т.е. при достаточно больших n закон Пуассона можно трактовать, как предельный для биномиального (т.е. как количество наступлений события).
, т.е. при достаточно больших n закон Пуассона можно трактовать, как предельный для биномиального (т.е. как количество наступлений события).





