
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схема Бернулли независимых испытанийСодержание книги
Поиск на нашем сайте
Пусть производится серия из n испытаний. После каждого из этих испытаний с вероятностью p может произойти некоторое событие А. Причем вероятность не зависит ни от исхода предыдущих испытаний, ни от последующих. Такая серия испытаний называется схемой Бернулли независимых испытаний. Обозначим через Pn(m) вероятность того, что событие А в схеме Бернулли из n испытаний произошло ровно m раз. Тогда справедлива следующая формула (формула Бернулли): Pn(m)= Замечание. В дальнейшем число 1-р будем обозначать q, т.е. q=1-p. Тогда формула Бернулли примет вид: Pn(m)= Пример. Производится 10 выстрелов по мишени. Вероятность попадания при каждом выстреле 0,9. Найти вероятность того, что будет ровно 7 попаданий. Решение. В качестве испытания рассмотрим выстрел, в качестве события А – попадание в цель. Получим схему Бернулли из n=10 испытаний, р=0,9. Требуется найти P10(7): P10(7)= Упражнение. 1. Производится серия из 6 бросков монеты. Найти вероятность того, что «орел» выпадет ровно k раз (k=0,1,2,…,6). Решение. P6(0)= P6(1)= P6(2)= P6(3)= Наиболее вероятно, что «орел» выпадет 3 раза.
Интегральная и локальная формулы Муавра-Лапласа Схема Бернулли при большом количестве испытаний практически плохо применима. Кроме этого, на практике обычно важно знать не вероятность того, что событие произойдет ровно m раз, а вероятность того, что оно произойдет не меньше m1 раз и не больше m2 раз. Вероятность такого события будем обозначать: Обозначим через
где Кроме интегральной формулы существует еще и локальная формула Муавра-Лапласа:
где Замечание. Чем больше n, тем точнее формулы (*) и (**). Примеры. 1) Испытывается 100 приборов. Вероятность того, что прибор не пройдет испытание равна 0,2. Найти вероятность того, что испытание пройдет не менее 72 приборов. Решение. По условию n=100, p=0,2, q=0,8. Требуется найти вероятность того, что испытание не пройдет 28 или меньше приборов, т.е. Тогда
2) В некоторой местности из каждых 100 семей 80 имеют холодильники. Найти вероятность того, что из 400 семей 300 имеют холодильники. Решение. Вероятность того, что семья имеет холодильник, равна Замечание. Весьма малое значение вероятности Глава 3. Случайные величины
Предположим, что в результате испытания некоторая величина принимает какое-либо числовое значение. Такую величину будем называть случайной. Примеры. 1) Бросается игральный кубик. Случайная величина – выпавшая цифра. Множество значений: {1,2,3,4,5,6}. 2) Бросается монета до тех пор, пока не выпадет герб. Случайная величина – количество бросков. Множество значений: N. 3) Случайная величина, например, - время безотказной работы некоторого механизма. Множество значений: [0;∞). Первые два примера – это примеры дискретной случайной величины. Третий пример – непрерывной случайной величины. Определение. Пусть < Символически: В дальнейшем это множество будем обозначать ( Пример. Бросается игральный кубик. Случайная величина Если L – множество всех подмножеств Замечание. По аналогии с обозначением (
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 370; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.153.77 (0.006 с.) |

 . (1)
. (1) (2)
(2)
 [ p=q=1/2] =
[ p=q=1/2] =  =
=  P6(6);
P6(6);
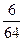 =
=  P6(5);
P6(5);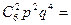
 =
=  P6(4);
P6(4);
 .
.
 , через
, через  Тогда
Тогда , (*)
, (*) - функция Лапласа. Функция Лапласа нечетная и монотонно возрастающая. Формула (*) называется интегральной формулой Муавра-Лапласа.
- функция Лапласа. Функция Лапласа нечетная и монотонно возрастающая. Формула (*) называется интегральной формулой Муавра-Лапласа. , (**)
, (**) Функция f(x) четная и монотонно убывающая.
Функция f(x) четная и монотонно убывающая.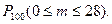
 В результате
В результате
 Т.к. n=400 достаточно велико (npq=64
Т.к. n=400 достаточно велико (npq=64 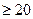 ), то
), то  Тогда
Тогда 
 не должно вызывать сомнения, т.к. кроме события «ровно 300 семей из 400 имеют холодильники» возможно еще 400 событий: «0 из 400», «1 из 400»,…, «400 из 400» со своими вероятностями. Все вместе эти события образуют полную группу, a значит, сумма их вероятностей равна 1.
не должно вызывать сомнения, т.к. кроме события «ровно 300 семей из 400 имеют холодильники» возможно еще 400 событий: «0 из 400», «1 из 400»,…, «400 из 400» со своими вероятностями. Все вместе эти события образуют полную группу, a значит, сумма их вероятностей равна 1. §1. Понятие случайной величины
§1. Понятие случайной величины > - некоторое вероятностное пространство. Случайной величиной, заданной на этом вероятностном пространстве, называется функция
> - некоторое вероятностное пространство. Случайной величиной, заданной на этом вероятностном пространстве, называется функция  , определенная на множестве
, определенная на множестве  со значениями во множестве R такая, что для любого х
со значениями во множестве R такая, что для любого х  R множество всех элементарных событий
R множество всех элементарных событий  , для которых
, для которых 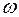 )< х, является элементом из L.
)< х, является элементом из L. .
. ), (
), (


