
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 1. Элементы комбинаторикиСодержание книги
Поиск на нашем сайте Теория вероятностей Семестр Преподаватель: Н.В. Горбунова. Введение Задача любой науки, в том числе экономической, состоит в выявлении и исследовании закономерностей, которым подчиняются реальные процессы. Найденные закономерности, относящиеся к экономике, имеют не только теоретическую ценность, они широко применяются на практике - в планировании, управлении и прогнозировании. Теория вероятностей - математическая наука, изучающая закономерности случайных явлений. Под случайными явлениями понимаются явления с неопределенным исходом, происходящие при неоднократном воспроизведении определенного комплекса условий. Теория вероятностей возникла в 17 веке в работах Паскаля, Ферма и Гюйгенса, причем ее первоначальное развитие связано с исследованием азартных игр. Действительно, карты, рулетка, игральные кости, различные лотереи издавна привлекали внимание определенных кругов общества. Одним они обеспечивали возможность скоротать время, других обогащали, третьих разоряли, давая немало поводов поговорить о случайных событиях и их вероятностях. Но в тот далекий от нас период, который относится к предыстории теории вероятностей, было немало и других проблем, в частности проблемы демографии и страхования. Эти и другие проблемы вызывали потребность в специальной науке в гораздо большей мере, чем азартные игры. Важный этап в развитии теории вероятностей связан с именем Я. Бернулли. Работы Бернулли во многом определи дальнейшее развитие этой науки. Они стимулировали, в частности, исследования Муавра, Лапласа, Гаусса, Пуассона. Очередной этап в развитии теории вероятностей тесно связан с Петербургской школой, видными представителями которой были Чебышев, Марков, Ляпунов. Их усилиями были значительно расширены области применения предельных теорем, которые ныне именуются законом больших чисел и центральной предельной теоремой и составляет основу теории вероятностей. В настоящее время теория вероятностей - наука, без которой не обходится ни физика, ни астрономия, ни экономика, ни биология, ни лингвистика. Она находит применение практически везде. Кроме того, в последнее время теория вероятностей стала основой развития многих новых научных направлений, таких, как математическая статистика, теория информации, теория массового обслуживания.
Упражнения. Из цифр 1,2,3,4,5 составляются всевозможные пятизначные числа без повторяющихся цифр. 1) Сколько всего получится таких чисел? 2) Сколько среди них будет начинаться с цифры 5? 3) Сколько чисел будет оканчиваться комбинацией 41? 4) Сколько получится четных и нечетных чисел? 5) Сколько получится чисел, кратных 3? Решение. 1) Всего пятизначных чисел будет 2) Так как числа начинаются с 5, то на остальных четырех позициях могут располагаться числа 1, 2, 3, 4. Количество таких расположений: 3) Чисел, оканчивающихся комбинацией 41, будет столько, сколько существует способов расположения в ряд «остальных» цифр 2, 3, 5, т.е. 3!=6. 4) Четные из рассматриваемых цифр оканчиваются либо цифрой 2, либо цифрой 4. И тех и других будет 5) Для того, чтобы числа были кратные 3 нужно, чтобы они оканчивались 3. Их будет столько, сколько существует способов расположения в ряд цифр 1, 2, 4, 5, т.е. Выборки с повторениями Пусть имеется n сортов каких-либо объектов. Определение. Выборкой с повторениями длины m называется любой набор, состоящий из m штук объектов произвольных сортов (m может быть больше n). Любой объект одного сорта будем обозначать одним символом (a, b,…) и называть элементом. Пусть некоторый элемент a входит в выборку k раз, т.е. в выборке присутствует k объектов одного сорта. При этом будем говорить, что элемент a имеет кратность k. Определение. Размещениями с повторениями из n по m элементов называются такие выборки с повторениями длины m, которые различаются либо элементами, либо их кратностями, либо их порядком. Количество всех таких размещений обозначается
Пример. Сколькими способами можно составить трехзначные числа из цифр 1,2,3,4? Решение. Любое такое число есть размещение с повторениями из 4 по 3. Их количество: Определение. Выборки, состоящие из m элементов кратности k1, k2, …, kp соответственно и отличающиеся только порядком элементов, называются перестановками из m элементов кратности k1, k2,…, kp (k1+k2+…+kp=m, m – длина выборки). Количество всех таких перестановок обозначается
Пример. Сколькими способами можно разместить лампочки в гирлянде, состоящей из 11 лампочек: 4 красных и 7 зеленых? Решение. Любой способ – перестановка с повторениями из 2-х элементов кратности 4 и 7. Их количество равно: Определение. Сочетаниями с повторениями из n по m элементов называются такие выборки с повторениями длины m, которые отличаются либо элементами, либо их кратностями. Количество таких сочетаний обозначается
Пример. В цветочном киоске имеются цветы 3-х сортов. Сколькими способами можно составить различные букеты, состоящие из 5 цветов? Решение. Любой букет – сочетание с повторениями из 3 по 5. Их количество: Упражнения. 1. Сколькимиспособами можно насадить на нить 3 красных, 7 зеленых и 4 синих бусинки? Решение. Бусинки можно насадить на нить 2. Сколькими способами можно выбрать 5 шахматных фигур из 32? Решение. Количество способов выбора шахматных фигур равно
Бином Ньютона Определение. Формула
Называется формулой бинома Ньютона, а коэффициенты Формулу бинома Ньютона записывают также в следующем виде:
Возможна и другая запись:
Примеры. 1) Известные тождества:
2)
Биномиальные коэффициенты иногда располагают в виде так называемого треугольника Паскаля:
..……………………….... или, более определенно, 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 ….………………….. Треугольник Паскаля наводит на следующие свойства биномиальных коэффициентов. 10. Крайние члены треугольника Паскаля равны 1. Каждый же из остальных членов равен сумме двух смежных с ним членов, стоящих в предыдущей строке. Например (см. строку с номером n=4), 4=1+3, 6=3+3, 4=3+1. В общем случае (при 20. Члены всякой строки треугольника Паскаля сначала возрастают (до середины строки), а затем – убывают. Например, 1<4<6, 6>4>1 (четвертая строка). 30. Всякая строка треугольника Паскаля симметрична относительно своей середины (или: члены всякой строки треугольника Паскаля, равноудаленные от краев, равны между собой). Это свойство записывается в виде равенства:
40. Сумма членов n- ой строки треугольника Паскаля равна 2n:
Замечание. Это равенство можно рассматривать как следствие формулы бинома Ньютона при a=b=1. 50. Всякое непустое множество имеет столько подмножеств с четным числом элементов, сколько и подмножеств с нечетным числом элементов; иными словами, при
Пример. Сколько подмножеств имеет множество {1,2,…,10}, состоящее из 10 первых членов натурального ряда? Сколько из них содержит ровно три элемента? Решение. Для ответа на 1-ый вопрос задачи воспользуемся 40 свойством:
где Подмножеств, содержащих ровно три элемента будет Упражнения. 1. Вычислите: Решение. Данная формула – формула бинома Ньютона, где a=2, b=3, m=5. Тогда (a+b)n=(2+3)5=55=3125. 2. Найдите коэффициент при x3 многочлена Решение. Преобразуем многочлен
Глава 2. Случайные события События и действия над ними Определение. Опытом, или испытанием, называют всякое осуществление определенного комплекса условий или действий, при которых происходит соответствующее явление. Определение. Событие – понятие первичное, т.е. неопределяемое. Его можно представить как некоторый факт, который может произойти или не произойти в результате испытаний (опытов, экспериментов). Пример. 1) Попадание в цель при выстреле. Испытание – выстрел. Событие – попадание в цель. 2) Выпадение четной цифры при бросании игральной кости. Испытание – бросок. Событие – выпадение четной цифры. Все события можно разделить на 3 группы: 1. Достоверные события. Они всегда наступают в результате испытания. Пример. Раздается 33 карты из колоды в 36. Наличие туза – достоверное событие. 2. Невозможные события. Они никогда не наступают в результате испытания. Пример. Выпадение цифры 0 при бросании игральной кости. 3. Все остальные события – случайные. Они могут, как наступать так и не наступать в результате испытания. Примеры. 1) Наличие туза при раздаче 32 карт – случайное событие. 2) Выпадение цифры 1 (2,3,4,5,6) при бросании игральной кости – случайное событие. События обозначаются большими латинскими буквами: A,B,C,…. Через U будем обозначать достоверные события, через V – невозможные события. Дадим некоторые определения и введем действия над событиями. Определение. Каждое событие, которое может наступить в итоге опыта, называется элементарным событием (элементарным исходом, или шансом). Пример. События А1, А2, А3, А4, А5, А6 – элементарные события при подбрасывании игрального кубика. Определение. Говорят, что событие A благоприятствует событию B (при этом пишут Пример. Бросается игральная кость. Событие А: выпадение четной цифры, событие В: выпадение цифры 4. Определение. Говорят, что событие А эквивалентно (равно) событию В (при этом пишут А=В), если событие А благоприятствует событию В и событие В благоприятствует событию А одновременно (т.е. Пример. Бросается игральная кость. Событие А: выпадение цифры 5, событие В: выпадение нечетной цифры, большей 3. А=В. Определение. Суммой событий А и В (при этом пишут А+В) называется такое событие, которое заключается в наступлении хотя бы одного события А или В. Пример. Бросается игральная кость. Событие А: выпадение цифры 2 или цифры 4, событие В: выпадение цифры 2 или цифры 6. Событие А+В: выпадение четной цифры. Замечание. Сумму событий называют также объединением событий и обозначают Определение. Произведением событий А и В (при этом пишут Пример. Событие А: выпадение цифры меньшей 4, событие В: выпадение цифры нечетной. Событие Замечания. 1. В обозначении произведения точку можно опускать. 2. Если в выражении присутствует сумма и произведение, то произведение производится в первую очередь (если нет скобок). 3. Произведение событий называется также пересечением и обозначается Свойства суммы и произведения событий: 1) А+В=В+А (коммутативность сложения); 2) (А+В)+С=А+(В+С) (ассоциативность сложения); 3) АВ+ВА (коммутативность умножения); 4) (АВ)С=А(ВС) (ассоциативность умножения); 5) (А+В)С=АС+ВС (дистрибутивность сложения относительно умножения) Определение. События Пример. Бросается игральная кость.Событие А1: выпадение четной цифры, событие А2: выпадение цифры большей 2, событие А3: выпадение цифры 1. События А1, А2, А3 образуют полную группу. Определение. События А и В называются несовместными, если АВ=V, т.е. события А и В одновременно наступить не могут. Пример. Бросается игральная кость. Событие А: выпадение четной цифры, событие В: выпадение цифры 3. События А и В несовместны. Определение. Событие Замечание. События А и Пример. Бросается игральная кость. Событие А: выпадение четной цифры, событие Упражнения. 1. Образуют ли полную группу следующая группа событий: опыт – вынимание карты из колоды; события: А1 – появление карты червонной масти; А2 – появление карты бубновой масти; А3 – появление карты трефовой масти? (Ответ: нет). 2. Являются ли несовместными следующие события: опыт – бросание двух монет; события: В1 – появление решки на первой монете; В2 – появление цифры на второй монете? (Ответ: нет).
Примеры. 1) Бросается монета. Пусть событие А: выпадение орла, событие В: выпадение решки. События А и В – равновероятны. 2) Бросается игральный кубик. Событие А1: выпадение цифры 1, событие А2: выпадение цифры 2, событие А3: выпадение цифры 5. События А1, А2, А3 – равновероятны. Определение. События Е1,Е2,…,Еn образуют группу элементарных событий, если: 1) События Е1,Е2,…,Еn равновероятны. 2) События Е1,Е2,…,Еn образуют полную группу событий. 3) События Е1,Е2,…,Еn попарно несовместны, т.е. для любых Определение. События Е1,Е2,…,Еn называются элементарными событиями. Пусть событие А равно сумме m штук элементарных событий из множества {Е1,Е2,…,Еn}. Определение. Классической вероятностью события А называется число равное Обозначается: Р(А). Замечание. Р – первая буква франц. слова probabilite’ – вероятность). В дальнейшем m будем обозначать mA. Таким образом, Р(А)= где mA – количество элементарных событий, образующих в сумме событие А (или количество элементарных событий, благоприятствующих наступлению события А), n – общее количество элементарных событий. Примеры. 1) Найти вероятность того, что при бросании игральной кости выпадет число большее 4. Решение. Пусть А – событие: выпадет цифра большая 4. Пусть Еi – события: выпадет цифра под номером i. Тогда E1, E2, E3, E4, E5, E6 образуют группу элементарных событий. Количество всех элементарных событий n =6. А=Е5+Е6. Тогда mA =2 и Р(А) = 2) Найти вероятность того, что при бросании игральной кости выпадет число меньшее 4. Решение. Пусть А – событие: выпадет цифра меньшая 4. Пусть Еi – события: выпадет цифра под номером i. Тогда E1, E2, E3, E4, E5, E6 образуют группу элементарных событий. Количество всех элементарных событий n =6. А=Е1+Е2+Е3. Тогда mA =3 и Р(А) = 2-ой способ. Пусть событие Е1: выпадение цифр 1,2,3,событие Е2: выпадение цифр 4,5,6.Тогда Е1 и Е2 образуют группу элементарных событий. Их количество n =2. Событие А=Е1, mA =1, Р(А)= 1/2. 3) Найти вероятность того, что играя в лотерею «5 из 35» одним билетом угадаем все 5 номеров. Решение. Пусть А – событие: билет окажется выигрышным. В качестве элементарного события возьмем выпадение каких-либо 5 различных чисел от 5 до 35. Количество всех элементарных событий n = 4) В партии состоящей из N деталей, М штук бракованных. Случайным образом выбираются k деталей. Найти вероятность того, что среди них ровно l бракованных. Решение. Пусть А – событие: среди k деталей ровно l деталей бракованных. Элементарные события – набор из k деталей. Их количество
Выбор оставшихся бракованных изделий наборов из небракованных изделий Тогда Свойства вероятностей: 1) Р(U)=1. Доказательство. По определению U=E1+E2+…+En. Тогда mU=n; Р(U)= 2) P(V)=0. Доказательство. Т.к. mV=0, то P(V)= 3) Доказательство. Пусть А – любое событие. Тогда 4) Доказательство. Т.к.
Пример. Отдельные тома некоторого пятитомного издания располагаются на книжной полке в случайном порядке. Какова вероятность того, что хотя бы один том окажется не на своем месте? Решение. Пусть А – событие: хотя бы один том окажется не на своем месте. Тогда Упражнения. 1. Группа из k человек(k >2) случайным образом рассаживаются за круглым k -местным столом. Найти вероятность того, что два определённых лица X и Y окажутся рядом. Решение. 1-ый способ. Пусть А – событие: два лица X и Y окажутся рядом. Элементарные события – размещение k человек. Их количество 2-ый способ. Элементарные события – посадка X и Y; 2. Набирая номер телефона, абонент забыл три последние цифры. Вспомнив, что они все различные он набрал их наугад. Найти вероятность того, что он попал по нужному адресу. Решение. Пусть А – событие: набраны три нужные цифры (или угадан номер телефона). Элементарные события – упорядоченный набор из трех различных цифр. Их количество
Геометрические вероятности Классическое определение вероятности предполагает, что число элементарных событий конечно. На практике встречаются опыты, для которых множество таких событий бесконечно. Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом событий, вводят геометрические вероятности – вероятности попадания точки в область. Пусть в область
Определение. Вероятность попадания точки в область g равна отношению площадей областей g и G, т.е. Р(А)= где S – площадь соответствующей области. Замечание 1. Аналогично вводится понятие геометрической вероятности при бросании точки в пространственную область G объема Р(А)= Замечание 2. Это определение можно распространять на любое пространство Р(А) = где mes – мера соответствующей области (mes- три буквы франц. слова mesure, что означает мера). Пример. Два лица X и Y договорились о встрече с 1200 до 1300 в определенном месте. Пришедший первым ждет 20 минут и уходит. Найти вероятность того, что они встретятся. Решение. Обозначим через А – событие: лица X и Y встретятся. Пусть x – время прихода лица X, измеряемое в минутах,
то точка (x; y) случайным образом попадает в область, которая задается данной системой. Обозначим ее G (это будет квадрат). По условию лица встретятся, если
Фигуру, заданную этой системой в пересечении с G обозначим g. Искомая вероятность: Р(A)= Упражнение. 1. В шар вписан куб. Точка наудачу зафиксирована в шаре. Найти вероятность того, что точка попадет в куб. Решение. Введем обозначения: Событие А – «попадание точки в куб»; R – радиус шара, а – ребро куба, V – объем шара, V1 – объем вписанного куба. Как известно,
Упражнение. 1. Среди 300 деталей, изготовленных на автоматическом станке, оказалось 15, не отвечающих стандарту. Найти частоту появления нестандартных деталей. Решение. В данном случае n= 300, m= 15, поэтому
Упражнения. 1. Мастер обслуживает 5 станков. 10% рабочего времени он проводит у первого станка, 15% - у второго станка, 20% - у третьего, 25% - у четвертого, 30% - у пятого. Найти вероятность того, что в наудачу выбранный момент времени он находится: 1) у первого или третьего станка; 2) у второго или пятого; 3) у первого или четвертого станка; 4) у третьего или пятого; 5) у первого или второго, или четвертого станка. Решение. Обозначим через А, В, С, D, Е – события,состоящие в том, что в наудачу выбранный момент времени мастер находится соответственно у первого, второго, третьего, четвертого, пятого станка. Из условия следует, что А, В, С, D, Е попарно несовместны и Принимая во внимание определение суммы событий и теорему сложения вероятностей несовместных событий, находим:
2. Слово папаха составлено из букв разрезной азбуки. Карточки с буквами тщательно перемешаны. Четыре карточки извлекаются по очереди и раскладываются в ряд. Какова вероятность получить таким путем слово папа? Решение. Обозначим через А, В, С, D соответственно события: извлечена первая, вторая, третья и четвертая буква слова папа из набора в 6 букв: а, а, а, п, п, х. Найдем вероятность событий: А, В/А, С/АВ, D/ABC.
В соответствии с формулой (6) при n=4 получаем
Формула полной вероятности Пусть событие А может произойти после наступления одного из событий H1, H2,…, Hm, причем события H1, H2,…, Hm образуют полную группу и попарно несовместны. Определение. События H1, H2,…, Hm называются гипотезами для события А. Справедлива следующая теорема. Теорема (формула полной вероятности). Пусть H1, H2,…, Hm – гипотезы для события А. Тогда P(A)=P(H1)P(A/H1)+P(H2)P(A/H2)+…+P(Hm)P(A/Hm) или (*) P(A) = Пример. В магазин поступают изделия с трех фабрик: 20% - с фабрики №1, 30% - с фабрики №2, 50% - с фабрики №3. Фабрика №1 допускает 1% брака, фабрика №2 допускает 2% брака, фабрика №3 допускает 0,5% брака. Случайным образом выбирается одно изделие. Найти вероятность того, что оно бракованное. Решение. Пусть А – событие: выбранное изделие бракованное. Через Hi обозначим события: изделие поступило с фабрики № i (i=1,2,3), причем H1, H2, H3 попарно несовместны. Тогда по формуле полной вероятности P(A)=P(H1)P(A/H1)+P(H2)P(A/H2)+Р(Н3)Р(А/Н3)= Упражнение. 1. В группе 21 студент, в том числе 5 отличников, 10 хорошо успевающих и 6 занимающихся слабо. На предстоящем экзамене отличники могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. Слабо занимающиеся студенты могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена приглашается наудачу один студент. Найти вероятность того, что он получит хорошую или отличную оценку (событие А). Решение. Обозначим гипотезы: Из условия задачи следует, что
По формуле (*) находим искомую вероятность P(A)=P(H1)P(A/H1)+P(H2)P(A/H2)+P(H3)P(A/H3)=
Формулы Байеса Пусть H1, H2,…, Hm – гипотезы для А. Предположим, что событие А уже произошло. Тогда вероятности гипотез, вообще говоря, меняются. Пример. Имеются две коробки с шарами. В 1-ой коробке содержится 99 белых шаров и 1 черный шар. Во 2-ой коробке содержится 1 белый шар и 99 черных шаров. Случайным образом выбирают коробку и достают один шар. Какова вероятность того, что это белый шар? Решение. Пусть А – событие: достали белый шар. Тогда Н1 – событие: выбрана коробка №1, Н2 – событие: выбрана коробка №2. Р(Н1)=Р(Н2)= Предположим, что событие А уже произошло. Тогда гипотеза Н1 более вероятна. Справедлива следующая теорема. Теорема (формулы Байеса). Пусть H1, H2,…, Hm – гипотезы для А. Тогда
Замечание. Вероятность Р(А) можно вычислить по формуле полной вероятности, поэтому формулы Байеса можно записать в виде:
Вернемсяк примеру из предыдущего параграфа (§6). Случайным образом выбирается одно изделие, которое оказалось бракованное. Найти вероятность того, что оно будет изготовлено на фабрике №1. Решение. Для ответа на вопрос задачи найдем Р(Н1/А). Для этого воспользуемся одной из формул Байеса:
Упражнение. 1. На складе находятся детали
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 781; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.214.139 (0.013 с.) |

 .
. . Столько же будет и чисел, начинающихся цифрой 5.
. Столько же будет и чисел, начинающихся цифрой 5. , всего 48 чисел. Остальные числа будут нечетными; их количество может быть найдено как
, всего 48 чисел. Остальные числа будут нечетными; их количество может быть найдено как  или как
или как  (4! чисел, оканчивающихся цифрой 1, столько же – цифрой 3 и столько же – цифрой 5).
(4! чисел, оканчивающихся цифрой 1, столько же – цифрой 3 и столько же – цифрой 5). и равно:
и равно: . (1)
. (1)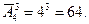
 и равно:
и равно: (2)
(2)
 и равно:
и равно: . (3)
. (3) =
= 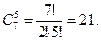
 способами.
способами. =
= 
 где
где 
 - биномиальные коэффициенты.
- биномиальные коэффициенты. .
. .
.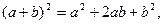
 .
.











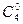










 )
) 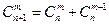 . Эта формула несет в себе правило построения каждой последующей строки треугольника Паскаля по предыдущей строке.
. Эта формула несет в себе правило построения каждой последующей строки треугольника Паскаля по предыдущей строке. .
.
 :
:

 - количество подмножеств, не содержащих ни одного элемента. Такое множество одно (
- количество подмножеств, не содержащих ни одного элемента. Такое множество одно ( ). Количество подмножеств, содержащих всего лишь один элемент – десять (
). Количество подмножеств, содержащих всего лишь один элемент – десять ( ). И т.д. Количество подмножеств, содержащих десять элементов – десять (
). И т.д. Количество подмножеств, содержащих десять элементов – десять ( ).
).
 .
. .
. . Воспользуемся формулой бинома Ньютона:
. Воспользуемся формулой бинома Ньютона: . Тогда коэффициент при x3:
. Тогда коэффициент при x3: 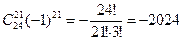 .
. ), если при наступлении события А обязательно наступает событие В.
), если при наступлении события А обязательно наступает событие В. . Обратное неверно.
. Обратное неверно. .
. ) называется такое событие, которое заключается в одновременном наступлении события А и события В.
) называется такое событие, которое заключается в одновременном наступлении события А и события В. .
. образуют полную группу событий, если
образуют полную группу событий, если  , т.е. хоты бы одно из событий
, т.е. хоты бы одно из событий  называется противоположным к событию А, если
называется противоположным к событию А, если  , т.е. одновременно события А и
, т.е. одновременно события А и  - взаимнопротивоположные.
- взаимнопротивоположные.
 i,j=1,2,…,n (никакие два события Е1,Е2,…,Еn не могут наступить одновременно).
i,j=1,2,…,n (никакие два события Е1,Е2,…,Еn не могут наступить одновременно). .
. ,
, .
. .
. . Событие А само является элементарным событием. Тогда mA =1 и Р(А) =
. Событие А само является элементарным событием. Тогда mA =1 и Р(А) =  0,000003.
0,000003. ;
; .
. .
.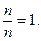

 , где А – любое событие.
, где А – любое событие.
 .
. , то
, то
 =5!=120. Тогда Р(
=5!=120. Тогда Р( , а Р(А)=1- Р(
, а Р(А)=1- Р(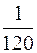 =
=  .
. ;
;  (Т.к. двух лиц X и Y можно посадить рядом двумя способами; остальных
(Т.к. двух лиц X и Y можно посадить рядом двумя способами; остальных  способами). Тогда
способами). Тогда  .
. ,
,  .
.  . (Лицо X садится куда угодно, тогда для Y остается k-1 место,
. (Лицо X садится куда угодно, тогда для Y остается k-1 место,  ).
). ;
;  . Тогда
. Тогда  .
. случайным образом брошена точка, область
случайным образом брошена точка, область  и пусть А – событие:попадание брошенной точки в область g.
и пусть А – событие:попадание брошенной точки в область g.
 ,
, , содержащую область g объема
, содержащую область g объема  :
: .
. . Тогда в качестве аналитической вероятности принимают следующую вероятность:
. Тогда в качестве аналитической вероятности принимают следующую вероятность: ,
, .Пусть y – время прихода лица Y, также измеряемое в минутах,
.Пусть y – время прихода лица Y, также измеряемое в минутах,  . Тогда пара (x; y) характеризует время прихода лиц X и Y. Эту пару можно интерпретировать как точку на координатной плоскости. Т.к.
. Тогда пара (x; y) характеризует время прихода лиц X и Y. Эту пару можно интерпретировать как точку на координатной плоскости. Т.к. ,
,

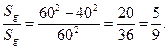
 ; поскольку V1=а3 и
; поскольку V1=а3 и  , то
, то  . В соответствии с формулой Р(А)=
. В соответствии с формулой Р(А)=  , приняв
, приняв  .
. .
. ,
,  ,
, 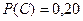 ,
,  ,
,  .
. ;
; ;
; ;
; ;
; .
.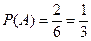 ;
;  ;
;  ;
;  .
. .
. .
.
 - «приглашен студент-отличник»,
- «приглашен студент-отличник»,  - «приглашен хороший студент»,
- «приглашен хороший студент»,  - «приглашен слабый студент».
- «приглашен слабый студент». ,
,  ,
,  ;
;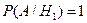 ,
,  ,
,  .
. .
.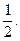 Тогда
Тогда  .
. (1)
(1) (2)
(2)



