
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 1. Случайные события. Вероятность событияСодержание книги
Поиск на нашем сайте
Условия вариантов задачи Ниже приведены 40 вариантов задачи 1. Номер варианта задачи, которую студент должен решить, указан в индивидуальном задании.
В задачах 1.1-1.5 подбрасываются две игральные кости. 1.1. Определить вероятность того, что сумма выпавших чисел равна восьми. 1.2. Определить вероятность того, что сумма выпавших чисел делится без остатка на шесть. 1.3. Определить вероятность того, что сумма выпавших чисел превышает 10. 1.4. Определить вероятность того, что выпадут одинаковые числа. 1.5. Определить вероятность того, что выпадут разные, но четные числа. 1.6. В урне четыре белых и пять черных шаров. Из урны наугад вынимают два шара. Найти вероятность того, что один из этих шаров - белый, а другой - черный. 1.7. В урне четыре белых и пять черных шаров. Из урны наугад вынимают два шара. Найти вероятность того, что оба шара будут одинакового цвета. 1.8. На десяти карточках написаны буквы А, А, А, М, М, Т, Т, Е, И, К. После перестановки вынимают наугад одну карточку за другой и раскладывают их в том порядке, в каком они были вынуты. Найти вероятность того, что на карточках будет написано слово “математика”. 1.9. Телефонный номер состоит из шести цифр, каждая из которых равновозможно принимает значения от 0 до 9. Найти вероятность того, что все цифры одинаковы. 1.10. Условие задачи 1.9. Вычислить вероятность того, что все цифры четные. 1.11. Условие задачи 1.9. Вычислить вероятность того, что номер не содержит цифры пять. 1.12. Условие задачи 1.9. Вычислить вероятность того, что все цифры различные и расположены в порядке возрастания (соседние цифры отличаются на 1). В задачах 1.13-1.19 наудачу взяты два положительных числа x и y, причем x £ 5, y £ 2. Найти вероятность того, что y+ax-b £ 0 и y-cx £ 0. 1.13. a=1, b=5, c=1. 1.14. a=1, b=5, c=0,5. 1.15. a=1, b=5, c=0,25. 1.16. a=1, b=5, c=2. 1.17. a=2, b=10, c=2. 1.18. a=2, b=10, c=1. 1.19. a=2, b=10, c=0,5. В задачах 1.20-1.23 из колоды в 36 карт (6, 7, 8, 9, 10, В, Д, К, Т) наугад извлекаются три карты. 1.20. Определить вероятность того, что будут вытащены карты одной масти. 1.21. Определить вероятность того, что будут вытащены три туза. 1.22. Определить вероятность того, что будут вытащены карты разных мастей. 1.23. Определить вероятность того, что среди извлеченных карт не будет 9. 1.24. На плоскости проведены параллельные прямые, находящиеся друг от друга на расстоянии 8 см. Определить вероятность того, что наугад брошенный на эту плоскость круг радиусом 3 см не будет пересечен ни одной линией.
1.25. В урне пять белых и восемь черных шаров. Из урны вынимают наугад один шар и откладывают в сторону. Этот шар оказался белым. После этого из урны берут еще один шар. Найти вероятность того, что этот шар тоже будет белым. В задачах 1.26-1.30 номер автомобиля содержит четыре цифры, каждая из которых равновозможно принимает значения от 0 до 9 (возможен номер 0000). 1.26. Определить вероятность того, что вторая цифра номера равна четырем. 1.27. Определить вероятность того, что номер содержит хотя бы одну цифру 0. 1.28. Определить вероятность того, что первые три цифры номера равны пяти. 1.29. Определить вероятность того, что номер делится на 20. 1.30. Определить вероятность того, что номер не содержит цифры 2. 1.31. В урне 6 белых и 7 черных шаров. Из урны вынимают шар – отмечается его цвет и он возвращается в урну, после этого вынимают второй шар. Найти вероятность того, что шары будут разных цветов. 1.32. Условие задачи 1.31. Найти вероятность, что шары будут белые. 1.33. Условие задачи 1.31. Найти вероятность, что шары будут одинакового цвета. 1.34. В урне 3 белых и 7 черных шаров. Из урны вынимают сразу 6 шаров. Найти вероятность того, что среди 6-и вынутых шаров будут 2 белых и 4 черных. 1.35. Условие задачи 1.34. Найти вероятность того, что все шесть шаров черные. 1.36. Телефонный номер состоит из шести цифр, каждая из которых равновозможно принимает значения от 0 до 9. Найти вероятность того, что случайно набранный номер оканчивается на 123. 1.37. Телефонный номер состоит из шести цифр, каждая из которых равновозможно принимает значения от 0 до 9. Найти вероятность того, что случайно набранный номер оканчивается на 444. 1.38. Проводится залп из трех орудий по цели. Вероятности попадания в цель из первого орудия 0,4, из второго – 0,7, из третьего – 0,9. Найти вероятность хотя бы одного попадания в цель. 1.39. Условие задачи 1.38. Найти вероятность того, что попало третье орудие, а 1 и 2 не попали. 1.40. Условие задачи 1.38. Найти вероятность того, что попало первое орудие, а 2 и 3 не попали.
Методические указания Случайное событие – любой факт в опыте со случайным исходом, который может произойти или не произойти. Любое случайное событие А, возможное в данном опыте, есть некоторое подмножество универсального множества
Событие А называется достоверным, если Событие А называется невозможным, если Противоположным событием Суммой или объединением двух событий А и В (обозначается Произведением или пересечением двух событий А и В (обозначается Несовместными событиями А и В называются такие, которые не могут произойти одновременно в одном опыте. Для несовместных событий Аксиома 1. Вероятность p(А) случайного события А есть функция множества элементарных исходов, благоприятных событию А, и вероятность любого события принимает значения
причем Аксиома 2. Вероятность суммы несовместных случайных событий равна сумме вероятностей этих событий:
Следствие аксиом 1 и 2: Вероятность прямого события
Классическое определение вероятности: вероятность события А определяется по формуле
где n – число всех возможных, равновероятных исходов данного опыта; m – число исходов, благоприятствующих появлению события. Геометрическое определение вероятности. Пусть в некоторую область случайным образом бросается точка T, причем все точки области равноправны в отношении попадания точки T.
Рис. 1.1 Тогда за вероятность попадания точки T в область A принимается отношение
где S (A) и S () — геометрические меры (длина, площадь, объем и т.д.) областей A и соответственно.
|
||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 335; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.11.13 (0.011 с.) |

 исходов этого опыта.
исходов этого опыта. , т.е. происходит в каждом опыте.
, т.е. происходит в каждом опыте. , т.е. никогда не происходит в данном опыте.
, т.е. никогда не происходит в данном опыте. называется событие, которое происходит тогда, когда не происходит событие А.
называется событие, которое происходит тогда, когда не происходит событие А. ) называется событие, состоящее в появлении или события А, или событии В, или А и В одновременно.
) называется событие, состоящее в появлении или события А, или событии В, или А и В одновременно. ) называется событие, состоящее в появлении и события А, и события В одновременно или совместно.
) называется событие, состоящее в появлении и события А, и события В одновременно или совместно. .
. , (1.1)
, (1.1) .
. (1.2)
(1.2)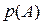 и вероятность противоположного события
и вероятность противоположного события  связаны соотношением
связаны соотношением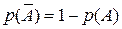 . (1.3)
. (1.3) , (1.4)
, (1.4)
 , (1.5)
, (1.5)


