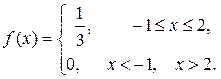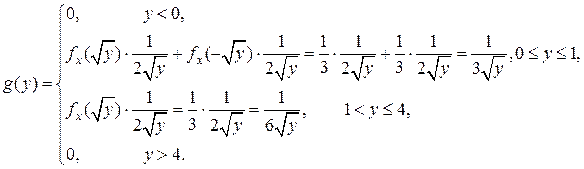Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 6. Непрерывная случайная величинаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Условия вариантов задачи В задачах 6.1-6.40 (параметры заданий приведены в табл. 6.1) случайная величина Х задана плотностью вероятности
Определить константу С, математическое ожидание, дисперсию, функцию распределения величины Х, а также вероятность ее попадания в интервал Таблица 6.1
Методические указания
Случайная величина Х называется непрерывной, если ее функция распределения F(x) – непрерывная и дифференцируемая функция для всех значений аргумента. Плотность распределения (или плотность вероятности) f (x) непрерывной случайной величины X в точке x характеризует плотность вероятности в окрестностях точки x и равна производной функции распределения этой СВ:
График плотности распределения называется кривой распределения. Вероятность попадания случайной величины X на произвольный участок
В геометрической интерпретации вероятность Соотношение (6.2) позволяет выразить функцию распределения F (x) случайной величины X через ее плотность:
Основные свойства плотности распределения: 1. Плотность распределения неотрицательна: f (x) 0. Причем f (x) = 0 для тех значений x, которые СВ никогда не принимает в опыте. 2. Условие нормировки:
Математическое ожидание характеризует среднее значение случайной величины и для непрерывной СВ определяется по формуле
Дисперсияслучайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания и для непрерывной СВ определяется по формуле
Дисперсия случайной величины имеет размерность квадрата случайной величины, поэтому для анализа диапазона значений величины Х дисперсия не совсем удобна. Этого недостатка лишено среднее квадратическое отклонение (СКО), размерность которого совпадает с размерностью случайной величины. Среднее квадратическое отклонение случайной величины X характеризует ширину диапазона значений X и равно
Правило
Примеры Пример 6.1. Случайная величина X распределена по закону, определяемому плотностью вероятности вида
Определить константу с, функцию распределения F(x), математическое ожидание, дисперсию величины Х, а также вероятность ее попадания в интервал Решение. Вначале вычислим значение константы с из условия нормировки (6.4). Условие нормировки представляет собой интегральное уравнение, из которого можно определить неизвестный параметр плотности вероятности. Для этого определим значение интеграла в левой части условия нормировки:
Из условия нормировки следует:
Плотность вероятности примет вид
Определим функцию распределения F(x). Так как плотность вероятности задана различными формулами на разных интервалах, то и ее первообразную - функцию распределения – будем искать по формуле (6.3) для каждого интервала в отдельности. Для для для Окончательно имеем
Вычислим вероятность
Так как правый край интервала Вычислим математическое ожидание СВ по формуле (6.5):
Дисперсиюслучайной величины СВ вычислим по формуле (6.6):
Пример 6.2. Определить по правилу Решение. Вычислим среднее квадратическое отклонение СВ по формуле (6.7):
Оценим диапазона значений X по формуле (6.8):
Как видим, получился интервал, полностью охватывающий точный диапазон значений СВ
Задача 7. Закон распределения функции случайного аргумента Условия вариантов задачи В задачах 7.1-7.40 (условия приведены в табл. 7.1) случайная величина Х распределена равномерно на интервале [ a,b ]. Построить график случайной величины Y=j(X) и определить плотность вероятности g(y). Таблица 7.1
Методические указания
Рассмотрим функцию одного случайного аргумента 1. Построить график 2. Диапазон Y разбить на M интервалов, в каждом из которых одинаковая степень неоднозначности ki, i =1,2, …, M:
Степень неоднозначности ki – число значений Х, соответствующих одному значению Y, или число обратных функций 3. Определить обратные функции 4. Определить плотность вероятностей
Примеры Пример 7.1. Определить плотность вероятности величины Решение. 1. Построим график величины
Рис. 7.1
2. В зависимости от числа k обратных функций выделим следующие интервалы для Y:
3. На интервалах В интервале
Вычислим модули производных обратных функций
В интервале
4. Так как Х равномерно распределена в интервале [-1, 2], то ее плотность вероятности равна
По формуле (7.1) получим плотность вероятности величины Y
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1997; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.008 с.) |


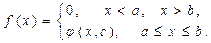
 .
.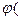 x,c)
x,c)
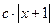
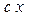
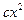
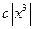

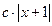
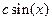
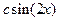
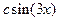
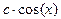
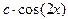
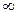
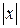
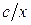
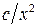
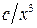
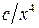
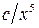
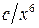
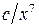
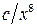
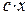
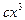
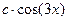
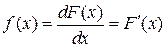 . (6.1)
. (6.1) равна сумме элементарных вероятностей на этом участке:
равна сумме элементарных вероятностей на этом участке: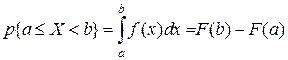 . (6.2)
. (6.2) равна площади, ограниченной сверху кривой распределения f (x) и отрезком
равна площади, ограниченной сверху кривой распределения f (x) и отрезком 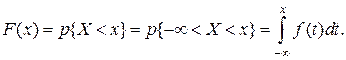 (6.3)
(6.3)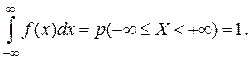 (6.4)
(6.4)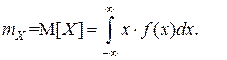 (6.5)
(6.5)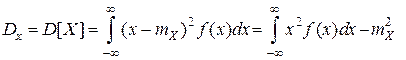 . (6.6)
. (6.6)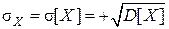 . (6.7)
. (6.7)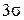 . Практически все значения случайной величины находятся в интервале
. Практически все значения случайной величины находятся в интервале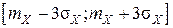 . (6.8)
. (6.8)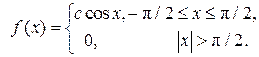
 .
.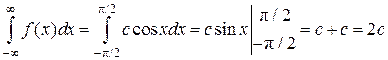 .
.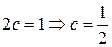 .
.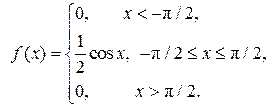
 :
: 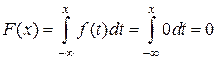 ,
,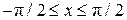 :
: 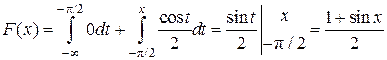 ,
,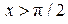 :
: 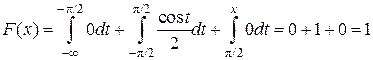 .
.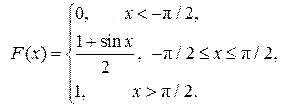
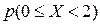 по формуле (6.2):
по формуле (6.2):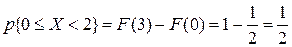 .
.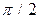 , то
, то 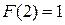 .
.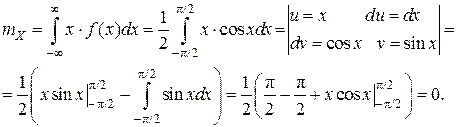
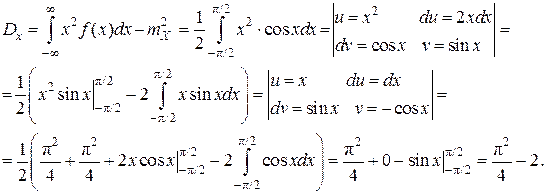
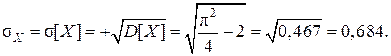
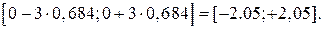
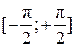 , который можно определить по свойству 1 плотности вероятности.
, который можно определить по свойству 1 плотности вероятности.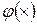
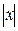
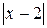
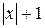
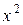
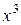
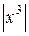
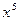
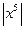
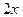
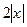
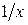
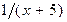
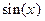
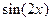
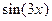
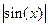
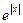
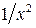
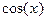
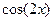
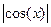
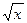
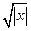
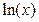
 . Если X – непрерывная случайная величина с известной плотность вероятности
. Если X – непрерывная случайная величина с известной плотность вероятности 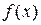 , то алгоритм получения плотность вероятности g (y) величины Y следующий:
, то алгоритм получения плотность вероятности g (y) величины Y следующий: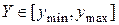 .
.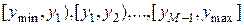 .
.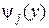 для данного интервала, j = 1,2, …, ki.
для данного интервала, j = 1,2, …, ki.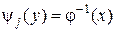 и вычислить модули производных обратных функций
и вычислить модули производных обратных функций 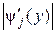 . В общем случае число обратных функций
. В общем случае число обратных функций 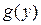 по следующей формуле:
по следующей формуле: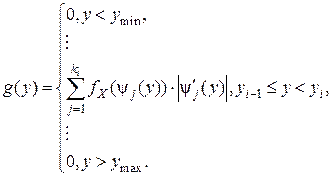 (7.1)
(7.1)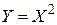 , если X - случайная величина, равномерно распределенная на интервале
, если X - случайная величина, равномерно распределенная на интервале 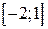 .
.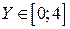 (рис. 7.1).
(рис. 7.1).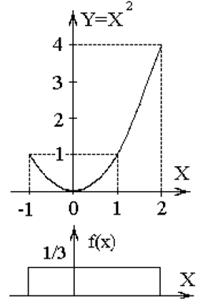
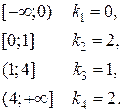
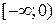 и
и 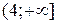 обратные функции не существует.
обратные функции не существует.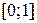 две обратных функции:
две обратных функции: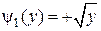 и
и 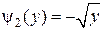 .
.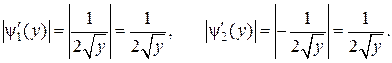
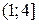 одна обратная функция
одна обратная функция 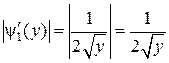 .
.