
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка регрессионных характеристик ⇐ ПредыдущаяСтр 9 из 9
Регрессией случайной величины Y на x называется условное математическое ожидание Необходимо на основании имеющейся выборки выявить характер связи между величинами X, Y, т.е. получить оценку условного математического ожидания
где Для определения типа зависимости строится диаграмма рассеивания или корреляционное поле, которую можно получить, если результаты опытов изобразить в виде точек на плоскости в декартовой системе координат. На основании анализа корреляционного поля выбираем тип линии регрессии Если величины X и Y распределены по нормальному закону, то регрессия является линейной:
Оценки параметров для линейной регрессии
где
Для визуальной проверки правильности вычисления величин Примеры Пример 11.1. По выборке двухмерной случайной величины, которая содержит 50 пар значений (x,y) (первые два столбца таб. 11.1): – вычислить точечную оценку коэффициента корреляции; – вычислить интервальную оценку коэффициента корреляции (γ= 0,95); – проверить гипотезу об отсутствии корреляционной зависимости (a = 0,05); – вычислить оценки параметров – построить диаграмму рассеивания и линию регрессии. Решение. Для решения задачи удобно воспользоваться приведенной ниже таблицей. Значения в 3-ем, 4-ом и 5-ом столбцах вычисляются по формулам, приведенными в первой строке таблицы. В последней строке таблицы приведены средние арифметические значений каждого из столбцов. Таким образом получены:
- оценки математических ожиданий по каждой переменной (см. (11.1)):
- оценки начальных моментов второго порядка по каждой переменной:
- оценка смешанного начального момента второго порядка:
Таблица 11.1
На основе этих данных легко вычислить оценки дисперсий (см. (11.2)):
и оценку корреляционного момента (см. (11.3))
Вычислим точечную оценку коэффициент корреляции по формуле (11.4):
Вычислим интервальную оценку коэффициента корреляции с надежностью γ = 0,95 по формуле (11.5). Для этого в таблице функции Лапласа (см. Приложение 2) найдем значение, равное
Таким образом, доверительный интервал для коэффициента корреляции имеет вид
Проверим гипотезу об отсутствии корреляционной зависимости:
Так как объем выборки велик (n ≥ 50), то вычислим значение критерия по формуле (11.7):
Определим значение Zα из таблицы функции Лапласа (см. Приложение 2):
Так как Вычислим оценки параметров
Уравнение линии регрессии имеет вид:
Построим диаграмму рассеивания, изобразив значения исходной двумерной выборки
Рис. 11.1 Диаграмма рассеивания и линия регрессии
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 91; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.182.179 (0.017 с.) |
 случайной величины Y при условии, что X = x. Регрессия Y на x устанавливает зависимость среднего значения величины Y от величины X. Если случайные величины X и Y независимы, то
случайной величины Y при условии, что X = x. Регрессия Y на x устанавливает зависимость среднего значения величины Y от величины X. Если случайные величины X и Y независимы, то 
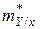 - оценку регрессии Y на х. Данная оценка представляет собой некоторую функцию:
- оценку регрессии Y на х. Данная оценка представляет собой некоторую функцию: ,
, – неизвестные параметры.
– неизвестные параметры. . Значения параметров
. Значения параметров 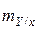 , т.е. ее значения должны быть приблизительно равны средним арифметическим значений Y для каждого значения Х = х.
, т.е. ее значения должны быть приблизительно равны средним арифметическим значений Y для каждого значения Х = х.
 определяются по формулам
определяются по формулам (11.8)
(11.8) – оценки математического ожидания величин X и Y;
– оценки математического ожидания величин X и Y; – оценка дисперсии величины X;
– оценка дисперсии величины X; – оценка корреляционного момента величин X и Y.
– оценка корреляционного момента величин X и Y. необходимо построить диаграмму рассеивания и график
необходимо построить диаграмму рассеивания и график  рассчитаны без грубых ошибок, то сумма квадратов отклонений всех значений (точек) двухмерной выборки
рассчитаны без грубых ошибок, то сумма квадратов отклонений всех значений (точек) двухмерной выборки 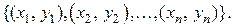 от прямой
от прямой  и
и  линии регрессии
линии регрессии 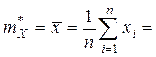 5,08 (см. столбец 2),
5,08 (см. столбец 2), 5,21 (см. столбец 3);
5,21 (см. столбец 3);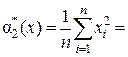 34,55755 (см. столбец 4),
34,55755 (см. столбец 4), 36,09954 (см. столбец 5);
36,09954 (см. столбец 5);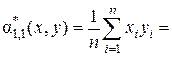 27,98996 (см. столбец 6).
27,98996 (см. столбец 6). 8,74746;
8,74746; 8,86278
8,86278 1,476106
1,476106 0,168.
0,168. и определим значение аргумента, ему соответствующее:
и определим значение аргумента, ему соответствующее:  (строка 1,9, столбец 6). Вычислим вспомогательные значения a, b:
(строка 1,9, столбец 6). Вычислим вспомогательные значения a, b:

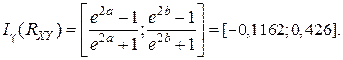

 .
.
 , то гипотеза H 0 принимается, т.е. величины X и Y некоррелированны.
, то гипотеза H 0 принимается, т.е. величины X и Y некоррелированны.

 в виде точек с координатами
в виде точек с координатами  на плоскости в декартовой системе координат, и линию регрессии (рис. 11.1).
на плоскости в декартовой системе координат, и линию регрессии (рис. 11.1).



