
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные комбинаторные формулыСодержание книги
Поиск на нашем сайте
При решении задач по классическому определению вероятности используются следующие комбинаторные формулы. Размещения: – без повторений элементов
– c повторением элементов
Формулы для размещений позволяет подсчитать количество комбинаций из n элементов по m, где комбинации будут отличаться как самими элементами, так и расположением их относительно друг друга. Сочетания: – без повторений элементов
– с повторением элементов
Формулы для сочетаний позволяет подсчитать количество комбинаций из n элементов по m, где комбинации будут отличаться только самими элементами, т.е. каждая комбинация хотя бы одним элементом должна отличаться от другой. Перестановки:
Формула для перестановок позволяет подсчитать количество комбинаций из n элементов, где комбинации будут отличаться только расположением их относительно друг друга. Примеры Пример 1.1. Какова вероятность того, что наудачу взятый телефонный номер из 7 цифр имеет все цифры различные. Решение. Определим событие А. Событие А состоит в том, что в семизначном номере все цифры различны. Так как номер семизначный, а цифр всего 10, то общее число исходов n опыта равно числу размещений c повторением элементов из 10 по 7:
Пример 1.2. Наудачу взяты два положительных числа x и y, причем Решение. Подставляя значения коэффициентов в неравенства, получаем:
Строим на рис. 1.2 оси координат и область, которая определяет пространство элементарных событий Ω. Она задается неравенствами
Рис. 1.2. Площадь прямоугольника
Задача 2. Теоремы сложения и умножения вероятностей
Условия вариантов задачи Ниже приведены 40 вариантов задачи 2. Номер варианта задачи, которую студент должен решить, указан в индивидуальном задании.
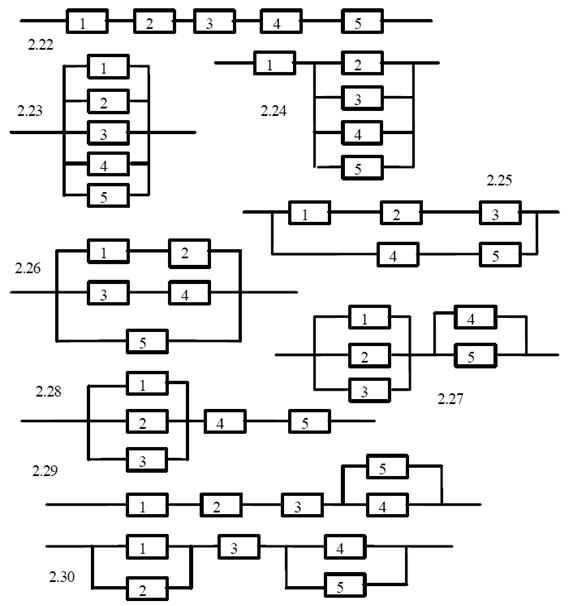
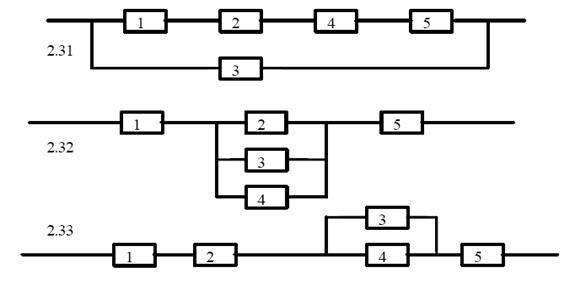
В задачах 2.1-2.40 приведены схемы соединения элементов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5 соответственно равны q1=0,1; q2=0,2; q3=0,3; q4=0,4; q5=0,5 q6=0,6. Найти вероятность того, что сигнал пройдет со входа на выход.
Вероятность суммы (объединения) двух произвольных случайных событий (т.е. тех, которые могут происходить совместно) равна сумме вероятностей каждого из событий минус вероятность их совместного появления:
Для трех произвольных событий:
Для n произвольных событий:
Событие A называется независимым от события B, если возможность наступления события A не зависит от того, произошло событие B или нет. В противном случае события являются зависимыми. Условной вероятностью Вероятность произведения (пересечения) двух случайных событий равна вероятности одного из них, умноженной на условную вероятность второго при наличии первого.
Для независимых событий
Вероятность произведения n произвольных событий
где
В случае независимых событий данная формула упрощается:
Примеры Пример 2.1. Вычислительная машина (ВМ) состоит из n блоков. Вероятность безотказной работы в течении времени Т (надежность) первого блока равна p 1, второго – p 2, и т.д. Блоки отказывают независимо друг от друга. При отказе любого блока отказывает ВМ. Найти вероятность того, что ВМ откажет за время Т. Решение. Рассмотрим события А 1 – отказывает 1-й блок, А 2 – отказывает 2-й блок и т.д.. Пусть событие В – отказ вычислительной машины. Это событие произойдет тогда, когда выполнится или событие А 1, или событие А 2 и т.д.. Видим, что следует применять теорему о сумме или объединении n произвольных событий, формула (2.3):
События Ai являются независимыми, поэтому правая часть запишется в виде:
Вероятности противоположных событий
Пример 2.2. Дана схема электрической цепи (рис. 2.1).
Рис. 2.1 Вероятности работы элементов цепи 1, 2, 3 соответственно равны друга. Найти вероятность того, что ток пройдет из точки 1 в точку 2. Решение. Опишем через события работу элементов цепи. Пусть событие А 1 состоит в том, что работает элемент 1, событие А 2 – элемент 2, событие А 3 –элемент 3. Тогда вероятности этих событий запишутся так:
Анализируем заданную цепь и определяем участки цепи с последовательным и параллельным соединением. На рис. 2.1 элементы 2, 3 соединены параллельно. А элемент 1 соединен последовательно с элементами 2, 3. Поэтому введем событие А состоящее в том, что ток пройдет из точки 1 в точку 3, оно выполнится тогда, когда будет работать элемент 1. Можно записать: А=А 1. Введем событие В, состоящее в том, что ток пройдет из точки 2 в точку 3; оно произойдет тогда, когда будут работать или элемент 2, или элемент 3. Тогда событие В можно описать так:
Найдем вероятности событий, входящих в правую часть формулы (2.8):
Подставляя полученные значения в формулу (2.8), получим
|
||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.9.138 (0.01 с.) |

 (1.6)
(1.6) (1.7)
(1.7) . (1.8)
. (1.8)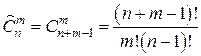 (1.9)
(1.9) (1.10)
(1.10) . Для подсчета благоприятствующих исходов подходит формула для размещений без повторения элементов:
. Для подсчета благоприятствующих исходов подходит формула для размещений без повторения элементов:  . Тогда
. Тогда .
. . Найти вероятность того, что
. Найти вероятность того, что  и
и  , если
, если  .
. (1.11)
(1.11)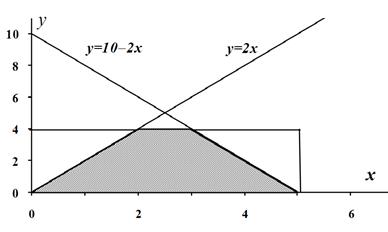
 . Область благоприятствующих исходов определяется неравенствами (1.11), поэтому строим на рисунке прямые, которые задаются неравенствами (1.11). Заштрихованная на рисунке 1.2 область и описывает благоприятствующие исходы (с учетом всех возможных значений), площадь этой заштрихованной трапеции равна
. Область благоприятствующих исходов определяется неравенствами (1.11), поэтому строим на рисунке прямые, которые задаются неравенствами (1.11). Заштрихованная на рисунке 1.2 область и описывает благоприятствующие исходы (с учетом всех возможных значений), площадь этой заштрихованной трапеции равна  [у. е.]. Тогда вероятность события А равна
[у. е.]. Тогда вероятность события А равна .
.



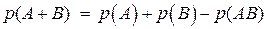 . (2.1)
. (2.1) (2.2)
(2.2) . (2.3)
. (2.3) называется вероятность события В, вычисленная при условии (в предположении), что событие А произошло. Для независимых событий
называется вероятность события В, вычисленная при условии (в предположении), что событие А произошло. Для независимых событий  .
. . (2.4)
. (2.4) . (2.5)
. (2.5)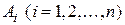 равна
равна (2.6)
(2.6) ) – условная вероятность появления события
) – условная вероятность появления события  , при условии, что события
, при условии, что события  в данном опыте произошли,
в данном опыте произошли, 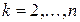 .
. . (2.7)
. (2.7) .
. .
. (здесь событие
(здесь событие  Окончательно получаем
Окончательно получаем .
.
 . Элементы цепи отказывают независимо друг от
. Элементы цепи отказывают независимо друг от . Найдем вероятности противоположных событий (т.е. того, что элементы 1, 2, 3 не работают и ток через них не идет), используя (1.3):
. Найдем вероятности противоположных событий (т.е. того, что элементы 1, 2, 3 не работают и ток через них не идет), используя (1.3): .
. . Рассмотрим событие С состоящее в том, что ток пройдет из точки 1 в точку 2, оно выполнится тогда, когда выполнится и событие А и событие В. Событие С запишется так:
. Рассмотрим событие С состоящее в том, что ток пройдет из точки 1 в точку 2, оно выполнится тогда, когда выполнится и событие А и событие В. Событие С запишется так:  . По условию задачи необходимо найти вероятность события С (учтем, что события А и В независимы), используем (2.5):
. По условию задачи необходимо найти вероятность события С (учтем, что события А и В независимы), используем (2.5): (2.8)
(2.8) , а
, а  см. формулу (2.3)
см. формулу (2.3) 





