
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 5. Дискретная случайная величинаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Условия вариантов задачи В задачах 5.1-5.40 дискретная случайная величина Х может принимать одно из пяти фиксированных значений x1, x2, x3, x4, x5 с вероятностями p1, p2, p3, p4, p5 соответственно (конкретные значения приведены в таб. 5.1). Найти p отмеченные *. Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения. Таблица. 5.1
Методические указания
Случайная величина (СВ) – это величина, которая в результате опыта со случайным исходом принимает то или иное значение, причем заранее до опыта неизвестно, какое именно. Обозначения случайной величины: X, Y; а их значения: x, y. Случайная величина Х называется дискретной, если ее множество возможных значений W X – счетное, т.е. элементы множества можно расположить в определенном порядке и пронумеровать. Закон распределения случайной величины — любое правило, устанавливающее соответствие между значениями случайной величины и вероятностями ее наступления. Рядом распределения дискретной СВ X называется таблица, в верхней строке которой перечислены все возможные значения СВ
Так как события
Функцией распределения случайной величины X называется вероятность того, что она примет значение меньшее, чем аргумент x функции F(x): Свойства функции распределения: 1. F (-) = 0 и F (+) = 1. 2. Неубывающая функция: 4. Вероятность попадания значения СВ X в интервал
Функция распределения дискретной СВ определяется так:
где Здесь суммируются вероятности всех тех значений
Функция распределения любой дискретной СВ есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятностям этих значений. Математическое ожидание характеризует среднее значение случайной величины и для дискретной СВ определяется по формуле
Как видно из (5.4), в качестве математического ожидания СВ используется «среднее взвешенное значение», причем каждое из значений случайной величины учитывается с «весом», пропорциональным вероятности этого значения. Дисперсияслучайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания и для дискретной СВ определяется по формуле:
Примеры Пример 5.1. По командному пункту противника производится пуск трех ракет, причем вероятность попадания в цель при пуске одной ракеты равна 0,8. Построить ряд распределения числа попаданий. Решение. Определим случайную величину X как число попаданий в цель при трех пусках ракет. Эта случайная величина может принимать следующие значения: 0, 1, 2, 3. Найдем вероятность принятия величиной X этих значений, используя формулу Бернулли:
Ряд распределения имеет следующий вид
Как видим, условие (5.1) выполняется. Пример 5.2. Зная ряд распределения для случайной величина X, описанной в примере 5.1, построить график функции распределения. Найти математическое ожидание и дисперсию дискретной случайной величины X. Решение. Рассчитаем значения функции распределения для фиксированных значений 1. 2. 3. 4. 5. При
Рис. 5.1 Опишем построение графика функции распределения F(x) (рис. 5.1). Рассмотрим первый промежуток по оси Х от Математическое ожидание дискретной СВ X определим по формуле (5.4):
Дисперсию дискретной СВ X определим по формуле (5.5):
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1055; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.60.132 (0.007 с.) |

 , а в нижней — вероятности их появления
, а в нижней — вероятности их появления  , где
, где  :
:



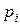



 несовместны и образуют полную группу, то справедливо контрольное соотношение
несовместны и образуют полную группу, то справедливо контрольное соотношение . (5.1)
. (5.1) .
.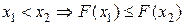 .
. :
: (5.2)
(5.2) (5.3)
(5.3) – вероятности ряд распределения этой СВ.
– вероятности ряд распределения этой СВ.






 (5.4)
(5.4) (5.5)
(5.5)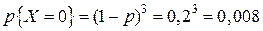 ,
,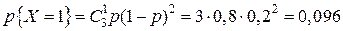 ,
, ,
, .
. , взятых из ряда распределения (пример 5.1).
, взятых из ряда распределения (пример 5.1). .
.
 .
.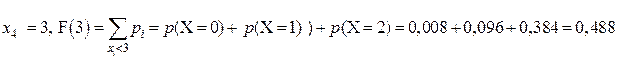
 , согласно свойствам функции распределения,
, согласно свойствам функции распределения, 

 до 0; согласно пункту 1 значение
до 0; согласно пункту 1 значение  и линия идет по оси Х до нуля включительно. Второй промежуток по оси Х от 0 до 1; согласно пункту 2 значение
и линия идет по оси Х до нуля включительно. Второй промежуток по оси Х от 0 до 1; согласно пункту 2 значение  значит проводим ступеньку высотой 0,008. Третий промежуток от 1 до 2; согласно пункту 3 значение
значит проводим ступеньку высотой 0,008. Третий промежуток от 1 до 2; согласно пункту 3 значение  значит проводим ступеньку высотой 0,104. Четвертый промежуток от 2 до 3; согласно пункту 4 значение
значит проводим ступеньку высотой 0,104. Четвертый промежуток от 2 до 3; согласно пункту 4 значение 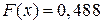 значит проводим ступеньку высотой 0,488. Пятый промежуток от 3 до
значит проводим ступеньку высотой 0,488. Пятый промежуток от 3 до  ; согласно пункту 5 значение
; согласно пункту 5 значение  значит проводим ступеньку высотой 1.
значит проводим ступеньку высотой 1. ,
,



