
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 8. Двухмерные случайные величины
Условия вариантов задачи
В задачах 8.1-8.40 (конкретные параметры приведены в табл. 8.1) двухмерный случайный вектор (Х, У) равномерно распределен внутри выделенной жирными прямыми линиями на рис. 8.1 области B. Двухмерная плотность вероятности f(x,y) одинакова для любой точки этой области B:
Вычислить коэффициент корреляции между величинами X и Y.
Рис. 8.1
Методические указания
Двухмерная случайная величина (Х,Y) – совокупность двух одномерных случайных величин, которые принимают значения в результате проведения одного и того же опыта. Двухмерную случайную величину (Х,Y) геометрически можно представить как случайную точку (Х,У) на плоскости хOу.
Двухмерная случайная величина (X,Y) является непрерывной, если ее функция распределения F(х,у) представляет собой непрерывную, дифференцируемою функцию по каждому из аргументов и существует вторая смешанная производная Двухмерная плотность распределения f(х,у) характеризует плотность вероятности в окрестности точки с координатами (х,у) и равна второй смешанной производной функция распределения:
Свойства двухмерной плотности: 1. 2. 3. 4. Условие нормировки: Геометрически интеграл условия нормировки вычисляет объем тела, ограниченный поверхностью распределения и плоскостью хOу. 5.
Математические ожидания компонент двухмерной непрерывной случайной величины (X,Y) вычисляются по формулам
Дисперсии компонент двухмерной непрерывной случайной величины (X,Y) вычисляются по формулам
Корреляционный момент
Коэффициент корреляции
Для любых случайных величин Примеры Пример 8.1. Двухмерный случайный вектор (X, Y) равномерно распределен внутри области B, выделенной жирными прямыми линиями на рис. 8.1. Двухмерная плотность вероятности f(x,y) одинакова для любой точки этой области B:
Вычислить коэффициент корреляции между величинами X и Y, если координаты вершин области B приведены в таб. 8.2. Таблица 8.2
Решение. Построим область B. Соединим последовательно точки с координатами из таб. 8.2 согласно рис. 8.1: – точку (x1;0) = (0;0) c точкой (x2; y2) = (1; 1), – точку (x2; y2) = (1; 1) c точкой (x3; y2) = (1; 1) (т.е. остаемся на месте), – точку (x3; y2) = (1; 1) c точкой (x4; y1) = (2; 0,5), – точку (x4; y1) = (2; 0,5) c точкой (x5; y1) = (2; 0,5) (т.е. остаемся на месте), – точку (x5; y1) = (2; 0,5) c точкой (x6; 0) = (3; 0). В результате получим следующую фигуру (рис. 8.2):
Рис. 8.2 Совместная плотность вероятности примет вид
Неизвестную константу c определим, используя условие нормировки плотности вероятности (см. (8.4)):
Таким образом
Проверим геометрически полученный результат. Объем тела, ограниченный поверхностью распределения и плоскостью xOy должен быть равен единице, т.е. объем прямой треугольной призмы равен Вычислим математические ожидания по формулам (8.6) и (8.7):
Вычислим дисперсии по формулам (8.8) и (8.9)
Корреляционный моментвычислим по формуле (8.10):
После нормировки по формуле (8.11) получаем коэффициент корреляции
Задача 9. Числовые характеристики суммы и произведения случайных величин
Условия вариантов задачи
В задачах 9.1-9.40 вычислить математическое ожидание и дисперсию величин U и V, а так же определить их коэффициент корреляции
Конкретные значения коэффициентов Таблица 9.1
Методические указания
Числовые характеристики суммы Пусть – математическое ожидание Y равно
где – дисперсия Y равно:
где
Если
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1459; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.171.12 (0.042 с.) |



 Таблица 1.4
Таблица 1.4 .
. . (8.1)
. (8.1) .
. . (8.2)
. (8.2) . (8.3)
. (8.3) . (8.4)
. (8.4) ;
;  . (8.5)
. (8.5) (8.6)
(8.6) (8.7)
(8.7) (8.8)
(8.8)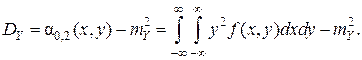 (8.9)
(8.9)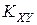 характеризует степень тесноты линейной зависимости величин X и Y, а также рассеивание их значений относительно точки (mX, mY):
характеризует степень тесноты линейной зависимости величин X и Y, а также рассеивание их значений относительно точки (mX, mY): . (8.10)
. (8.10) характеризует только степень линейной зависимости величин и равен нормированному корреляционному моменту:
характеризует только степень линейной зависимости величин и равен нормированному корреляционному моменту: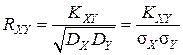 . (8.11)
. (8.11) |. Если величины X и Y независимы, то
|. Если величины X и Y независимы, то  .
.




 .
.

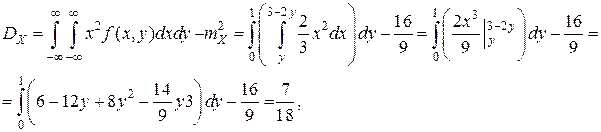

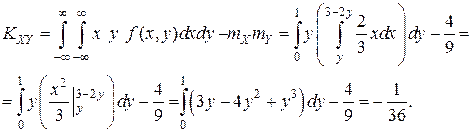
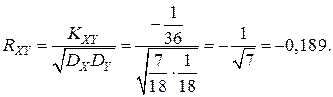
 :
: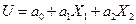
 .
. и числовые характеристики случайных величин
и числовые характеристики случайных величин  приведены в табл. 9.1.
приведены в табл. 9.1.
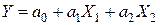 , где
, где  – не случайные коэффициенты, тогда
– не случайные коэффициенты, тогда , (9.1)
, (9.1) – математическое ожидание СВ Xi;
– математическое ожидание СВ Xi;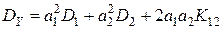 , (9.2)
, (9.2) – дисперсия СВ Xi ,
– дисперсия СВ Xi , – корреляционный момент величин X1 и X2.
– корреляционный момент величин X1 и X2. ,
,  ; (9.3)
; (9.3) . (9.4)
. (9.4)


