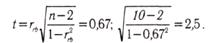Вычисление коэффициента ассоциации Пирсона при сравнении параллельных форм опросника

Примечание: 0 — несовпадение с «клю­чом»; 1 — совпадение с «ключом».

 

В случае, если данные представлены в виде частот совпадений событий в четы­рех возможных вариантах сочетания пе­ременных (табл. 8), коэффициент φ будет иметь вид:

 

Коэффициент φ удобен при расчете надежности ретестовой, а также анали­за устойчивости ответов на пункты (зада­ния) и степени их трудности, что особенно ценно при конструировании тестов. Применяя коэффициент φ и определив со­ответствие данных в сравниваемых сери­ях (тест—ретест), можно одновременно оценить степень оптимальности задания по силе (трудности) (см. Трудность заданий теста). Значение φ обратно про­порционально отношению частоты пра­вильных и неправильных ответов! Погра­ничные варианты (задачи, решаемые все­ми, и задачи чрезмерно сложные, решае­мые относительно небольшим числом об­следованных) обычно исключаются из те­ста как неинформативные и неустойчи­вые. Пороговой величиной неустойчи­вости пункта теста является превышение значения

 

Таблица 8

Вычисление четырехпольного коэффициента ассоциации Пирсона (ф)*

 

При анализе опросников личностных с дихотомической формой ответов («да»— «нет», «верно»—«неверно» и т. д.) состав­ляемая в ходе расчета коэффициента φ четырехклеточная матрица позволяет установить несимметричное распределе­ние утвердительных и отрицательных от­ветов.

При анализе четырехклеточных ассо­циаций используется также коэффициент Юла:

Этот коэффициент, в отличие от φ, вы­ражает одностороннюю связь, т. е. влия­ние одного признака на другой (в при­мере из табл. 7 — влияние тестового ре­зультата на вывод об уровне развития). Значение Q варьирует от -1 до +1. При Q = 0 признаки независимы, Q = 1 свиде­тельствует о положительной зависимости (всем Х= 1 соответствует У= 1); При Q = -1 — связь отрицательная. В силу того что Q выражает одностороннюю связь, его значения обычно превышают значения φ (в примере φ = 0,36; Q - 0,67). В настоящем разделе рассмот­рены случаи определения корреляции двух дихотомических переменных. Когда одна из переменных дихотомическая, а другая выражена в шкале интервалов или отношений (см. Шкалы измеритель­ные), используются коэффициенты кор­реляции бисериальные (см. Корреляция бисериальная).

КОРРЕЛЯЦИОННЫЙ АНАЛИЗ -комплекс методов статистического иссле­дования взаимозависимости между пере­менными, связанными корреляционными отношениями. Корреляционными (лат. correlatio — соотношение, связь, зависи­мость) считаются такие отношения меж­ду переменными, при которых выступает преимущественно нелинейная их зависи­мость, т. е. значению любой произвольно взятой переменной одного ряда может со­ответствовать некоторое количество зна­чений переменной другого ряда, откло­няющихся в ту или иную сторону от среднего.

К. а. выступает в качестве одного из вспомогательных методов решения теоре­тических задач психодиагностики и вклю­чает в себя комплекс наиболее широко применяемых статистических процедур при разработке тестовых и других психо­диагностических методик, определения их надежности, валидности. К. а. явля­ется одним из основных методов статис­тической обработки эмпирического мате­риала в прикладных психодиагностичес­ких исследованиях.

Существующие процедуры К. а. поз­воляют определить степень значимости связи, установить меру и направление влияния одного из признаков (X) на ре­зультирующий признак (Y) при фиксиро­ванном значении отдельных переменных (корреляция частная), выявить степень и направленность связи результирующего признака (Y) с совокупностью перемен­ных x₁, x₂,..., x_k (корреляция множе­ственная). К. а. подлежат как количе­ственные, так и качественные признаки (к первым относятся переменные, измеряе­мые в интервальной шкале и шкале отношений, ко вторым — не имеющие единиц измерения, оцениваемые шкалами наиме­нований и порядковыми шкалами) (см. Шкалы измерительные). Может быть также установлена корреляция и для при­знаков, один из которых является каче­ственным, а другие количественными (корреляция бисериальная, корреляция качественных признаков).

Одним из основных принципов опреде­ления количественных критериев корре­ляционной связи — коэффициентов кор­реляции — является сравнение величин отклонений от среднего значения по каж­дой группе в сопряженных парах сравни­ваемых рядов переменных. Другими сло­вами, определяется частота соответствия между шкалами X и Y. Предположим, один и тот же испытуемый получил высо­кие оценки по тесту вербальных способ­ностей (Х₁) и показателям успеваемости по литературе (Y₁). Тогда произведения отклонений и принимают высо­кие положительные значения. Если же большому х,₁ у другого испытуемого будет соответствовать малое y ₁ то это произве­дение будет отрицательным. Абсолютная величина произведения отклонений зави­сит от степени отклонения переменных от среднего значения в сравниваемых парах. Если X и У не имеют систематической связи (большие х сочетаются с малыми у и наоборот), различные произведения будут принимать положительные или отрицательные значения. Сумма произ­ведений во всех сравниваемых парах

 

будет приближаться к нулю. Сумма про­изведений в сравниваемых рядах переменных будет иметь большую величину по модулю и положительный знак, если X и У связаны между собой выраженной прямой зависимостью, и большую величи­ну и отрицательный знак при связи X и У сильной обратной зависимости.

С целью достижения независимости меры корреляционной связи от числа сравниваемых пар и величин стандартных отклонений в двух группах произведение отклонений делится на число сравниваемых пар и стандартные отклонения в сопоставимых рядах. Такая мера носит на­звание коэффициента корреляции — про­изведения моментов Пирсона:

 

где x_t и y₁, — сравниваемые количествен­ные признаки, п — число сравниваемых наблюдений, σ_х и σ_у — стандартные от­клонения в сопоставимых рядах. Расчет­ная формула r_ху имеет следующий вид:

 

При вычислении коэффициента Пир­сона, особенно при большом количестве наблюдений, целесообразно упрощение за счет различных приемов, сокращаю­щих объем вычислений. В качестве при­мера приводим расчет результатов двух тестов в группе из 10 обследованных (табл. 9).

 

Таблица9

Вычисление коэффициента корреляции произведения моментов Пирсона (r_ху)

 

 

Определение статистической зависи­мости коэффициента r_ху проводится с по­мощью критерия Стьюдента (t):

 

где п' — число степеней свободы (n ' = п - 2). По таблице распределения Стью­дента для п' = 8 находим t = 2,896 при α = 0,02 и t = 2,306 при α = 0,05. Отсюда статистическая значимость установленного значения корреляции признаков на уровне α > 0,02.

При возведении коэффициента корре­ляции Пирсона в квадрат получаем коэф­фициент детерминации r²_ху, выражаю­щий степень вариации переменных. В на­шем примере r²_ху = 0,48, что свидетель­ствует о том, что 48% измерений призна­ков объясняются их совместным распре­делением (взаимовлиянием).

КОРРЕЛЯЦИЯ БИСЕРИАЛЬНАЯ (лат. bis series — два ряда, две серии) — метод корреляционного анализа отноше­ния переменных, одна из которых измере­на в дихотомической шкале наименова­ний, а другая — в интервальной шкале отношений или порядковой шкале. Назва­ние метода связано с тем, что сравнивают­ся две альтернативные серии объектов X, имеющие условные значения 0 или 1 по У.

Наиболее характерно применение ко­эффициентов К. б. в психологической диагностике при анализе дискриминативности заданий теста, а также при определении валидности критериаль­ной путем коррелирования значений тес­товых оценок с независимыми характе­ристиками критерия, выраженными в ди­хотомической шкале (см. Шкалы изме­рительные).

Для описания связи между перечис­ленными видами переменных исполь­зуется точечный бисериальный коэффи­циент корреляции Пирсона:

 

где — среднее по X объектов со значе­нием единицы по У; — среднее по X объектов со значением нуль по Y; S_x — стандартное отклонение всех значений по X; n₁ — число объектов, с единицей по Y: n₀ — число объектов с нулем по Y, т. е. п = п₁ + n₀. Уравнение для вычисления r_pb представляет собой алгебраическое упрощение формулы коэффициента r_ху (см. Корреляционный анализ) для слу­чая, когда Y — дихотомическая перемен­ная. Можно привести ряд других эквива­лентных выражений, удобных для прак­тического применения:

 

где х — общее среднее по X.

Значение r_pb варьирует от -1 до +1. В том случае, когда переменные с единицей по У имеют среднее по X, равное средне­му переменных с нулем по У, r _рb обраща­ется в нуль.

В качестве примера можно привести вычисление r_pь при анализе дискриминативности отдельных пунктов опросника личностного, т. е. корреляции между ти­пичным ответом на отдельный пункт (утверждение—отрицание) с общим резуль­татом по тесту (табл. 10).

Вычисленное таким образом значение r_pb показывает, что проверяемый пункт опросника имеет среднюю диагностичес­кую значимость и слабо коррелирует с об­щим результатом теста.

Достоверность (α) связи, рассчитан­ной с помощью коэффициента r_pb, может определяться с помощью критерия χ² для числа степеней свободы df = 2.

Другим распространенным методом расчета является определение бисериального коэффициента корреляции (r_bis), ко­торый применяется в тех случаях, когда есть основания полагать, что дихотомическое распределение близко к нормаль­ному:

 

Элементы уравнения идентичны ис­пользуемым при вычислении r_pb, за исключением величины U — ординаты нормированного нормального распре­деления в точке, за которой лежит площади под кривой (см. Нормальное распределение). Из данных табл. 9 = = 0,61; ордината нормированного (единичного) нормального рас­пределения (U), за которой лежит 61% площади под кривой, равна 0,3836.

 

Таблица 10

Вычисление точечного бисериального ко­эффициента корреляции Пирсона

Примечание: 1 — совпадение с «клю­чом»; 0 — несовпадение с «ключом».

 

В отличие от других коэффициентов корреляции, r_bis может принимать значе­ния ниже -1 и выше +1. В случае попада­ния значения в эти области делается вы­вод о некорректности предположения о нормальном законе распределения X или о распределении значений X в выборке с эксцессом значительно ниже нормаль­ного. Следует обратить внимание на то обстоятельство, что при распределении переменных X с эксцессом больше нор­мального границы r_bis будут соответствен­но меньше пределов -1 и +1, что приве­дет к переоценке степени связи. Это требует тщательной проверки свойств распределения при использовании бисе­риального коэффициента корреляции.

При вычислении r_pb и r_bis оперируют одинаковыми исходными данными, однако эти коэффициенты не тождественны. Ко­эффициент r_pb более строг при характери­стике степени связи между X и Y (r_bis > r_pb). Случаи, когда одна из перемен­ных представлена в дихотомической шка­ле, а другая — в порядковой, требуют применения коэффициента рангово-бисериальной корреляции

 

где — средний ранг объектов, имею­щих 1 по X; — средний ранг объектов с 0 по X. Пример вычислений приведен в табл. 11. Коэффициент r_rb тесно связан с коэффициентом τ Кендалла. Особенно четко эта связь прослеживается при анализе корреляционной связи с помощью близкого к r_rb коэффициента r_pb в случае использования для его определения поня­тия совпадения и инверсии (см. Корреля­ция ранговая):

 

где n₀ — число объектов с нулевой дихотомией; п₁ — число объектов с еди­ничной дихотомией; Р — сумма совпаде­ний; Q — сумма инверсий.

 

Таблица 11

Вычисление рангово-бисериальной корреляции r_rb при сопоставлении результатов теста у девочек(1) и мальчиков(О)

При оценке значимости связи можно использовать критерий Стьюдента:

 

При количестве степеней свободы п' = п - 2 = 8t_кp = 2,306, при α = 0,05; t > t_кp, следовательно, при α < 0,05 выявленная связь является статистичес­ки значимой.

 

КОРРЕЛЯЦИЯ КАЧЕСТВЕННЫХ ПРИЗНАКОВ — метод анализа связи переменных, измеряемых в порядковых шкалах и шкалах наименований (см. Шкалы измерительные). Наиболее часто такой корреляционный анализ прово­дят с помощью коэффициентов корреля­ции ранговой, используемых в случаях, когда обе переменные измеряются в шка­лах порядка или легко могут быть преоб­разованы в ранги. При измерении сравни­ваемых переменных в шкалах наименова­ний широко применяются коэффициенты сопряженности, в которых в качестве про­межуточной расчетной величины исполь­зуется критерий согласия Пирсона (см. Критерий χ ²). Наиболее часто в таких расчетах пользуются коэффициентом со­пряженности Пирсона:

 

Значение Р всегда положительно и из­меряется от нуля до единицы. Особеннос­тью коэффициента сопряженности Пир­сона является то, что максимальное его значение всегда меньше +1 и в значительной степени зависит от количества на­блюдений (размера таблицы). В случае квадратной таблицы (k ´ k)

 

Так, в таблице размером (5 х 5) P_mах = = 0,894; в таблице (10 х 10) P_mах = 0,949. Поэтому окончательной формой выраже­ния связи между переменными с помо­щью коэффициента Пирсона является его отношение к величине Р_mах для данного случая (Р/Р_mах).

При расчете сопряженности находит применение также коэффициент Чупрова:

 

где t — число столбцов таблицы, k — чис­ло строк таблицы.

В психологической диагностике опи­санные коэффициенты используются от­носительно редко.

КОРРЕЛЯЦИЯ РАНГОВАЯ — метод корреляционного анализа, отражающий отношения переменных, упорядоченных по возрастанию их значения. Наиболее часто К. р. применяется для анализа свя­зи между признаками, измеряемыми в по­рядковых шкалах (см. Шкалы измери­тельные), а также как один из методов определения корреляции качественных признаков. Достоинством коэффициен­тов К. р. является возможность их ис­пользования независимо от характера распределения коррелирующих призна­ков.

В практике наиболее часто применя­ются такие ранговые меры связи, как ко­эффициенты К. р. Спирмена и Кендалла. Первым этапом расчета коэффициентов К. р. является ранжирование рядов переменных. Процедура ранжирования начи­нается с расположения переменных по возрастанию их значений. Разным значе­ниям присваиваются ранги, обозначае­мые натуральными числами. Если встречаются несколько равных по значению пе­ременных, им присваивается усреднен­ный ранг (табл. 12).

 

Таблица 12

Ранжирование распределения показателей теста (л = 18)

 

 

В табл. 13 приведены данные для рас­чета коэффициентов К. р. Во второй гра­фе представлены ранжированные пока­затели по первому из сравниваемых рас­пределений (оценка IQ, в третьей гра­фе — соответствующие им данные теста зрительной памяти).

 

Таблица 13