
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства энергетических спектров случайных процессовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. 2.
На этом свойстве основано понятие одностороннего энергетического спектра, существующего только в области положительных частот
3. 4. 5. Нормированный энергетический спектр
Примеры энергетических спектров некоторых стационарных СП:
1. Квазибелый шум NF (t) Энергетический спектр такого процесса (
2. Белый шум N (t) Энергетический спектр белого шума ( Корреляционная функция белого шума (рис. 4.6)
здесь использовано одно из определений дельта-функции
3. Синхронный телеграфный сигнал X (t)
Вычислим корреляционную функцию СТС, исходя из ее определения
где
В силу стационарности и при Р (0) = Р (1) = 0,5 имеем
Далее учтем, что произведение
где Р (0/0), Р (0/1), Р (1/0) и Р (1/1) – переходные вероятности передачи символов в соседних тактовых интервалах, которые будем считать одинаковыми. Таким образом
где
По полученной корреляционной функции несложно рассчитать энергетический спектр синхронного телеграфного сигнала (4.2)
Контрольные вопросы
1. Дайте определение случайного процесса (СП). 2. Каким образом дают исчерпывающее описание произвольного СП? 3. Каков смысл и размерность n -мерной функции распределения СП? 4. Каков смысл и размерность n -мерной плотности вероятности СП? 5. Как связаны функция распределения и плотность вероятности между собой? 6. Дайте определение математическому ожиданию СП и укажите его размерность и сущность как математического объекта. 7. Дайте определение дисперсии СП и укажите ее размерность и сущность как математического объекта. 8. Как осуществляют центрирование СП? 9. Определите функцию корреляции СП. 10. Какие СП называют стационарными в широком и узком смыслах? 11. Какие СП называют эргодическими? 12. Дайте определение постоянной составляющей СП, укажите ее размерность и сущность как математического объекта. 13. Дайте определение мощности СП, укажите ее размерность и сущность как математического объекта. 14. Какие СП называют нормальными (гуссовскими)? 15. Что понимают под временем корреляции СП? 16. Укажите основные свойства корреляционной функции стационарных СП? 17. Дайте определение спектральной плотности энергии СП и укажите ее размерность. 18. Дайте определение спектральной плотности мощности (энергетическому спектру) СП и укажите ее размерность. 19. Каковы связи между корреляционной функцией и энергетическим спектром стационарных СП? 20. Укажите основные свойства энергетического спектра стационарных СП. 21. Какой СП называют белым шумом? Укажите основные его свойства. 22. Какой СП называют квазибелым шумом? Укажите основные его свойства. 23. Какой СП называют синхронным телеграфным сигналом? Какова его корреляционная функция? 24. Как выглядит энергетический спектр синхронного телеграфного сигнала?
Рекомендации по проведению экспериментальных
|
|||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 614; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.156.26 (0.008 с.) |

 , что непосредственно следует из его определения (4.1). Из этого факта и соотношения (4.3) вытекает важное следствие для корреляционной функции
, что непосредственно следует из его определения (4.1). Из этого факта и соотношения (4.3) вытекает важное следствие для корреляционной функции  – она является положительно определенной, т.е. имеет неотрицательное преобразование Фурье.
– она является положительно определенной, т.е. имеет неотрицательное преобразование Фурье. – четная функция.
– четная функция.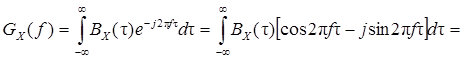
 .
.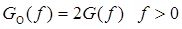 .
.

 ,
, .
. ) равномерен в ограниченной полосе частот (– F, + F) (рис. 4.3).
) равномерен в ограниченной полосе частот (– F, + F) (рис. 4.3). Корреляционная функция квазибелого шума имеет вид (рис. 4. 4)
Корреляционная функция квазибелого шума имеет вид (рис. 4. 4)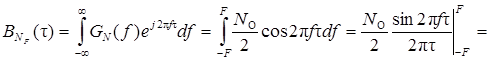
 .
. Из полученного результата вытекает некоррелированность отсчетов квазибелого шума, взятых через интервалы времени k /2 F. Для нормального процесса эти отсчеты оказываются еще и независимыми.
Из полученного результата вытекает некоррелированность отсчетов квазибелого шума, взятых через интервалы времени k /2 F. Для нормального процесса эти отсчеты оказываются еще и независимыми. ,
, .
.
 Из этих результатов вытекает статистическая независимость любых сколь угодно близких сечений такого процесса и его неограниченная дисперсия (мощность)
Из этих результатов вытекает статистическая независимость любых сколь угодно близких сечений такого процесса и его неограниченная дисперсия (мощность)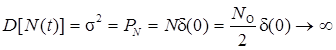 .
.
 Синхронный телеграфный сигнал (CТС) представляет собой стационарный дискретный случайный процесс, принимающий на тактовых интервалах длительностью Т значения + h с вероятностью Р (0) или – h с вероятностью Р (1). Возможная реализация такого процесса показана на рис. 4.7.
Синхронный телеграфный сигнал (CТС) представляет собой стационарный дискретный случайный процесс, принимающий на тактовых интервалах длительностью Т значения + h с вероятностью Р (0) или – h с вероятностью Р (1). Возможная реализация такого процесса показана на рис. 4.7. ,
, .
. =
=  = 0 и
= 0 и
 , если
, если  , где
, где  временной интервал от сечения t 1 до ближайшей границы такта (сечения принадлежат одному тактовому интервалу). В противном случае (при
временной интервал от сечения t 1 до ближайшей границы такта (сечения принадлежат одному тактовому интервалу). В противном случае (при  )
) ,
, ,
, – плотность вероятности временного интервала
– плотность вероятности временного интервала  .
.


 .
. Графики корреляционной функции и энергетического спектра синхронного телеграфного сигнала приведены на рис. 4.8.
Графики корреляционной функции и энергетического спектра синхронного телеграфного сигнала приведены на рис. 4.8.


