Свойства объектов регулирования

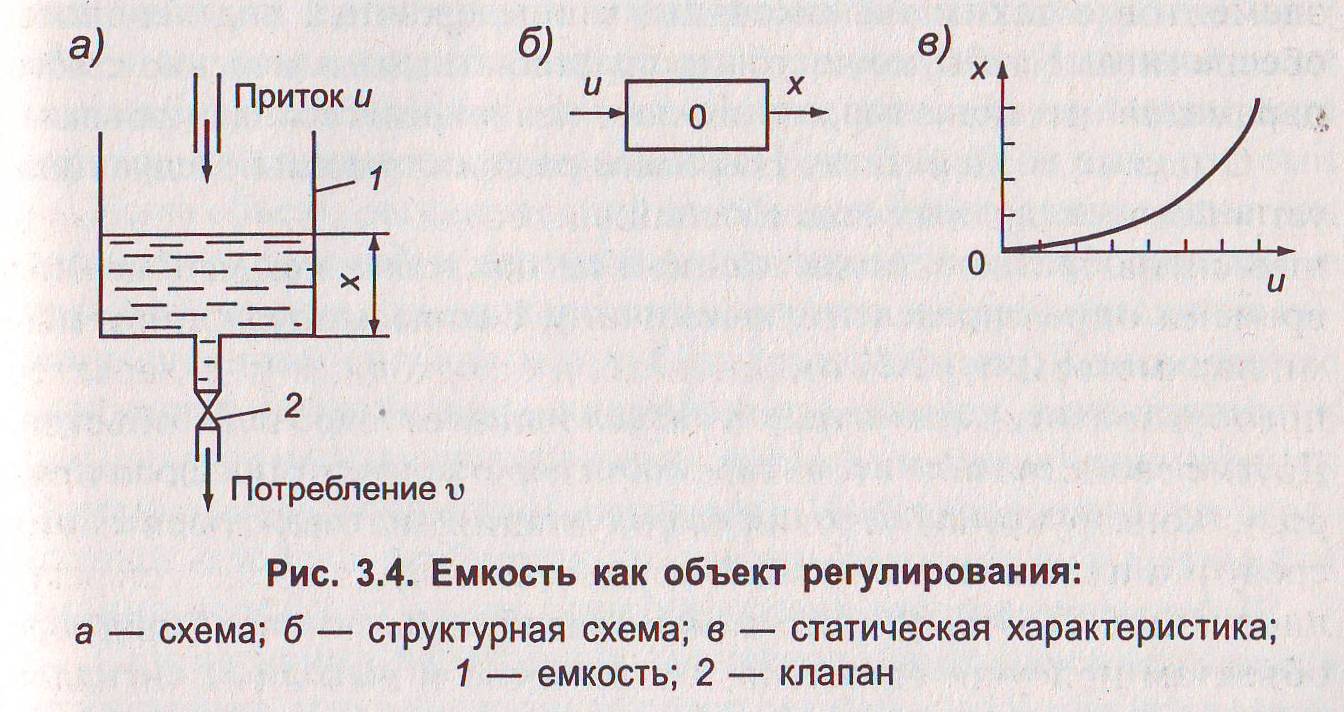
Объект регулирования является элементом АСР, и свой­ства всей системы во многом определяются свойствами объекта. Изучение свойств объектов регулирования — важный и часто основной этап разработки АСР. Объект регулирования в отличие от остальных элементов АСР является заранее заданным элементом, свойства которого определяются его значением в технологическом процессе. Поэтому создание АСР сводится к подбору остальных элементов с такими свойствами, чтобы свойства всей системы обеспечивали требуемую точность стабилизации регулируемого параметра, что невозможно сделать без знания свойств объекта.

С позиций теории регулирования объект рассматривают как устройство, преобразующее по определенному закону свои вход­ные сигналы в выходные. Состояние объекта в каждый момент времени определяется его выходными сигналами (регулируемы­ми параметрами), зависимость которых от входных (т. е. характер преобразования сигналов) и обусловливает свойства объекта. Другие свойства объектов, характеризующие их физическую при­роду, конструкцию, условия эксплуатации, находящуюся в них среду и т. п., как указывалось, несущественны для процессов регу­лирования. Поэтому часто самым различным по своей природе объектам присущи одинаковые зависимости выходных сигналов от входных.

Как было показано в разд. 3.1, при управлении инженерными системами их разбивают на элементарные объекты регулирова­ния, как правило, с одним регулируемым и одним регулирующим параметрами. Управление такими объектами осуществляется одно­контурными АСР. Поэтому здесь будут рассматриваться свойства только объектов регулирования с одним выходным сигналом.

Принято различать статические и динамические свойства объектов регулирования. Статические свойства объекта — это его свойства в установившемся состоянии (в статике), т. е. при неиз­меняющихся входном и выходном сигналах. При этом зависи­мость установившегося значения выходного сигнала от входного называется статической характеристикой объекта.

В качестве примера рассмотрим статическую характеристику емкости 1 с притоком и потреблением жидкости, выходным сиг­налом которой является уровень (рис. 3.4, а). На линии потреб­ления установлен клапан 2 с постоянным проходным сечением, а после клапана происходит свободный слив жидкости. В этом случае расход на потреблении и уже не является входным сигна­лом объекта, как для емкости на рис. 3.2, так как он не может изменяться произвольно, а зависит от уровня в емкости х, т. е. от выходного сигнала. Из гидравлики известно, что эта зависимость имеет вид

υ= (3.1)

где k — коэффициент пропорциональности, зависящий от про­пускной способности клапана.

Таким образом, в данном примере объект имеет один входной сигнал — расход на притоке и и один выходной — уровень в емкости х (рис. 3.4, б). В состоянии равновесия объекта приток и потребление должны быть одинаковы и постоянны. Следова­тельно, заменяя в формуле (3.1) υ на и и решая это уравнение относительно х, получим зависимость установившегося значения уровня х от постоянного расхода на притоке и, т. е. статическую характеристику объекта:

х = и² / k² (3.2)

Эта статическая характеристика приведена на рис. 3.4, в.

Как отмечалось, в реальных условиях любой объект регулиро­вания подвержен воздействию случайных возмущений и поэтому всегда находится в неустановившемся состоянии. Следовательно, статическая характеристика объекта регулирования не может пол­ностью характеризовать его поведение в реальных условиях. С помощью этой характеристики можно определить лишь стати­ческую ошибку АСР. Поведение же объекта в неустановившемся состоянии (в динамике) зависит от его динамических свойств.

Динамические свойства объекта проявляются только при изме­нении его входных сигналов. При этом и выходной сигнал будет изменяться во времени. Причем в зависимости от характера изме­нения входных сигналов выходной сигнал одного и того же объекта может изменяться по-разному. Поэтому для характеристики дина­мических свойств объекта нельзя построить зависимость выходного параметра от входного, аналогичную статической характерис­тике. Для выявления динамических свойств объекта необходимо узнать его реакцию на какой-либо определенный вид входного воздействия. Чтобы можно было сравнивать динамические свой­ства различных объектов, применяют одинаковые стандартизован­ные входные воздействия. Наиболее распространены следующие два вида стандартных воздействий:

• скачкообразные, когда входной сигнал изменяют мгновенно, скачком на определенную величину, а затем поддерживают по­стоянным (рис. 3.5, а);

• импульсные, когда входной сигнал изменяют на очень большую величину в течение очень короткого промежутка времени, а затем возвращают к прежнему значению; такая форма воз­действия имеет вид импульса (рис. 3.5, б).

До подачи стандартного воздействия объект должен находиться в состоянии равновесия, т. е. его входной и выходной сигналы должны быть постоянными во времени. Зависимость выходного сигнала объекта во времени начиная с момента подачи стандарт­ного воздействия называется динамической характеристикой или переходным процессом. Графики типичных переходных процессов

в промышленных объектах регулирования при скачкообразном входном воздействии приведены на рис. 3.6, где через х обозна­чен выходной сигнал, а через t — время.

Рассмотрим для примера переходный процесс в емкости с при­током и потреблением жидкости (см. рис. 3.5). До подачи стан­дартного воздействия по расходу на притоке объект находится в состоянии равновесия: приток и потребление одинаковы. Увели­чим расход на притоке скачком (см. рис. 3.6, а). Тогда в емкости начнется накопление жидкости и уровень в ней будет возрастать. Скорость роста уровня зависит от разности расходов на притоке и потреблении υ — и, и она тем больше, чем больше эта разность. С другой стороны, с ростом уровня в емкости сразу же начнется и увеличение расхода и через клапан в соответствии с формулой (3.1). Следовательно, разность расходов на притоке и потреблении будет уменьшаться, а рост уровня замедляться. Увеличение уровня пре­кратится, когда потребление снова сравняется с притоком и тем самым будет достигнуто новое состояние равновесия. Описанный переходный процесс x(t) показан на рис. 3.6, б.

Если объект регулирования имеет несколько входных сигна­лов (регулирующий и возмущающие параметры), то переходные процессы в нем при подаче стандартного воздействия по каж­дому входному сигналу могут быть различными. В этом случае различают воздействия, поданные по каналу регулирования (изменяется регулирующий параметр) или по каналу возмущения (изменяется возмущающий параметр). Наиболее интересен пере­ходный процесс в объекте по каналу регулирования, так как именно через этот канал осуществляется прямая связь в АСР.

При изучении переходных процессов необходимо принимать во внимание, что всегда существуют реальные возмущающие воз­действия, вызывающие случайные колебания выходного сигнала объекта. Чтобы четко выявить переходный процесс на фоне слу­чайных колебаний, стандартные воздействия, очевидно, должны быть значительно более сильными, чем случайные воздействия на объект. Именно по этой причине стандартные воздействия имеют вид скачка или импульса, т. е. мгновенно, а значит и наиболее резко, изменяются входные сигналы. Величину скачкообразного или импульсного воздействия выбирают такой, чтобы, с одной стороны, получить заметный переходный процесс, а с другой — не допустить возникновения аварийного режима работы. Пере­ходные процессы являются универсальным средством изучения динамических свойств объектов. Чтобы понять, как в переход­ном процессе проявляются динамические свойства объекта и как

 

их можно установить по виду процесса, рассмотрим типичные динамические свойства объектов и соответствующие им переход­ные процессы.

Почти все объекты регулирования обладают инерцией, кото­рая проявляется в том, что при мгновенном изменении входного сигнала выходной сигнал изменяется не мгновенно, а постепенно. Изменение выходного сигнала продолжается и после прекращения входного воздействия, т. е. когда входной сигнал уже не изменяется. Такое явление называется последействием. Примеры графиков переходных процессов для инерционных объектов показаны на рис. 3.6, б, в.

Инерция присуща объектам и протекающим в них процессам самой различной природы. Например, постепенное изменение уровня в емкости после скачкообразного или импульсного изме­нения притока жидкости — проявление гидродинамической инер­ции. У некоторых объектов инерция может быть пренебрежимо малой в сравнении с остальными элементами САР и не оказывает заметного влияния на процесс регулирования. Такие объекты называют безынерционными. В идеальном безынерционном объекте выходной сигнал изменяется синхронно с входным без всякого последействия, как показано на рис. 3.6, г. Инерция реальных объектов регулирования вызвана наличием в них запаса вещества или энергии. Чем. больше этот запас, тем сильнее проявляется инерция объекта. Так, инерция емкости обусловлена запасом жидкости в ней. Способность объекта накапливать вещество или энергию называется емкостью и является количественной мерой инерции.

При переходных процессах в инерционных объектах запас вещества или энергии в них может изменяться как монотонно (только увеличиваться или только уменьшаться), так и колеба­тельно. Например, груз, подвешенный на пружине, при отклоне­нии его от положения равновесия начинает колебаться. Такой же колебательный характер имеет величина тока в электрическом колебательном контуре.

Общим для этих примеров является колебательный характер выходных сигналов объектов — положения груза и тока в элект­рическом контуре. Объекты, обладающие таким свойством, назы­ваются колебательными. В отличие от них объекты с монотонным изменением выходных сигналов называются апериодическими (неколебательными). Примеры переходных процессов в аперио­дических объектах регулирования приведены на рис. 3.6, б, в, в колебательном объекте — на рис. 3.6, д.

Еще одним важным свойством реальных объектов является запаздывание. Оно проявляется в том, что реакция объекта на входное воздействие, т. е. изменение его выходного сигнала, за­паздывает по отношению к изменению входного сигнала. График переходного процесса с запаздыванием приведен на рис. 3.6, е.

Мы рассматривали объекты регулирования, в которых пере­ходные процессы заканчиваются установившимся значением вы­ходного сигнала (пунктирная линия на рис. 3.6, б, в, д, е). Такие объекты под влиянием входного воздействия переходят из одного состояния равновесия в другое (отсюда и название процесса — переходный). Эти объекты регулирования получили название устойчивых. Все рассмотренные выше переходные процессы при­сущи устойчивым объектам.

Устойчивые объекты регулирования обладают одним общим свойством — самовыравниванием, т. е. способностью переходить из одного установившегося состояния в другое по окончании переходного процесса при скачкообразном входном воздействии. Чем меньше изменяется выходной сигнал в переходном процессе при одном и том же скачкообразном входном воздействии, тем больше степень самовыравнивания объекта. Существуют устойчивые объекты с очень большим самовыравниванием, когда вы­ходной сигнал после переходного процесса почти не отличается; от его начального значения. График статической характеристики таких объектов расположен почти горизонтально, т. е. в установившемся состоянии выходной сигнал очень слабо зависит от вход­ного. В инженерных системах зданий имеются объекты и с очень малым самовыравниванием, когда малейшее изменение входного / сигнала вызывает значительное изменение выходного сигнала.

Устойчивость — широко распространенное в строительстве, но не обязательное свойство объектов: существуют и неустойчивые объекты регулирования. У таких объектов состояние равновесия существует, но оно неустойчиво, поэтому любое сколь угодно малое воздействие выводит неустойчивый объект из состояния равновесия и с течением времени он все больше отклоняется oт этого состояния. Переходный процесс в неустойчивом объекте показан на рис. 3.6, ж.

Неустойчивые объекты довольно редки. Значительно чаще встречаются так называемые нейтральные объекты, занимающие; промежуточное положение между устойчивыми и неустойчивыми. Свойства нейтрального объекта рассмотрим сначала на примере. Нейтральный объект можно получить из рассмотренной выше емкости с притоком и потреблением жидкости, если расход на потреблении сделать независимым от уровня в емкости. Для этого достаточно, например, установить на линии потребления насос с постоянной производительностью (см. рис. 3.2). У такого объекта существует состояние равновесия: когда приток равен потребле­нию, уровень не изменяется. Однако в отличие от устойчивого объекта (емкости с клапаном на линии потребления — см. рис. 3.4) равенство притока и потребления может соблюдаться при любом значении уровня. Иначе говоря, в состоянии равновесия объекта его выходной сигнал — уровень — может быть любым независимо от расхода на притоке и потреблении, т. е. статической характе­ристики у такого объекта нет. Поэтому нейтральные объекты назы­вают еще астатическими.

Приложим теперь скачкообразное воздействие к расходу на притоке, например увеличим его. Так как потребление не зависит от уровня в емкости, то разность между притоком и потреблением будет оставаться постоянной и, следовательно, уровень в емкости' будет возрастать с постоянной скоростью, не стремясь ни к какому установившемуся значению. График такого переходного процесса приведен на рис. 3.6, з. Подобные свойства присущи всем нейт­ральным объектам. О нейтральных объектах можно сказать, что они не имеют самовыравнивания.

Проанализируем теперь, как рассмотренные динамические свойства объектов проявляются в соответствующих переходных процессах. Наиболее широко распространенное свойство инерции объектов в инженерных системах, как устойчивых, так нейтральных и неустойчивых, проявляется в переходном процессе в виде плав­ного, без скачков изменения выходного сигнала (рис. 3.6, б, в, д, ж, з). Следствием такого поведения инерционного объекта явля­ется последствие, т. е. изменение выходного сигнала при уже не изменяющемся (после скачка) входном сигнале. Количественно инерцию объекта можно было бы охарактеризовать скоростью изменения выходного сигнала. Однако, как видно из рис. 3.6, эта скорость изменяется с течением времени, причем у одних объ­ектов она максимальна в начальный момент времени (рис. 3.6, б), а у других — в некоторой точке а (рис. 3.6, в).

Определение максимальной скорости переходного процесса позволяет ввести понятие постоянной времени, которая и служит оценкой инерции объекта. Постоянной времени Т объекта назы­вается время, за которое его выходной сигнал х достиг бы устано­вившегося значения в переходном процессе, если бы изменялся все время с максимальной скоростью. Как следует из определения, постоянная времени существует только у устойчивых объектов. Ее величину можно найти по графику переходного процесса. Для этого следует провести касательную к этому графику в точке максимальной скорости. Тогда постоянную времени Т находят, как показано на рис. 3.6, б, в. Такой способ обычно используется только для апериодических (неколебательных) объектов.

С точки зрения управления инерция объектов имеет как поло­жительную, так и отрицательную сторону. Положительная состоит в том, что благодаря инерционности объект не успевает реагиро­вать на кратковременные возмущения, что облегчает стабилизацию его регулируемого параметра. С другой стороны, неизбежное при этом последействие затрудняет компенсацию возмущений в АСР по отклонению, что снижает качество стабилизации технологи­ческих параметров.

Свойство колебательности объектов играет только отрицатель­ную роль в процессе регулирования. Вследствие колебательности выходной сигнал объекта изменяется в течение переходного про­цесса на большую величину, чем в апериодическом объекте. Это видно из сравнения графиков переходных процессов в апериоди­ческом (рис. 3.6, б, в) и колебательном (рис. 3.6, д) объектах.

Запаздывание в объектах регулирования проявляется в сдвиге по времени начала переходного процесса относительно входного воздействия. Величина этого временного сдвига называется временем запаздывания, а само запаздывание — чистым или транс­портным. При транспортном запаздывании выходной сигнал х совсем не изменяется в течение всего времени запаздыванияτ_Т(рис. 3.6, е). Однако эффект, похожий на запаздывание, наблюда­ется и в некоторых объектах без транспортного запаздывания, когда выходной сигнал х в переходном процессе сначала изменя­ется медленно (см. рис. 36, в). Такой эффект кажущегося запазды­вания называется переходным запаздыванием. Время переходного, запаздывания τ_П можно найти по графику переходного процесса, как показано на рис. 3.6, в.

Запаздывание, в особенности транспортное, является наиболее неблагоприятным свойством объектов с точки зрения их регулиро­вания. Действительно, в АСР с обратной связью рассогласование, вызываемое возмущающими воздействиями на объект с запазды­ванием, проявляется лишь по истечении времени запаздывания. Поэтому и регулирующее воздействие в таких АСР запаздывает по отношению к возмущающим воздействиям. Получается, что регулятор в АСР реагирует не на текущее, а на прошлое возмуще­ние, что затрудняет его компенсацию и приводит к ухудшению стабилизации регулируемого параметра. По этой же причине объекты, имеющие переходное запаздывание, труднее поддаются регулированию.

Как правило, запаздывание обычно сочетается с инерцией. Наиболее трудные для регулирования безынерционные объекты с транспортным запаздыванием встречаются редко. Установлено, что для объектов с запаздыванием качество регулирования может быть лучше при меньшем отношении времени полного запаз­дывания τ= τ_П + τ_Т к постоянной времени Т. Отношениеτ/ Т минимально (равно нулю) для всех объектов без запаздывания и максимально (бесконечно велико) для безынерционных с за­паздыванием, когда Т= 0.

Устойчивые объекты легче поддаются управлению, чем не­устойчивые. Так, в любом устойчивом объекте отклонение регу­лируемого параметра под действием возмущения имеет вполне' определенную, не бесконечную величину (рис. 3.6, б-е). Поэтому при достаточно большом самовыравнивании, когда возмущающие воздействия вызывают малые колебания регулируемого параметра, можно обойтись без системы управления. В нейтральных же объектах, в особенности в неустойчивых, отклонение регулиру­емого параметра под действием возмущений с течением времени может стать сколь угодно большим. Поэтому управлять такими объектами, безусловно, необходимо. Таким образом, самовырав­нивание объекта способствует управлению им и поэтому иногда называется саморегулированием.

Степень самовыравнивания, как отмечалось, характеризует запас устойчивости объекта. Объекты с большим самовыравнива­нием имеют большой запас устойчивости и легко поддаются управ­лению. Объекты с нулевым самовыравниванием, т. е. нейтраль­ные, не имеют запаса устойчивости (говорят, что они находятся на границе устойчивости). Неустойчивые же объекты обладают отрицательным самовыравниванием, и им приписывают отрица­тельный запас устойчивости.

Следует иметь в виду, что степень самовыравнивания не пол­ностью характеризует объект с точки зрения регулирования. Имеют значение и другие показатели, в частности отношениеτ/ Т. Так, для объекта с большим отношениемτ / Т качество стабилиза­ции его регулируемого параметра в АСР может быть низким даже при значительном самовыравнивании.

 

 

КАЧЕСТВО РЕГУЛИРОВАНИЯ

Свойства объекта регулирования всегда определяются его значением в инженерной системе, но не всегда благоприятны для управления. Поэтому задачей управления объектом можно счи­тать изменение его свойств для уменьшения чувствительности к возмущающим воздействиям. С этой точки зрения АСР в целом можно рассматривать как объект, входными сигналами которого являются задания х _зад и возмущение υ, а выходным сигналом — регулируемый параметр х (рис. 3.7). Этот объект, оче­видно, должен обладать лучшими стати­ческими и динамическими свойствами чем сам объект регулирования.

Как и для объектов регулирования, для АСР также различают статические и динамические показатели. Основным статическим показателем АСР является статическая ошибка, т. е. рассогласование в установившемся состоянии. Как известно, в астатическом АСР статическая ошибка отсутствует» Поэтому можно утверждать, что астатический регулятор наилуч­шим образом корректирует статические свойства объекта.

Динамические показатели АСР проявляются только в неуста­новившемся состоянии. Поэтому их можно выявить по реакции АСР на стандартные воздействия по каналам задания х _зад или возмущения и, т. е. по переходным процессам в ней. Примеры; переходных процессов в АСР — изменение рассогласования при скачкообразном воздействии по каналу задания (на значение Δ х _зад) и каналу возмущения — приведены на рис. 3.8.

Какие свойства АСР являются идеальными с точки зрений качества стабилизации параметра? В идеальной АСР любые возмущающие воздействия (в том числе и стандартные) не должны

 

вызывать рассогласования. Это означает, что идеальная АСР дол­жна быть нечувствительной к возмущениям. Отсюда следует, что в идеальной АСР статическая ошибка отсутствует, а переходный процесс таков, что площадь, заштрихованная на рис. 3,8, равна нулю.

Идеальные переходные процессы в реальных АСР практически недостижимы. По отклонению переходного процесса в реальной АСР от идеального можно судить о качестве ее. работы. Для коли­чественной оценки качества работы АСР служат показатели ка­чества регулирования (качества переходных процессов). Одним из таких показателей в установившемся состоянии АСР является статическая ошибка. Наиболее универсальный динамический показатель, характеризующий близость АСР к идеальной, — абсолютное значение площади переходного процесса (на рис. 3.8, а эта площадь заштрихована). Наряду с абсолютной величиной площади переходного процесса часто используют такой показа­тель, как квадрат этой площади (при этом автоматически не учи­тывается знак отклонения). Оба эти показателя характеризуют одновременно и величину, и длительность рассогласования в пе­реходном процессе. Иногда важнее длительность переходного про­цесса, в частности когда требуется перевести объект управления в новое состояние за минимальное время (например, при ава­рийном сбросе давления). В этом случае за показатель качества регулирования принимают время переходного процесса t _П.

В некоторых случаях главную роль играет величина рассогла­сования в переходном процессе. Тогда показателем качества регу­лирования считают максимальное рассогласование Δ х _mах, назы­ваемое динамической ошибкой. В реальных условиях лучше вводить стандартное воздействие Δ х _зад по каналу задания. Такие переход­ные процессы характеризуются теми же показателями качества, за исключением динамической ошибки. Вместо нее вводят другой показатель — перерегулирование Δ х _п, определяемый, как показано на рис. 3.8, а. Указанные показатели качества равны нулю для идеальной АСР и больше нуля для любой реальной АСР. Чем эти показатели меньше, тем ближе АСР к идеальной.

Свойства любой АСР, а следовательно, и качество переходных процессов в ней зависят как от свойств объекта, так и от характе­ристик остальных элементов АСР. Поэтому, изменяя характерис­тики отдельных элементов АСР, в частности регулятора, можно добиться наилучшего возможного и данных условиях качества переходного процесса (например, минимального времени). Такая АСР будет наилучшей из всех возможных для данного объекта регулирования, и ее называют оптимальной. Не следует смешивать понятия оптимальности и идеальности. Идеальная АСР практи­чески недостижима, а оптимальная — это наилучшее приближение к идеальной.

Разработка и построение оптимальных АСР обычно связаны со значительными трудностями, а сами эти АСР оказываются сложными и дорогими. Однако замечено, что даже большие отступ­ления от оптимальной АСР обычно приводят к незначительному ухудшению качества регулирования. Такие отступления практи­чески неизбежны, так как, во-первых, свойства, как правило, известны лишь приближенно и изменяются с течением времени; во-вторых, при изготовлении регуляторов и других элементов АСР неизбежен разброс их параметров. Поэтому в большинстве; случаев требуется наладка АСР на действующем объекте. С этой целью регуляторы снабжают органами регулировки, позволяющими изменять их настройку в достаточно широком диапазоне.

Наладка АСР на действующем объекте требует высокой квали­фикации. Регулируемый параметр АСР под действием случайных возмущений колеблется около своего задания. В этих условиях трудно проследить влияние параметров настройки регулятора на показатель качества и определить, в какую сторону и насколько следует их изменять. Ясно, что чем меньше параметров настройки, тем проще процесс наладки АСР. Однако сложные современные АСР — комбинированные, многоконтурные — могут иметь достаточно много параметров настройки. И в этом случае бессильны опыт и интуиция самого квалифицированного специалиста.

Системы, способные автоматически находить и поддерживать оптимальные значения параметров настройки, называются само- настраивающимися. Такие системы содержат элементы (устройства), автоматически изменяющие параметры настройки в нужную; сторону. Иначе говоря, самонастраивающиеся АСР автоматически изучают свойства объекта и возмущающих воздействий и приспосабливаются к ним. Автоматические системы, обладающие способностью к самообучению (помимо основной их функции — управления), называются самообучающимися или адаптивными. Самонастраивающиеся АСР — лишь один из видов адаптивных! систем. Другим частным случаем адаптивных систем являются так^: называемые экстремальные, которые не только стабилизируют^: регулируемый параметр около его заданной величины, но и автоматически выбирают задание, наилучшее (оптимальное) для всей инженерной системы.