
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства согласованных фильтровСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Импульсная характеристика СФ является «зеркальным отражением» сигнала, с которым он согласован, относительно момента времени 0,5 t 0 (с точностью до постоянного коэффициента)
Это свойство было положено в основу определения СФ (6.15).
2. Передаточная функция СФ
После замены t 0 – t = t, t = t 0 – t, dt = – d t, при t ® ¥ t ® -¥
Таким образом, передаточная функция СФ с точностью до множителя
Амплитудно-частотная характеристика СФ
с точностью до коэффициента а повторяет амплитудный спектр сигнала, с которым он согласован Фазо-частотная характеристика СФ
отличается знаком от фазового спектра сигнала, с которым он согласован (без учета слагаемого –ω t 0).
3. Форма отклика СФ на «свой» сигнал (сигнал с которым он согласован)
Учитывая, что из (6.15) вытекает
Таким образом, отклик СФ на «свой» сигнал с точностью до коэффициента совпадает с его корреляционной функцией, смещенной по оси времени на интервал t 0 (рис. 6.7)
Из полученного результата вытекают следующие выводы: · Отклик СФ на «свой» сигнал с точностью до постоянного коэффициента совпадает с его корреляционной функцией. · Длительность отклика на «свой» сигнал всегда равна 2 Т. · СФ не восстанавливает форму сигнала, искаженного шумом. Его задача создать один отсчет y (t 0), по которому можно наилучшим образом судить о присутствии на входе «своего» сигнала.
4. СФ обеспечивает наибольшее отношение сигнал/шум (с/ш) на своем выходе при действии на входе аддитивной смеси «своего» сигнала и центрированного нормального белого шума Докажем это, уточнив предварительно, что под отношением с/ш на выходе СФ понимают отношение математического ожидания отсчета случайной реакции СФ Y (t) в момент времени t 0 = T к корню из ее дисперсии
Рассмотрим произвольный линейный фильтр с передаточной функцией
Полученное выражение представляет собой не что иное, как скалярное произведение
Вычислим дисперсию случайной величины
имеем
Наибольшее значение с/ш (равенство в полученном выражении) достигается при совпадении векторов Найдем саму величину отношения с/ш на выходе СФ при действии на его входе «своего» сигнала
где Е – энергия «своего» сигнала, N О – односторонняя спектральная плотность мощности шума,
Таким образом, максимальное отношение с/ш на выходе СФ определяется энергией «своего» сигнала, независимо от его формы. Определим отношение с/ш по мощности
где F K – ширина полосы пропускания канала. При совпадении ширины полосы пропускания канала с шириной спектра сигнала F K = Fs имеем
Отсюда вытекает целесообразность выбора сигналов с большой базой 2 FsT для передачи дискретных сообщений, что позволяет увеличить отношение с/ш при согласованной фильтрации.
Согласованная фильтрация и корреляционный прием Некоторых типичных сигналов Рассмотрим особенности когерентного приема некоторых сигналов и реализации соответствующих согласованных фильтров. Прямоугольные видеоимпульсы Сигнал в виде прямоугольного видеоимпульса s (t) (рис. 6.8,а) и импульсная характеристика g СФ(t) согласованного с ним фильтра (рис. 6.8,б) описываются выражениями
Вычислим передаточную функцию СФ
Сомножитель Реакция СФ на прямоугольный импульс показана на рис. 6.8,в. Для сравнения на рис. 6.8,г показана реакция на тот же сигнал коррелятора (рис. 6.10).
Прямоугольные радиоимпульсы Сигнал в виде прямоугольного радиоимпульса s (t) описывается выражением
Импульсная характеристика g СФ(t) согласованного с ним фильтра на интервале
Такого рода импульсной характеристикой обладает колебательный контур с добротностью Q ® ¥, однако, у него она продолжается во времени неограниченно. Для «гашения» импульсной характеристики (реакции контура на воздействие d(t)) в момент t=T можно воспользоваться соответствующей коммутацией контура (рис. 6.11,а) или вычитанием самой задержанной на T реакции (рис. 6.11,б). Прямоугольные радиоимпульсы и реакции на них СФ и коррелятора можно видеть на рис. 6.12, 6.19, 6.20 и 6.21.
Сложные двоичные сигналы
Синтез СФ для сложного двоичного сигнала произведем, отталкиваясь от его импульсной характеристики (рис. 6.13,б). Видно, что требуемую форму Проанализируем импульсную характеристику ТФ со стороны входа А, как его реакцию на воздействие в виде d-функции. Поданная этот вход d-функция (рис. 6.15,а) появится на отводах ЛЗ с соответствующими задержками и после суммирования в сумматоре (с учетом полярности) создаст последовательность, показанную на рис. 6.15,б. На выходе СФП, согласованного с одиночным П-импульсом длительностью Из двоичных n -последовательностей наибольший интерес представляют собой последовательности (коды) Баркера. Они обладают важным свойством
где В БОК – величина боковых лепестков корреляционной функции, В (0) – начальное значение корреляционной функции. Показанная на рис. 6.14 двоичная последовательность как раз и является кодом Баркера при n = 7. Импульсную характеристику и реакцию фильтра, согласованного с семиэлементным кодом Баркера, на этот «свой» сигнал (смещенную на Т корреляционную функцию кода Баркера) можно видеть на рис. 6.22.
Согласно теореме Котельникова сигналы с ограниченным частотой F спектром точно передаются последовательностью своих отсчетов, взятых через интервалы
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 2167; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.146.108 (0.008 с.) |

 .
. .
.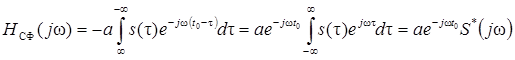 .
. совпадает с сопряженной спектральной функцией сигнала, с которым он согласован
совпадает с сопряженной спектральной функцией сигнала, с которым он согласован .
.

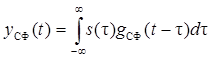 .
. , получим
, получим .
. .
.
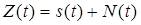 со спектральной плотностью мощности N=N О/2.
со спектральной плотностью мощности N=N О/2. . (6.16)
. (6.16) . Поскольку
. Поскольку 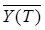 представляет собой отсчет реакции ys (T) на математическое ожидание воздействия, каковым является сигнал s (t), то
представляет собой отсчет реакции ys (T) на математическое ожидание воздействия, каковым является сигнал s (t), то .
. двух векторов
двух векторов 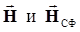 в комплексном пространстве Гильберта, если иметь в виду следующие соответствия:
в комплексном пространстве Гильберта, если иметь в виду следующие соответствия: .
. Подставляя полученные результаты в выражение (6.16) и применяя неравенство Коши-Буняковского-Шварца
Подставляя полученные результаты в выражение (6.16) и применяя неравенство Коши-Буняковского-Шварца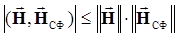 ,
, .
. , т. е. для случая использования СФ, что и требовалось доказать. Это чрезвычайно важное свойство некоторые авторы закладывают в основу определения СФ.
, т. е. для случая использования СФ, что и требовалось доказать. Это чрезвычайно важное свойство некоторые авторы закладывают в основу определения СФ. , (6.17)
, (6.17) .
. ,
,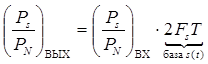 .
.
 .
. представляет собой передаточную функцию интегратора, вычитаемое
представляет собой передаточную функцию интегратора, вычитаемое  в скобках
в скобках 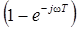 – передаточная функция элемента задержки на время Т, а сама скобка соответствует алгебраическому сумматору. В итоге приходим к схеме СФ, показанной на рис. 6.9.
– передаточная функция элемента задержки на время Т, а сама скобка соответствует алгебраическому сумматору. В итоге приходим к схеме СФ, показанной на рис. 6.9.



 .
.


 Рассмотрим сигналы в виде n -последовательностей импульсов прямоугольной формы положительной и отрицательной полярности с фиксированным размахом. Возможный вид такого сигнала при n = 7 показан на рис. 6.13,а. Усложнение сигнала объясняется желанием получить определенную (острую) форму отклика на выходе согласованного с ним фильтра и повысить отношение с/ш. Поскольку
Рассмотрим сигналы в виде n -последовательностей импульсов прямоугольной формы положительной и отрицательной полярности с фиксированным размахом. Возможный вид такого сигнала при n = 7 показан на рис. 6.13,а. Усложнение сигнала объясняется желанием получить определенную (острую) форму отклика на выходе согласованного с ним фильтра и повысить отношение с/ш. Поскольку  , тем шире спектр сигнала и больше его база. Сигналы такого рода удобно использовать в радиолокационных и в асинхронно адресных телекоммуникационных системах.
, тем шире спектр сигнала и больше его база. Сигналы такого рода удобно использовать в радиолокационных и в асинхронно адресных телекоммуникационных системах. можно получить суммированием прямоугольных импульсов длительностью
можно получить суммированием прямоугольных импульсов длительностью  , сдвинутых на кратные
, сдвинутых на кратные  интервалы времени, с соответствующими полярностями. Такие импульсы можно получить «размножением» единственного исходного П-импульса длительностью
интервалы времени, с соответствующими полярностями. Такие импульсы можно получить «размножением» единственного исходного П-импульса длительностью 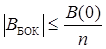 ,
, Произвольные F- финитные сигналы
Произвольные F- финитные сигналы и, следовательно, могут быть заменены ступенчатой функцией (рис. 6.16,а), которая отличается от двоичного сигнала (рис. 6.13,а) только размахами отдельных П-импульсов длительностью
и, следовательно, могут быть заменены ступенчатой функцией (рис. 6.16,а), которая отличается от двоичного сигнала (рис. 6.13,а) только размахами отдельных П-импульсов длительностью  . Отсюда вытекает возможность формирования такого рода сигналов и их согласованной фильтрации с помощью аналогового трансверсального фильтра (рис. 6.17, 6.24). Его схема отличается от схемы двоичного ТФ (рис. 6.14) только заменой фильтра, согласованного с П-ипульсом (СФП) на сглаживающий фильтр (ФНЧ с частотой верхнего среза F) и использованием в цепях отводов ЛЗ усилителей с коэффициентами усиления, пропорциональным отсчетам F- финитного сигнала.
. Отсюда вытекает возможность формирования такого рода сигналов и их согласованной фильтрации с помощью аналогового трансверсального фильтра (рис. 6.17, 6.24). Его схема отличается от схемы двоичного ТФ (рис. 6.14) только заменой фильтра, согласованного с П-ипульсом (СФП) на сглаживающий фильтр (ФНЧ с частотой верхнего среза F) и использованием в цепях отводов ЛЗ усилителей с коэффициентами усиления, пропорциональным отсчетам F- финитного сигнала.




