Исследований случайных процессов

 

Для закрепления полученных при изучении раздела 4 знаний на базе виртуальной лаборатории можно провести экспериментальные исследования случайных процессов используя:

· осциллограф – для наблюдения реализаций СП во временной области,

· анализатор спектра – для наблюдения реализаций СП в частотной области,

· анализатор уровней – для наблюдения плотности вероятности,

· коррелометр – для наблюдения корреляционных функций.

Целесообразно работать в рамках конфигурации лабораторного стола по темам работ №2 и №19. Источником СП с равномерным и нормальным распределением может служить генератор сигнала (в режиме генератора шума) (рис. 4.9) и соответствующие подпункты меню «Сигналы» (рис. 4.10).

Рекомендуется выполнить лабораторную работу №19 в полном объеме (рис. 4.10). Обратите внимание на связь размеров «шумовой дорожки» на экране осциллографа с эффективным значением шума и на связь корреляционных характеристик с энергетическими спектрами случайных процессов.

 

Прохождение случайных процессов через

Преобразователи сигналов

 

В общем случае решение задачи прохождения заданного СП через конкретную электрическую цепь – функциональный узел (ФУ) произвольной сложности предполагает определение n -мерной плотности вероятности (или функции распределения) реакции цепи Y (t) на заданное случайное воздействие X (t) (рис. 5.1). Однако общего метода решения такой задачи не существует. Поэтому ограничимся рассмотрением некоторых частных случаев.

 

Прохождение случайных процессов

Через безынерционные цепи

 

Безынерционная цепь (безынерционный функциональный узел –БФУ) полностью описывается функциональной зависимостью y = f (x), связывающей мгновенные значения воздействия x (t) и реакции y (t) в совпадающие моменты времени. В результате имеем дело с функциональным преобразованием случайного процесса Y (t) = f [ X (t)].

Для вычисления одномерной плотности вероятности реакции w (y) по известной плотности вероятности воздействия w (x) рассмотрим рис. 5.2, на котором изображены функциональная характеристика БФУ y = f (x), заданная плотность вероятности воздействия w (x) и искомая плотность вероятности реакции БФУ w (y). Учитывая, что при попадании случайной величины X в интервал (x, x+dx) случайная величина Y с вероятностью 1 попадает в соответствующий ему интервал (y, y+dy), можно написать следующее соотношение

,

из которого вытекает

, (5.1)

где f ^-1(y) – обратная функция (x = x (y) = f ^-1(y)).

Дифференциалы dx, dy и производная обратной функции в полученном выражении взяты по модулю в силу свойства положительности плотности вероятности.

 

Примеры:

 

1. Линейное безынерционное преобразованиеy = f (x) = ax + b.

Обратная функция ,

.

Таким образом, при линейном преобразовании случайной величины ее кривая плотности распределения смещается на величину b, а масштаб по координатным осям изменяется в |a| раз.

2. Кусочно-линейное преобразование y = f (x) (рис. 5.3).

Задачу решим графически, определяя вид кривой w_Y (y) на отдельных интервалах оси у.

y y y 2 y 1 x 1 x 2 x 0 w (y) w (x)     x 1 x 2 x Рис. 5.3. Кусочно-линейное преобразование случайной величины.

Из рассмотрения функциональной характеристики y = f (x) с очевидностью вытекает, что

а) при у < 0 и у > y ₂ w_Y (y) = 0, т. к. значения реакции у не могут выйти за пределы уровней отсечки (у = 0) и насыщения (у = y ₂,);

б) при 0 < у < y ₁ w_Y (y) = 0, т. к. в этот интервал (протяженностью y ₁) значения реакции попадают при единственном значении воздействия x = x ₁, вероятность которого w_X (x ₁) dx ® 0;

в) при y ₁ ≤ у < y ₂ , где b = y ₁, (см. пример 1);

г) при у = 0 , т. к. у = 0 для всех х < x ₁;

д) при у = у ₂ , т. к. у = у ₂ для всех х > x ₂.

3. Преобразование при неоднозначной обратной функции

.

На практике встречаются ситуации, когда обратная функциональная характеристика является многозначной (рис. 5. 4). Рассуждая аналогично тому, как это делали при выводе выражения (5.1), легко убедиться в том, что в этом случае для интервала

.

Если при анализе прохождения СП через БФУ достаточно знать только основные характеристики распределения реакции, то их можно найти, не определяя w_Y (y). В частности:

математическое ожидание

,

дисперсия

функция корреляции

.

 

Функциональное преобразование двух случайных процессов

Постановка задачи:

Заданы два случайных процесса X ₁(t) и X ₂(t) с известной совместной плотностью вероятности их значений в совпадающие моменты времени w (x ₁, x _2­; t). С этими процессами связаны два других СП Y ₁(t) и Y ₂(t) известными функциональными зависимостями

.

Требуется определить w (у ₁, у _2­; t) ­­– совместную плотность вероятности процессов Y ₁(t) и Y ₂(t) в совпадающие моменты времени.

Решение:

По аналогии с (5.1) можно написать следующее соотношение

,

где J – якобиан преобразования переменных x ₁, x _2­ в у ₁, у _2­

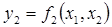. (5.2)