
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некогерентного приема в двоичной системе связиСодержание книги
Поиск на нашем сайте
Для определения средней вероятности ошибки оптимального некогерентного приема в двоичной системе при равных вероятностях передаваемых сообщениях P (b 0) = P (b 1) достаточно вычислить условную вероятность ошибки любого типа, как это было установлено в разделе 6.4,
надо знать плотности вероятности
где i – номер ветви (индекс сигнала, на который настроен СФ)
j – индекс передаваемого сообщения.
Запишем отсчеты огибающих V 0 и V 1 на выходах соответствующих ветвей демодулятора при передаче сигнала s 1(t) (j = 1) i = 0 i = 1 Входящие в эти выражения скалярные произведения
представляют собой нормально распределенные случайные величины с нулевым математическим ожиданием, следовательно, огибающие Vi будут иметь распределение Рэлея на выходе СФ0 (i = 0)
и обобщенное распределение Рэлея на выходе СФ1 (i = 1)
Вернемся к вычислению средней вероятности ошибки при оптимальном некогерентном приеме
Произведя замену переменных
получим
Обозначим 2 V 1= V, 2σ2 = g2, тогда
Здесь учтено то, что подынтегральное выражение можно трактовать как плотность вероятности обобщенного распределения Рэлея (5.13). Вычислим σ2 – мощность шума на выходе СФ
и окончательно получим
где, как и ранее, Полученный результат относится к любым двоичным системам, использующим ортогональные в усиленном смысле сигналы. Нетрудно сообразить, что для некогерентного приема в двоичных системах с пассивной паузой (АМ)
На рис. 6.39. приведены кривые помехоустойчивости оптимального некогерентного приема сигналов с АМ, ЧМ и ОФМ.
На практике используют также квазиоптимальный прием ЧМ сигналов, применяя в схеме (рис. 6.37) вместо СФ (согласованных с сигналами по их форме) полосовые фильтры (ПФ) с прямоугольной АЧХ, согласуя их с шириной спектра сигналов. В.И.Сифоровым было установлено, что максимальное отношение с/ш на выходе ПФ с прямоугольной АЧХ достигается при ширине полосы пропускания
1. Сформулируйте задачу синтеза оптимального некогерентного демодулятора. 2. Напишите алгоритм оптимального приема дискретных сообщений в канале с неопределенной фазой. 3. Как упрощается алгоритм некогерентного приема при условии равенства энергий используемых сигналов? 4. Нарисуйте схему оптимального некогерентного демодулятора для системы сигналов с разными энергиями. 5. Нарисуйте схему оптимального некогерентного демодулятора для системы сигналов с равными энергиями. 6. Как вычисляется огибающая Vi. 7. Нарисуйте схему блока определения огибающей Vi. 8. Нарисуйте схему оптимального некогерентного демодулятора на согласованных фильтрах. 9. Что означает ортогональность сигналов в усиленном смысле? 10. Почему для достижения максимальной помехоустойчивости некогерентного приема требуется использование ортогональных в усиленном смысле сигналов? 11. Приведите примеры систем ортогональных в усиленном смысле сигналов. 12. При каких видах цифровой модуляции возможен некогерентный прием сигналов? 13. Изложите методологию расчета средней вероятности ошибок при оптимальном некогерентном приеме. 14. Почему возможен некогерентный прием сигналов с ОФМ, а с ФМ – нет? 15. Приведите формулы для вычисления средней вероятности ошибочного некогерентного приема АМ, ЧМ и ОФМ сигналов. 16. Что называют квазиоптимальным некогерентным приемом? В чем его достоинства и недостатки?
Рекомендации по проведению экспериментальных
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 698; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.177.46 (0.009 с.) |

 .
. Вычислим
Вычислим  , ориентируясь на схему некогерентного демодулятора на СФ (рис. 6.37). Ошибка вида
, ориентируясь на схему некогерентного демодулятора на СФ (рис. 6.37). Ошибка вида 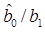 (при передаче сообщения b 1 принимается решение в пользу
(при передаче сообщения b 1 принимается решение в пользу  ) возникает, если для отсчетов огибающих на выходах ветвей демодулятора выполняется неравенство
) возникает, если для отсчетов огибающих на выходах ветвей демодулятора выполняется неравенство  . Для определения его вероятности
. Для определения его вероятности
 и
и  , вычислением которых и займемся. Вспомним, что
, вычислением которых и займемся. Вспомним, что ,
, ,
,
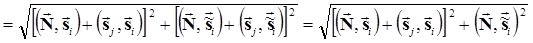 .
.
 .
.

 .
.
 .
.


 .
. и
и .
.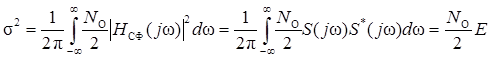
 ,
, .
.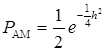 .
. Некогерентный прием сигналов с ФМ исключается, т.к. огибающие противоположных сигналов неразличимы, однако возможна реализация оптимального некогерентного демодулятора для системы с ОФМ (рис. 6.38), сигналы которой ортогональны в усиленном смысле на двойном интервале 2 Т и, следовательно, имеют на этом интервале удвоенную энергию. По этой причине
Некогерентный прием сигналов с ФМ исключается, т.к. огибающие противоположных сигналов неразличимы, однако возможна реализация оптимального некогерентного демодулятора для системы с ОФМ (рис. 6.38), сигналы которой ортогональны в усиленном смысле на двойном интервале 2 Т и, следовательно, имеют на этом интервале удвоенную энергию. По этой причине .
. и оно, естественно, несколько меньше, чем для СФ (энергетический проигрыш 0,86 дБ). Дополнительное снижение помехоустойчивости при использовании ПФ вызывается межсимвольной интерференцией, возникающей из-за наложения переходных процессов от предшествующих посылок на последующие (что не имеет места при согласованной фильтрации).
и оно, естественно, несколько меньше, чем для СФ (энергетический проигрыш 0,86 дБ). Дополнительное снижение помехоустойчивости при использовании ПФ вызывается межсимвольной интерференцией, возникающей из-за наложения переходных процессов от предшествующих посылок на последующие (что не имеет места при согласованной фильтрации). Контрольные вопросы
Контрольные вопросы


