
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисперсия абсолютно непрерывной случайной величины.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Дисперсия абсолютно непрерывной случайной величины X с функцией плотности f(x) и матема-тическим ожиданием m = M(X) определяется таким же равенством, как и для дискретной величины
Из равенства (5.26) следует, что справедлива следующая формула
Поскольку формула (5.29) может быть записана в следующем виде
то формулу (5.30) можно представить таким образом
В случае когда абсолютно непрерывная случайная величина X сосредоточена на промежутке [a, b], формулы (5.30), (5.32) примут вид
Дисперсия непрерывной случайной величины определяет степень рассеивания значений, прини-маемых случайной величиной, вокруг ее математического ожидания. Среднее квадратичное отклонение, или стандартное отклонение, непрерывной случайной ве-личины X определяется так же, как и для дискретной случайной величины:
4 °. Свойства математического ожидания и дисперсии. Для математического ожидания и дисперсии непрерывной случайной величины X сохраняются свойства числовых характеристик дискретной случайной величины. Напомним эти свойства. 4. Постоянный множитель выносится из под знака дисперсии в квадрате.
5. Если к случайной величине прибавить константу, то дисперсия не изменится.
6. Дисперсия суммы независимых случайных величин равна сумме дисперсий этих величин.
Это не полное т.к. доказать не могу=( 82. Выведите формулу для нахождения мат. ожидания и дисперсии случайной величины, равномерно распределенной на отрезке [a; b]. C.В. Х, сосредоточенная на [a;b], равномерно распределена на этом отрезке, если её функция плотности равна константе: f(х)=с (const), a≤х≤b. Значение постоянной с определяется из условия: ∫∞-∞ f(х)dх=1, которому удовлетворяет любая плотность вероятности. В данном случае это условие принимает вид: с(b-a)=1, откуда следует, что с=1/(b-a). М(Х)= ∫ba хf(х)dх= ∫ba сdх, т.к. для абсолютно непрерывной С.В. Х с непрерывной плотностью f(х) М(Х)= ∫ba хf(х)dх. Т.к. с=1/(b-a), то М(Х)=с*х2/2 |ba = c*(b2-a2)/2=(b+a)/2. Таким образом мы получили, что числу М(Х) соответствует середина [a; b]. Для нахождения дисперсии воспользуемся формулой, где D(Х)= ∫ba х2f(х)dх- m2, где m=M(Х). D(Х)= 1/(b-a) ∫ba х2dх – ((a+b)/2)2= 1/(b-a)*(b3-a3)/3 - ((a+b)/2)2= (b2+ab+a2)/3 - ((a+b)/2)2= (b-a)2/12.
Таким образом, М(Х)=(b+a)/2, а D(Х)= (b-a)2/12. 83. Объясните (с доказательством) вероятностный смысл параметра m в формуле Формула Как видно, нормальное распределение определяется двумя параметрами: m и Поопределению математического ожидания непрерывной с.в.,
Первое из слагаемых равно нулю (под знаком интеграла нечетная функция; пределы интегрирования симметричны относительно начала координат). Второе из слагаемых равно m (интеграл Пуассона Итак, M(X)=m, т.е. математическое ожидание нормального распределения равно параметру m. 84. Объясните (с доказательством) вероятностный смысл параметра σ в формуле для функции плотности Докажем, что 85. Докажите, что для случайной величины, распределенной по показательному закону с параметром Найти числовые характеристики случайной величины X, распределенной по пока-зательному закону с плотностью Решение. Для нахождения математического ожидания воспользуемся формулой M(X)= Найдем интеграл методом интегрирования по частям, полагая u = x, dv = e –λ x d (λ x), так что du = dx, v = – e –λ x . Получим Таким образом, M(X)= 86 Случайная величина X равномерно распределена на отрезке [a,b]. Можно ли для любых m и δ>0 подобрать параметры a и b так, чтобы M(x)=m, D(x)=δ2? Как по m и δ найти a и b?
СВ Х, сосред. на [a,b] называется равном. распередёлнной, если её
Если M(x)=m, а D(x)= δ2 и m, δ>0 – любые, тогда мы всегда можем подобрать параметры a и b, чтобы выполнялось это условие. Пример: пусть m=3, δ=4 – тогда
87.Что такое правило Правило трех сигм – отклонение любой случайной величины от ее математического ожидания будет не более трех средних квадратических отклонений (по абсолютной величине). Правило трех сигм применимо для большинства СВ, встречающихся на практике. P (|X-a|<=3сигма) для нормального закона = 0,9973. Для равномерного закона =1. Для показательного = 0,9827 и т.д. Для нормально распределенной с.в.Х справедлива формула Преобразуем эту формулу, приняв
Если t=3 и, следовательно,
2. Верно.
88. Формулируйте определение начальных Начальным моментом порядка k (k принадлежит N), свободная величина Х называется мат.ожиданием k-й степени Х.
Центральным моментом порядка k СВ Х называется мат.ожидание k-й степени отклонения:
Теорема: если Х и У независимые СВ, то Док-во:
89. Пусть Докажите, что: Докажем связь начальных и центральных моментов:
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 971; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.155 (0.006 с.) |





 .
. 




 для функции плотности случайной величины Х, распределенной по нормальному закону.
для функции плотности случайной величины Х, распределенной по нормальному закону. описывает плотность нормального распределения вероятностей непрерывной с.в..
описывает плотность нормального распределения вероятностей непрерывной с.в.. . Достаточно знать эти параметры, чтобы задать нормальное распределение. Докажем, что вероятностный смысл этих параметров таков: m есть математическое ожидание.
. Достаточно знать эти параметры, чтобы задать нормальное распределение. Докажем, что вероятностный смысл этих параметров таков: m есть математическое ожидание. Введем новую переменную
Введем новую переменную  . Отсюда
. Отсюда  . Приняв во внимание, что новые пределы интегрирования равны старым, получим
. Приняв во внимание, что новые пределы интегрирования равны старым, получим
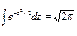 ).
). случайной величины, распределенной по нормальному закону.
случайной величины, распределенной по нормальному закону. - среднее квадратическое отклонение нормального распределения.
- среднее квадратическое отклонение нормального распределения.  Введем новую переменную z==(х—m)/
Введем новую переменную z==(х—m)/  . Отсюда
. Отсюда  . Приняв во внимание, что новые пределы интегрирования равны старым, получим
. Приняв во внимание, что новые пределы интегрирования равны старым, получим  Интегрируя по частям, положив u=z,
Интегрируя по частям, положив u=z,  найдем
найдем  Следовательно,
Следовательно,  .Итак, среднее квадратическое отклонение нормального распределения равно параметру
.Итак, среднее квадратическое отклонение нормального распределения равно параметру 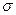 .
.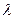 , математическое ожидание
, математическое ожидание 




 на [a,b].
на [a,b].
 докажем это
докажем это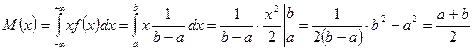



 ;
; 

 ;
;  ;
;  ;
; 
 для нормального распределения? Верно ли, что для любой нормальной случайной величины Х существует отрезок
для нормального распределения? Верно ли, что для любой нормальной случайной величины Х существует отрезок  , для которого
, для которого  ? Ответ обоснуйте.
? Ответ обоснуйте.
 В итоге получим
В итоге получим
 , то
, то  , т.е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.
, т.е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973. моментов случайной величины. Докажите, что если Х и У независимые случайные величины, то
моментов случайной величины. Докажите, что если Х и У независимые случайные величины, то 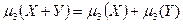






 - начальные, а
- начальные, а  - центральные моменты некоторой случайной величины.
- центральные моменты некоторой случайной величины.




