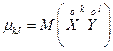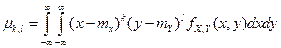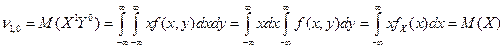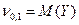Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сформулируйте определение асимметрии As(X ) случайной величины X и укажите ее основные свойства. Что характеризует асимметрия случайной величины?Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Асимметрией распределения называют отношение третьего центрального момента к кубу стандартного отклонения:
Замечание. Асимметрия случайной величины X совпадает с третьим начальным (центральным) моментом соот-ветствующей нормированной случайной величины. Действительно, по определению
Свойство 1. Асимметрия и эксцесс инвариантны относительно линейной замены случайной ве-личины:
Таким образом, асимметрия и эксцесс не меняются при сдвигах и растяжениях и их можно ис-пользовать в качестве характеристик формы распределения. Свойство 2. Для независимых случайных величин X1, …, Xn имеем
Заметим, что в случае одинаково распределенных независимых случайных величин X1, …, Xn асимметрия и эксцесс их суммы стремится к нулю, когда n →
Сформулируйте определение эксцесса Ex(X) случайной величины X и укажите его основные свойства. Чему равен эксцесс для нормального распределения? Эксцессом распределения назыв. величина:
для норм. распределения Ex=0 (поскольку для станд. норм. распред. N(0,1) Св-ва: 1 2
i=1,…,n
В случае одинаково распред. нез. сл. вел
92 Найдите асимметрию и эксцесс равномерного распределения на отрезке [а,b]. Тк As и Ex не меняются при меняющихся заменах, а любое равномерное распределение на отрезке может быть получено линейной заменой из любого другого равномерного распределения, например, из равномерного распределения на отрезке, то достаточно посчитать As и Ex для этого распределения.
Плотность fx=1/(b-a)=1, μ3= Sb a fx(t)tdt== Sb a tdt=t2/2 в пределах от a до =(b-a)2/2 D== Sb a fx(t)t2dt=(b-a)3/3 σ=√D=√(b-a)3/3 As=μ3/σ3=((b-a)2/2)/(√(b-a)3/3)
μ4= M[(x-M(x)4] fx(t)tdt= Sb a t4dt=(b-a)5 /5 Что называется системой случайных величин? Сформулируйте определение функции распределения двумерного случайного вектора (Х,Y) и дайте его геометрическую интерпретацию. Определение. Упорядоченная пара случайных величин (X, Y), определенных на одном и том же пространстве элементарных событий Ω, называется системой случайных величин, двумерным случайным вектором или двумерной случайной величиной. Определение. Функцией распределения двумерной случайной величины (X, Y) называется ве-роятность совместного выполнения двух событий X < x и Y < y
Геометрической интерпретацией может служить рис, на котором значением функции распределения может служить вероятность попадания случайной величины (X, Y) в бесконечный квад-рант Q (x, y) с вершиной в точке (x, y), лежащий левее и ниже ее.
94. Сформулируйте основные свойства функции распределения случайного вектора (Х,У) и приведите примеры двумерной функции распределения. 1) 0 ≤ F(x) ≤ 1 вытекает из вероятностного смысла функции распределения . 2) F(x)- неубывающая функция, т.е. Следствие 1. Вероятность того, что непрерывная случайная величина X примет одно определённое значение, равна нулю, т.е. Р(Х=х1)=0. =F(b)-F(a)/ Следствие 2. Вероятность того, что непрерывная случайная величина X примет одно определённое значение, равна нулю, т.е. Р(Х=х1)=0. 3) Если возможные значения случайной величины принадлежат интервалу (a;b), то 1) F(x)=0, х ≤ a, 2) F(x)=1, х ≥ b. Следствие: Если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливо равенство: Свойства функции совместного распределения Для простоты обозначений все дальнейшие рассуждения и формулировки приводятся в случае n=2 для случайного вектора 1) 2) 3) Для любого i =1,2существует 4) Функция
Функция, дающая для любой пары значений x, y вероятность того, что случайная величина Х будет меньше или равна x, а случайная величина Y меньше или равна y: Лапласа-Гаусса
95. Какой случайный вектор называется абсолютно непрерывным? Укажите основные свойства функции плотности распределения двумерного случайного вектора. Как можно найти непрерывную функцию плотности распределения двумерного случайного вектора, если известна его функция распределения? Укажите функцию плотности для равномерного распределения в круге радиуса R. Случайный вектор называется абсолютно непрерывным, если существует
Свойства f(x;y): 1) f(x;y) – неотрицательная 2) 3) Если F(х;у) известна => Пример: Случ вектор (Х;У) равномерно распределен в круге радиуса R. Найти функцию плотности.
96. Как найти функцию распределения Ответ: По св-ву плотности распределения следует:
Равномерное распределение в прямоугольнике => F(x,y)=
1 =
F(x,y)= F(x,y)= = =
97. Как найти функцию плотности fx(x) и fy(y) компонент Х и Y, если известна функция плотности fX,Y(x,y) двумерного распределения (Х,Y)? Для того чтобы найти функцию распределения компоненты при известной функции распределения двумерного распределения. Необходимо проинтегрировать данную функцию распределения по противоположной компоненте, т.е. fx(x)=
f(x,y)=
fx(x)=
98. Как можно найти функцию (,), f x y X Y плотности распределения случайного вектора (X, Y) с независимыми компонентами X и Y, если известны их плотности распределения f (x) X и f (y) Y? Будут ли независимыми компоненты случайного вектора (X, Y), равномерно распределенного в прямо- угольнике a ≤ x ≤ b, c ≤ y ≤ d? Ответ обоснуйте. По определению: Компоненты Х и У абсолютно непрерывного случайного вектора называются независимыми, если
Пример: прямоугольник F(x;y)= При решении уравнения
а) б)
Аналогично для
Компоненты Х и У - независимые 99. Как можно найти функцию распр Fx,y(x,y) случайного вектора (X,Y) с независимыми компонентами X и Y, если известны их ф-ии распр FX(x) и FY(y)? Если X и Y – независимые компоненты случ вектора (X,Y) и известна их ф-ия распр FX(x) и FY(y), то его ф-ия распр Fx,y(x,y)= FX(x)*FY(y). Обоснование. Пусть A=(X<x), B=(Y<y), тогда P((XÎA)(YÎB))=Fx,y(x,y) и P(XÎA)*P(YÎB)=FX(x)*FY(y), т.к. P((XÎA)(YÎB))=P(XÎA)*P(YÎB) (т.к. X и Y –независимые). 100. Как найти математическое ожидание функции Для математического ожидания функции ф(х, у) от компонент случайного вектора (X, Y) справедлива формула
Мы видели, что в одномерном случае основные числовые характеристики случайной величины выражались через начальные и центральные моменты. Дадим аналогичное определение для случайного вектора.
Началъным моментом порядка (к, 1} называется математическое ожидание функции хку':
Центральным моментом порядка (к, Г) называется математическое ожидание функции (х-тх) \y-mY),где тх = М(Х), mY = M{Y):
Числа к и l характеризуют порядок момента по отношению к каждой компоненте случайного вектора. Число r = к + l называют суммарным порядком момента. Соответственно суммарному порядку моменты можно разделить на моменты первого, второго и т.д. порядка. Мы рассмотрим более подробно моменты первого и второго порядка. Первые начальные моменты - это нам уже знакомые математические ожидания случайных величин X и Y.
Аналогично, Точка с координатами (М(Х), M(Y)) характеризует центр системы случайных величин, вокруг которого происходит рассеивание возможных значений. Кроме первых моментов широко применяют вторые центральные моменты, которые бывают трех типов. Два из них дают знакомые нам дисперсии компонент X и Y:
которые характеризуют рассеивание возможных значений случайных величин X и 7 вдоль осей х и у. Особую роль в определении взаимодействия компонент играет второй смешанный центральный момент
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 424; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.214.185 (0.009 с.) |





 ,
, 
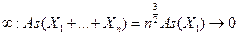

 )
)


 им. один дисперсию, то
им. один дисперсию, то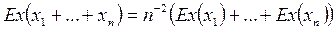

 As=μ3/σ3, σ=√D, μ3=M[(x-M(x)3]
As=μ3/σ3, σ=√D, μ3=M[(x-M(x)3] Ex= μ4/σ4-3
Ex= μ4/σ4-3 Ex= μ4/σ4-3=((b-a)5 /5)/((b-a)3/3)2 - 3
Ex= μ4/σ4-3=((b-a)5 /5)/((b-a)3/3)2 - 3


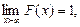

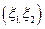
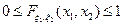
 не убывает по каждой координате вектора
не убывает по каждой координате вектора  .
.


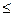 x; Y
x; Y 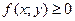 - плотность распределения, такая, что:
- плотность распределения, такая, что:
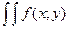 dxdy=1
dxdy=1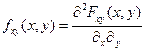 В точке непрерывности
В точке непрерывности 
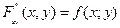 - в точках непрерывности f(x,y).
- в точках непрерывности f(x,y). кругу (if = если)
кругу (if = если)
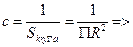
 кругу
кругу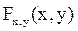 двумерного случайного вектора (X,Y), если известна функция плотности распределения f
двумерного случайного вектора (X,Y), если известна функция плотности распределения f  ? Укажите функцию распределения
? Укажите функцию распределения 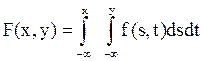
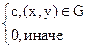
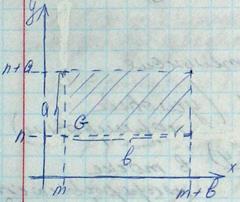

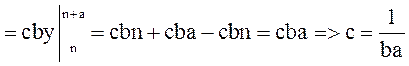

 т.к. иначе F(x,y), x>m+b, y>n+a, F(x,y)=1, x<m, y<n F(x,y=0]=
т.к. иначе F(x,y), x>m+b, y>n+a, F(x,y)=1, x<m, y<n F(x,y=0]=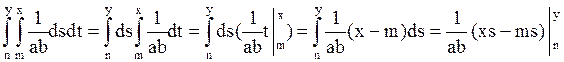 =
=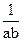 (x(y-n)-m(y-n))=
(x(y-n)-m(y-n))= 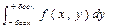 и соответственно наоборот.
и соответственно наоборот.

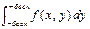 = 1/36
= 1/36 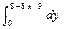 =
= 
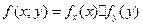
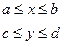 , в котором вектор (х,у) равномерно распределен.
, в котором вектор (х,у) равномерно распределен. иначе
иначе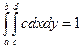 найдем
найдем 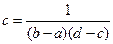
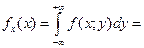
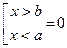
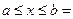
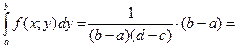
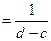
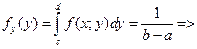
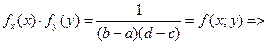
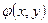 , где Х,У – компоненты случайного вектора (Х,У)? Как определяются начальные
, где Х,У – компоненты случайного вектора (Х,У)? Как определяются начальные  k,l и центральные
k,l и центральные 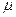 k,l моменты случайного вектора (Х,У)?
k,l моменты случайного вектора (Х,У)?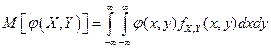

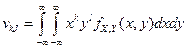
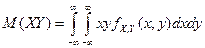 (1)
(1)