
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выбирается в круге радиуса r? в кубе со стороной a?Содержание книги
Поиск на нашем сайте
Геометрический подход заключается на предположении, что попадание каждой точки в геометрическом множестве( 1) F – фигура
P(F)=площадь F/площадь круга радиуса r
2) P(F)=объем F/ объем круга 25. Что такое полная группа событий? Приведите пример, когда события АВ, Полная группа событий - это система случайных событий такая, что в результате произведённого случайного эксперимента непременно произойдёт одно из них. АВ, А*В, А*+В* (чёрточка одна на А и В)-не образуют полной группы событий. А*+В*(чёрточка одна на А и В)=А*В* Полную группу событий составляют: АВ, А*В, АВ*, А*В* Сл-но АВ, А*В, А*В* - не образуют полной группы. Пример: студент сдаёт 2 зачёта, соб.А- сдан 1 зачёт, соб.В- сдан 2 зачёт, Р(А)=1/2, Р(В)=2/3 Р(АВ+А*В+А*В*)≠1, т.к. Р(АВ*)≠0, сл-но соб. АВ, А*В, А*+В* (чёрточка одна на А и В)-не образуют полной группы. 26. Верно ли, что события Да, события
27 Если в каждом из n независимых испытаний вероятность р появления A const, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абс величине будет сколь угодно малым, если число испытаний достаточно велико. xi- попарно независ., тогда D(xi)=pq. Т.к. p+q=1, то pq Применим т. Чебышева, получим Матем ожидание а каждой из величин xi = р наступл. событ. Каждая xi при появлении события в соотв. испытании принимает значение = единице Учитывая это, получим, 28. Сформулируйте и докажите формулу полной вероятности. Приведите пример ее применения. Пусть событие А может наступить при условии появления одного из несовместных событий В1, В2,В3,…., Вn, которые образуют полную группу. Пусть известны вероятности этих событий и условные вероятности Р в2 (А), …., Рвn (А) события А. Найдем вероятность события А.
Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий В1, В2,…,Вn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А: Р(А) = Р(В1) Рв1(А) + Р(В2) Рв2(А) +….+ Р(Вn) Рвn(А).
Эта формула называется «формулой полной вероятности». Докажем ее… По условию, событие А может наступить, если наступит одно из несовместных событий В1,В2,…,Вn. Другими словами, появление события А означает осуществление одного, безразлично какого, из несовместных событий В1А, В2А,…, ВnА. Пользуясь для вычисления события А теоремой сложения, получаем Р(А) = Р(В1А) + Р(В2А) +….+ Р(ВnА) (1) Остается вычислить каждое из слагаемых. По теореме умножения вероятностей зависимых событий имеем: Р(В1А) = Р(В1) Рв1(А); Р(В2) Рв2(А): …. Р(ВnА) = Р(Вn) Р(bn) (А) Подставляем правые части этих равенств в соотношение (1) и получаем формулу полной вероятности: Р(А) = Р(В1) Рв1(А) + Р(В2)Рв2 (А) + ….+ Р(Вn) Рвn (А) Приведем пример использования формулы полной вероятности: Допустим, у нас есть два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго – 0,9. Найдем вероятность того, что взятая наудачу деталь (из наудачу взятого набора) – стандартная. Пусть А событие «извлеченная деталь стандартна». Деталь может быть извлечена либо из первого набора (событие В1), либо из второго (В2). Вероятность того, что деталь вынута из первого набора, Р(В1) =1/2, вероятность, что деталь вынута из второго набора, Р(В2) = 1/ 2. Условная вероятность того, что из первого набора будет извлечена стандартная деталь, Рв1 (А) =0,8, условная вероятность того, что из второго набора будет извлечена стандартная деталь Рв2(А) =0,9. Искомая вероятность того, что извлеченная наудачу деталь – стандартная, по формуле полной вероятности равна Р(А) = Р(В1) Рв1(А) + Р(В2)Рв2 (А) = 0,5*0,8 + 0,5*0,9 = 0,85.
29. Сформулируйте и докажите формулу Байеса. Приведите пример ее применения. Пусть событие А может наступить при условии появления одного из несовместных событий В1,В2,…,Вn, образующих полную группу. Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности:
Р(А) = Р(В1) Рв1(А) + Р(В2)Рв2 (А) + ….+ Р(Вn) Рвn (А) (1) Допустим, что произведено испытание, в результате которого появилось событие А. Определим, как изменились, в связи с тем, что событие А уже наступило, вероятности гипотез. Другими словами, будем искать условные вероятности Ра(В1), Ра(В2),…., Ра(Вn). Найдем вначале условную вероятность Ра(В1). По теореме умножения имеем Р(АВ1) = Р(А) Ра(В1) = Р(В1)Рв1(А) Отсюда Ра(В1) = Р(В1)Рв1(А) Р(А) Заменим здесь Р(А) по формуле (1), получаем pA(Hi)= рвi(A)p(Вi). рВ1(А1)р(В1)+рВ2(А)р(В2)+…+рВn(А)р(Вn) Аналогично выводятся формулы, определяющие условные вероятности остальных гипотез, т.е. условная вероятность любой гипотезы Вi (i= 1,2,…,n) может быть вычислена по формуле Ра(Вi) = Р(Вi) Рвi(А) Р(В1) Рв1(А) + Р(В2) Рв2(А)+….+Р(Вn) Рвn(А) Полученные формулы называются формулы Байеса. Они позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А. Пример: Имеется три одинаковых по виду ящика. В первом ящике n=12 белых шаров, во втором – m=4 белых и n-m=8 черных шаров, в третьем – n=12 черных шаров. Из выбранного наугад ящика вынули белый шар. Найдите вероятность Р того, что шар вынут из второго ящика. Решение.
30. В чем состоит схема Бернулли? Запишите формулу Схема Бернулли: производится n независимых испытаний, в каждом из которых с одной и той же вероятностью p наступает некоторое событие А (называемое обычно «успехом») и, следовательно, с вероятностью q=1-p наступает событие Пусть k – любое из чисел 0,1,2,…, n. Обозначим
Пример: Монета бросается 10 раз. Какова вероятность того, что герб выпадает при этом ровно 3 раза? Решение: В данном случае успехом считается выпадение герба, вероятность p этого события в каждом опыте равна ½, так что q=1-p=1|2. Отсюда
31. Выведите формулу Когда производится n одинаковых и независимых опытов, каждый из которых имеет только 2 исхода { A; Пространство элементарных событий каждой серии испытаний содержит Для большей наглядности условимся каждое наступление события А рассматривать как успех, ненаступление А – как неуспех. Наша цель – найти вероятность того, что из n опытов ровно k окажутся успешными; обозначим это событие временно через B. Событие В представляется в виде суммы ряда событий – вариантов события В. Чтобы фиксировать определенный вариант, нужно указать номера тех опытов, которые оканчиваются успехом. Например, один из возможных вариантов есть
|
|||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 374; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.251.22 (0.011 с.) |

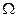 ), а в какое-то подмножество А
), а в какое-то подмножество А 
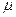 (А), где
(А), где 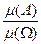 .
. и
и 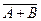 не образуют полной группы событий.
не образуют полной группы событий. образуют полную группу для любых событий А и В? Ответ обоснуйте.
образуют полную группу для любых событий А и В? Ответ обоснуйте.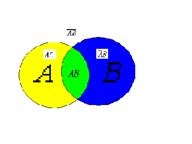
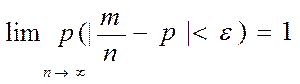 xi-число появлений событий в i-м испытании (i=1…n). Каждая из величин может принимать 2 значения: 1 с вер-ю р, 0 с вер q
xi-число появлений событий в i-м испытании (i=1…n). Каждая из величин может принимать 2 значения: 1 с вер-ю р, 0 с вер q 1/4
1/4  дисперсии огранич с=1/4
дисперсии огранич с=1/4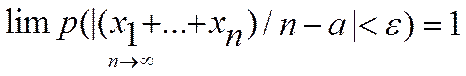
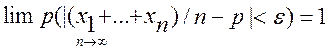
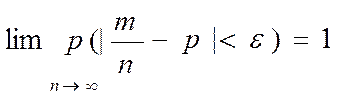
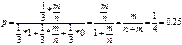
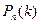 для вероятности k успехов в серии n испытаний по схеме Бернулли и приведите пример ее применения.
для вероятности k успехов в серии n испытаний по схеме Бернулли и приведите пример ее применения.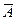 , противоположное А.
, противоположное А. вероятность того, что в n испытаниях Бернулли успехов наступит k раз. Справедлива формула Бернулли:
вероятность того, что в n испытаниях Бернулли успехов наступит k раз. Справедлива формула Бернулли: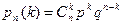 .
.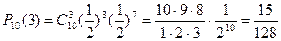 .
.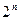 точек или последовательностей из символов А и
точек или последовательностей из символов А и 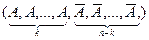 . Число всех вариантов равно, очевидно,
. Число всех вариантов равно, очевидно,  , а вероятность каждого варианта ввиду независимости опытов равна
, а вероятность каждого варианта ввиду независимости опытов равна 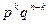 . Отсюда вероятность события В равна
. Отсюда вероятность события В равна 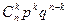 . Чтобы подчеркнуть зависимость полученного выражения от n и k, обозначим его
. Чтобы подчеркнуть зависимость полученного выражения от n и k, обозначим его 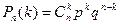 .
.


