
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Как вводятся основные характеристики статистической совокупности (выборки): среднее, дисперсия, центральные моменты высших порядков,Содержание книги
Поиск на нашем сайте
асимметрия, эксцесс? Какие из перечисленных характеристик остаются неизменными при линейных преобразованиях x → ax + b? Определение. Центральным моментом порядка k (k е N) случайной величины X называют математическое ожидание k-й степени отклонения
Для дискретных случайных величин формула для центрального момента порядка k выглядит следующим образом:
для непрерывных случайных величин
Определение. Асимметрией распределения называют отношение третьего центрального момента к кубу стандартного отклонения:
Замечание. Асимметрия случайной величины X совпадает с третьим начальным (центральным) моментом соответствующей нормированной случайной величины. Действительно, по определению
Определение. Эксцессом распределения называется величина
Поскольку для стандартного нормального распределения N(0, 1) мы нашли, что μ4 = 3 (см. (6.22)), то для нормального распределения эксцесс равен нулю. В частности, вычисляя эксцесс неизвестного распределения, мы можем судить о близости его к нор-мальному по этой числовой характеристике. Для биномиального закона
Действительно, воспользуемся формулой (6.18). Имеем
дится ниже и носит название дисперсии. Определение. Дисперсией случайной величины X называется число
Другими словами, дисперсия есть математическое ожидание квадрата отклонения. Из определения (4.8) легко вытекают следующие свойства дисперсии. остаются неизменными при линейных преобразованиях x → ax + b Дисперсия, асимметрия, эксцесс Проблемя, найдите определение средней!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! Сформулируйте определение выборочной (эмпирической) функции распр для СВ Х. Как связаны ф-ии распределения признака в генеральной и выборочной совокупностях?
Случ выборкой объема n из ген совокупности X называется случ вектор Zn=(X1…Xn), компоненты которого являются независимыми СВ, распредел так же как и X. Реализацией выборки называется вектор Zn=(X1,…Xn), его компоненты xn – реализацией Xk. Мн-во S всех реализаций выборки Zn называется выборочным пространством. F(x) – ген закон распр, то " e>0 limP(|Fn(X)-F(X)|< e)=1;
Каким образом на рисунках изображаются выборочные распределения непрерывных и целочисленных случайных величин? Что такое полигон частот? Как строится гистограмма относительных частот? Чему равна сумма площадей столбиков диаграммы? Хз как ответить на первый вопрос(в учебниках нет), наверное при помощи полигона и гистограммы. Полигоном частот называют ломаную, отрезки которой соединяют точки (х1; п1), (х2; п2),..., (xk; nk). Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат — соответствующие им частоты ni. Точки (хi; пi) соединяют отрезками прямых и получают полигон частот. Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению Wi/h (плотность относительной частоты). Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии W{/h. Площадь i-го частичного прямоугольника равна hWi/h=Wi—относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице
118.Сформулируйте понятие несмещенной точечной оценки. Будет ли оценка математического ожидания m, построенная по результатам двух измерений X1и X2 в форме m=1/10X1+(1-1/10)X2, несмещенной оценкой m?Ответ обоснуйте. Несмещенной точечной оценкой называют оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки.
119.Сформулируйте понятие несмещенной, состоятельной и эффективной оценки параметра генерального распределения. Приведите примеры. Предположим, что функция распределения генеральной совокупности имеет вид
Выборочное среднее
является состоятельной и несмещенной оценкой для генерального среднего. Выборочная дисперсия
является состоятельной, но смещенной оценкой дисперсии. Статистическая оценка
называемая исправленной дисперсией, является состоятельной несмещенной оценкой генеральной дисперсии. 120.Докажите, что для генерального распределения с математическим ожиданием m и конечной дисперсией σ2 выборочное среднее является несмещенной и состоятельной оценкой m. Выборочное среднее ¯ x=1/n*Σxn является несмещённой состоятельной оценкой математического ожидания m. Док-во. Поскольку каждая из величин генеральной выборки имеет математическое ожидание M(X), математическое ожидание выборочного среднего ¯ M(X)= 1/n*Σ M(Xi) = M(X), т.е выборочное среднее является несмещённой оценкой. В силу независимости величин выборки D ¯ x=1/n2*ΣD(Xi)=D(x)/n. Состоятельность докажем с помощью нер-ва Чебышева для выборочного среднего с учётом несмещённости: ρ(׀ ¯ x - M(X)׀>= ε) <= D(¯ x) / ε2 = D(x)/n ε2 для всякого ε>0. Поэтому limn→∞ ρ(׀ ¯ x - M(X)׀>= ε)=0. Отсюда limn→∞ ρ(׀ ¯ x - M(X)׀< ε)= 1 - limn→∞ ρ(׀ ¯ x - M(X)׀>= ε) = 1.
121. Пусть X1,…Xn – выборка из распр с дисперсией s2. Док-те, что Пусть Zn = (x1…xn) – случ выборка объема n, тогда исправленной выборочной дисперсией называется величина s2=n/(n-1) M(S2)=M(n/(n-1) M(
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 354; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.83.104 (0.009 с.) |

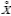 = X – m, где m – математическое ожидание X:
= X – m, где m – математическое ожидание X: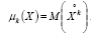



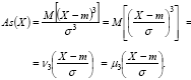
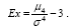
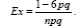
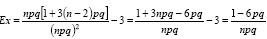
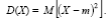
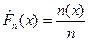 , где n(x)=
, где n(x)= 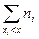 - эмпирическая ф-ия распределения. Она обладает всеми свойствами функции распределения, при этом она кусочно-постоянна.
- эмпирическая ф-ия распределения. Она обладает всеми свойствами функции распределения, при этом она кусочно-постоянна.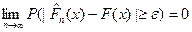 ;
; 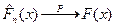 при n →µ.
при n →µ.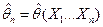 параметра
параметра 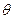 называется несмещенной, если
называется несмещенной, если 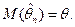 В противном случае оценка – смещенная.
В противном случае оценка – смещенная. 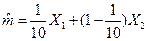 - является ли несмещенной оценкой?
- является ли несмещенной оценкой?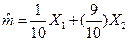
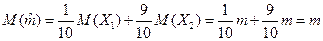
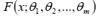 где
где 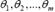 неизвестные параметры. Функцию
неизвестные параметры. Функцию  , которая при фиксированных значениях
, которая при фиксированных значениях 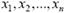 принимает значение, рассматриваемое как приближенное зна-чение неизвестного параметра θ генерального распределения, называют статистической оценкой па-раметра θ. По определению оценка является несмещенной, если ее математическое ожидание равно оцениваемому параметру. Эффективной называют оценку, которая при заданном объеме выборки п
принимает значение, рассматриваемое как приближенное зна-чение неизвестного параметра θ генерального распределения, называют статистической оценкой па-раметра θ. По определению оценка является несмещенной, если ее математическое ожидание равно оцениваемому параметру. Эффективной называют оценку, которая при заданном объеме выборки п  имеет наименьшую возможную дисперсию. Наконец, оценка называется состоятельной, если при она стремится (по вероятности) к оцениваемому параметру.
имеет наименьшую возможную дисперсию. Наконец, оценка называется состоятельной, если при она стремится (по вероятности) к оцениваемому параметру.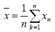
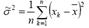

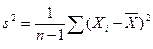 - несмещенная оценка s2.
- несмещенная оценка s2.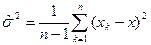 . Следствие: S2 – несмещенная оценка s2.
. Следствие: S2 – несмещенная оценка s2.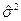 ) = n/(n-1) M(
) = n/(n-1) M(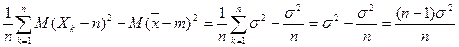 .
.


