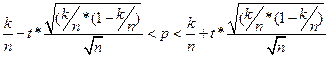Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Какие события называются достоверными и невозможными и каковы их ве-Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Какие события называются достоверными и невозможными и каковы их ве- роятности? Пусть A, B и C – случайные события. Перечислите все случаи наступления события Событие А, которое произойдет при любом испытании, называется достоверным (А = Событие А, которое не может произойти при испытании, называется невозможным (А=пуст.множ.). Например, событие А, задаваемое условием “при подбрасывании игральной кости выпало 7 очков”, является невозможным. Вероятность невозможного события равна 0. Таблица, характеризующая событие А
5.В каком случае событие В называют следствием события А? Какие события называются равными? Объясните, почему Событие А влечет за собой событие В или событие В является следствием события А (А I) А Если А наступило(А=1), то: 1) если В при этом наступило, то наступило АВ II) АВ+А Если АВ+А Событие А наступает, т.к. любое событие А попадает в В или
6. Пусть А и В – случайные события. Упростите выражение (А+В)(А+
7. Докажите, что
А
8. Докажите, что
А
9. Сформулируйте статистическое определение вероятности. Почему вероятность удовлетворяет условию Вероятность случайного события есть положительное число, заключенное между нулем и единицей. Случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0<m<n, значит, 0<m/n<1, следовательно, 0<P(A)<1. Вероятность любого события удовлетворяет двойному неравенству 0≤Р(А)≤1. В качестве статистической вероятности события понимают относительную частоту или число, близкое к ней. Свойства вероятностей вытекают из классического определения и сохраняются для статистического. А – случ.событие N – кол-во опытов, N Р(А)= А- выпала игральная кость, числа которой > 7, P(A)=0 В- выпала игральная кость, числа которой < 7, P(A)=1 Какие события называются независимыми? Докажите, что если события A и B независимы, то независимы события A и B Если выполняется равенство РB(А)=Р(А) то события А и В независимы. Для двух независимых событий А и В имеем Р(АВ)=Р(А)*Р(В)- правило умножения вероятностей для двух событий. А=АВ+АВ Þ Р(А)= Р(АВ)+Р(АВ), или Р(А)=Р(АВ)+Р(А)Р(В). Отсюда Р(АВ)=Р(А)[1-Р(В)], или Р(АВ)=Р(А)Р(В)
16. Что такое правило умножения вероятностей: а) для независимых событий Как определяется независимость в случае трех событий? Рассмотрите при- Мер: пусть в опыте с бросанием двух монет события A, В, С означают: А – на первой монете выпал герб; B – на второй монете выпал герб; C – обе монеты Ходится вероятность попадания в заданное множество, если точка случайно Может ли график функции распределения быть прямой линией? Ответ обоснуйте. Нет, не может, т.к.
44. Что такое дискретная случайная величина? Может ли таблица
Какое распределение называется абсолютно непрерывным? Что такое плотность распределения и какова ее связь с функцией распределения? Может ли абсолютно непрерывная случайная величина иметь разрывную функцию плотности f (x)? Ответ обоснуйте. Случайная величина X называется абсолютно непрерывной, если найдется неотрицательная функция f(x), называемая плотностью распределения, такая, что для a < b вероятность попадания X в промежуток [a, b] получается путем интегрирования данной функции
Для функции распределения F(x) имеем
Плотность распределения обладает следующими свойствами: 1. 2. 3.
Математическое ожидание непрерывной функции
Произвольная случайная величина X называется сосредоточенной на промежутке [a, b], если вероятность попадания X в данный промежуток равна 1. Плотность распределения абсолютно непрерывной случайной величины, сосредоточенной на промежутке [a, b], равна 0 вне [a, b]. Функцию распределения F(x) абсолютно непрерывной случайной величины, сосредоточенной на промежутке [a, b], можно представить в виде
Как вычисляется математическое ожидание в случае распределения с плотностью f(x)? Может ли для какой-либо абсолютно непрерывной случайной величины не существовать математического ожидания? Ответ обоснуйте. Математическое ожидание абсолютно непрерывной СВ Х с функцией плотности f(x) определяется равенством: М(Х)= интеграл xf(x)dx от минус беск до плюс беск Мат. ожиданием случайной величины Е называется число Если дискретная случайная величина Х принимает счетное множество возможных значений, то 81. Как вычисляется дисперсия в случае распределения с плотностью f (x)? Докажите, что для случайной величины X с плотностью Лапласа-Гаусса
95. Какой случайный вектор называется абсолютно непрерывным? Укажите основные свойства функции плотности распределения двумерного случайного вектора. Как можно найти непрерывную функцию плотности распределения двумерного случайного вектора, если известна его функция распределения? Укажите функцию плотности для равномерного распределения в круге радиуса R. Случайный вектор называется абсолютно непрерывным, если существует
Свойства f(x;y): 1) f(x;y) – неотрицательная 2) 3) Если F(х;у) известна => Пример: Случ вектор (Х;У) равномерно распределен в круге радиуса R. Найти функцию плотности.
96. Как найти функцию распределения Ответ: По св-ву плотности распределения следует:
Равномерное распределение в прямоугольнике => F(x,y)=
1 =
F(x,y)= F(x,y)= = =
97. Как найти функцию плотности fx(x) и fy(y) компонент Х и Y, если известна функция плотности fX,Y(x,y) двумерного распределения (Х,Y)? Для того чтобы найти функцию распределения компоненты при известной функции распределения двумерного распределения. Необходимо проинтегрировать данную функцию распределения по противоположной компоненте, т.е. fx(x)=
f(x,y)=
fx(x)=
98. Как можно найти функцию (,), f x y X Y плотности распределения случайного вектора (X, Y) с независимыми компонентами X и Y, если известны их плотности распределения f (x) X и f (y) Y? Будут ли независимыми компоненты случайного вектора (X, Y), равномерно распределенного в прямо- угольнике a ≤ x ≤ b, c ≤ y ≤ d? Ответ обоснуйте. По определению: Компоненты Х и У абсолютно непрерывного случайного вектора называются независимыми, если
Пример: прямоугольник F(x;y)= При решении уравнения
а) б)
Аналогично для
Компоненты Х и У - независимые 99. Как можно найти функцию распр Fx,y(x,y) случайного вектора (X,Y) с независимыми компонентами X и Y, если известны их ф-ии распр FX(x) и FY(y)? Если X и Y – независимые компоненты случ вектора (X,Y) и известна их ф-ия распр FX(x) и FY(y), то его ф-ия распр Fx,y(x,y)= FX(x)*FY(y). Обоснование. Пусть A=(X<x), B=(Y<y), тогда P((XÎA)(YÎB))=Fx,y(x,y) и P(XÎA)*P(YÎB)=FX(x)*FY(y), т.к. P((XÎA)(YÎB))=P(XÎA)*P(YÎB) (т.к. X и Y –независимые). 100. Как найти математическое ожидание функции Для математического ожидания функции ф(х, у) от компонент случайного вектора (X, Y) справедлива формула
Мы видели, что в одномерном случае основные числовые характеристики случайной величины выражались через начальные и центральные моменты. Дадим аналогичное определение для случайного вектора.
Началъным моментом порядка (к, 1} называется математическое ожидание функции хку':
Центральным моментом порядка (к, Г) называется математическое ожидание функции (х-тх) \y-mY),где тх = М(Х), mY = M{Y):
Числа к и l характеризуют порядок момента по отношению к каждой компоненте случайного вектора. Число r = к + l называют суммарным порядком момента. Соответственно суммарному порядку моменты можно разделить на моменты первого, второго и т.д. порядка. Мы рассмотрим более подробно моменты первого и второго порядка. Первые начальные моменты - это нам уже знакомые математические ожидания случайных величин X и Y.
Аналогично, Точка с координатами (М(Х), M(Y)) характеризует центр системы случайных величин, вокруг которого происходит рассеивание возможных значений. Кроме первых моментов широко применяют вторые центральные моменты, которые бывают трех типов. Два из них дают знакомые нам дисперсии компонент X и Y:
которые характеризуют рассеивание возможных значений случайных величин X и 7 вдоль осей х и у. Особую роль в определении взаимодействия компонент играет второй смешанный центральный момент
Каким образом на рисунках изображаются выборочные распределения непрерывных и целочисленных случайных величин? Что такое полигон частот? Как строится гистограмма относительных частот? Чему равна сумма площадей столбиков диаграммы? Хз как ответить на первый вопрос(в учебниках нет), наверное при помощи полигона и гистограммы. Полигоном частот называют ломаную, отрезки которой соединяют точки (х1; п1), (х2; п2),..., (xk; nk). Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат — соответствующие им частоты ni. Точки (хi; пi) соединяют отрезками прямых и получают полигон частот. Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению Wi/h (плотность относительной частоты). Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии W{/h. Площадь i-го частичного прямоугольника равна hWi/h=Wi—относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице
118.Сформулируйте понятие несмещенной точечной оценки. Будет ли оценка математического ожидания m, построенная по результатам двух измерений X1и X2 в форме m=1/10X1+(1-1/10)X2, несмещенной оценкой m?Ответ обоснуйте. Несмещенной точечной оценкой называют оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки.
119.Сформулируйте понятие несмещенной, состоятельной и эффективной оценки параметра генерального распределения. Приведите примеры. Предположим, что функция распределения генеральной совокупности имеет вид Выборочное среднее
является состоятельной и несмещенной оценкой для генерального среднего. Выборочная дисперсия
является состоятельной, но смещенной оценкой дисперсии. Статистическая оценка
называемая исправленной дисперсией, является состоятельной несмещенной оценкой генеральной дисперсии. 120.Докажите, что для генерального распределения с математическим ожиданием m и конечной дисперсией σ2 выборочное среднее является несмещенной и состоятельной оценкой m. Выборочное среднее ¯ x=1/n*Σxn является несмещённой состоятельной оценкой математического ожидания m. Док-во. Поскольку каждая из величин генеральной выборки имеет математическое ожидание M(X), математическое ожидание выборочного среднего ¯ M(X)= 1/n*Σ M(Xi) = M(X), т.е выборочное среднее является несмещённой оценкой. В силу независимости величин выборки D ¯ x=1/n2*ΣD(Xi)=D(x)/n. Состоятельность докажем с помощью нер-ва Чебышева для выборочного среднего с учётом несмещённости: ρ(׀ ¯ x - M(X)׀>= ε) <= D(¯ x) / ε2 = D(x)/n ε2 для всякого ε>0. Поэтому limn→∞ ρ(׀ ¯ x - M(X)׀>= ε)=0. Отсюда limn→∞ ρ(׀ ¯ x - M(X)׀< ε)= 1 - limn→∞ ρ(׀ ¯ x - M(X)׀>= ε) = 1.
121. Пусть X1,…Xn – выборка из распр с дисперсией s2. Док-те, что Пусть Zn = (x1…xn) – случ выборка объема n, тогда исправленной выборочной дисперсией называется величина s2=n/(n-1) M(S2)=M(n/(n-1) M(
Что такое интервальная оценка для параметра q при доверительной вероятности g? Какой практический смысл имеет такая оценка, если g близка к 1? Как изменится доверительный интервал при уменьшении доверительной вероятности? Пусть q - неизвест пар-р или числовая хар-ка ген распр. Если выполняется Если g близка к 1, то такая оценка является надежной. При уменьшении g, d тоже уменьшается, значит, чтобы точно попасть в интервал его надо развинуть. 124. Пусть n X, X,..., X 1 2 – выборка из нормального распределения с математическим ожиданием m и дисперсией σ 2. Докажите, что для t > 0 интервал накрывает m с вероятностью 2 Ф (t), где Ф (t) – функция Лапласа. Пусть X1,..., Хn – выборка из нормального распределения Х с параметрами: M(X)=m, D(X)=σ2 тогда для t>0 доверит. интерв. (X-tσ/√n; X+tσ/√n), где Док-во: Связь между надежностью j и точностью оценки σ. По данному j найдем σ, так чтобы P(
X~N(m, σ2), P( 126 Укажите приближенный γ -доверительный интервал для доли признака в генеральной совокупности по относительной частоте. При каких n формула дает хорошее приближение?
Где Ф(t)=γ/2 n≥50
Какие события называются достоверными и невозможными и каковы их ве- роятности? Пусть A, B и C – случайные события. Перечислите все случаи наступления события Событие А, которое произойдет при любом испытании, называется достоверным (А = Событие А, которое не может произойти при испытании, называется невозможным (А=пуст.множ.). Например, событие А, задаваемое условием “при подбрасывании игральной кости выпало 7 очков”, является невозможным. Вероятность невозможного события равна 0. Таблица, характеризующая событие А
5.В каком случае событие В называют следствием события А? Какие события называются равными? Объясните, почему Событие А влечет за собой событие В или событие В является следствием события А (А I) А Если А наступило(А=1), то: 1) если В при этом наступило, то наступило АВ II) АВ+А Если АВ+А Событие А наступает, т.к. любое событие А попадает в В или
6. Пусть А и В – случайные события. Упростите выражение (А+В)(А+
7. Докажите, что
А
8. Докажите, что
А
9. Сформулируйте статистическое определение вероятности. Почему вероятность удовлетворяет условию Вероятность случайного события есть положительное число, заключенное между нулем и единицей. Случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0<m<n, значит, 0<m/n<1, следовательно, 0<P(A)<1. Вероятность любого события удовлетворяет двойному неравенству 0≤Р(А)≤1. В качестве статистической вероятности события понимают относительную частоту или число, близкое к ней. Свойства вероятносте
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 813; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.69.109 (0.009 с.) |

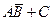 .
.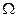 ). Например, в опыте с подбрасыванием игральной кости событие А, задаваемое условием “число выпавших очков положительное”, будет достоверным. Вероятность достоверного события равна 1.
). Например, в опыте с подбрасыванием игральной кости событие А, задаваемое условием “число выпавших очков положительное”, будет достоверным. Вероятность достоверного события равна 1. +С
+С .
. В), если каждый исход, благоприятный для А, является благоприятным и для В. События А и В равны (А=В) в случае, когда они являются следствиями друг друга.
В), если каждый исход, благоприятный для А, является благоприятным и для В. События А и В равны (А=В) в случае, когда они являются следствиями друг друга. АВ+А
АВ+А 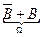 )=А*
)=А*  . Найдите событие, противоположное событию
. Найдите событие, противоположное событию 
 . Что обозначает событие
. Что обозначает событие 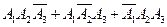 ?
? =
= 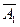 *
*  *…..*
*…..*  . Наступление события А
. Наступление события А 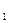 +….А
+….А 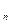 означает, что наступает по меньшей мере одно из событий А
означает, что наступает по меньшей мере одно из событий А 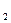
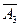 + А
+ А 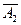 А
А 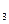 +
+ 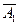 А
А  =
=  ? Возможны случаи Р=0 и Р=1? Ответ обоснуйте.
? Возможны случаи Р=0 и Р=1? Ответ обоснуйте.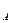 -благ.
-благ.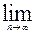
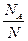 , где N
, где N 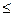 N, N
N, N 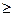 0.
0.
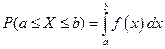
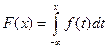
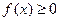 ,
, 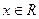 (неотрицательность).
(неотрицательность). (условие нормировки).
(условие нормировки).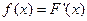 в точке непрерывности f(x).
в точке непрерывности f(x). находится пу-тем интегрирования произведения данной функции и плотности распределения:
находится пу-тем интегрирования произведения данной функции и плотности распределения: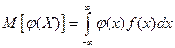

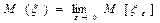 . Если указанный справа предел не существует, то мат. ожидание величины х также считается несуществующим.
. Если указанный справа предел не существует, то мат. ожидание величины х также считается несуществующим. , причем мат. ожидание существует, если ряд в правой части равенства сходится абсолютно. Т.к. ряд может и расходиться, то соотв. случайная величина может и не иметь мат. ожидания. На практике, как правило, множество возможных значений случайной величины распространяется лишь на ограниченный участок оси абсцисс и, значит, мат. ожидание существует.
, причем мат. ожидание существует, если ряд в правой части равенства сходится абсолютно. Т.к. ряд может и расходиться, то соотв. случайная величина может и не иметь мат. ожидания. На практике, как правило, множество возможных значений случайной величины распространяется лишь на ограниченный участок оси абсцисс и, значит, мат. ожидание существует.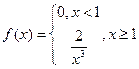 дисперсия D (X) не существует, а математическое ожидание M (X) существует.
дисперсия D (X) не существует, а математическое ожидание M (X) существует.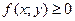 - плотность распределения, такая, что:
- плотность распределения, такая, что:
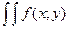 dxdy=1
dxdy=1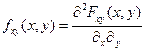 В точке непрерывности
В точке непрерывности 
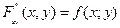 - в точках непрерывности f(x,y).
- в точках непрерывности f(x,y). кругу (if = если)
кругу (if = если)
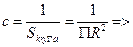
 кругу
кругу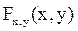 двумерного случайного вектора (X,Y), если известна функция плотности распределения f
двумерного случайного вектора (X,Y), если известна функция плотности распределения f  ? Укажите функцию распределения
? Укажите функцию распределения 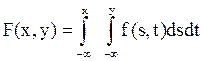
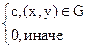
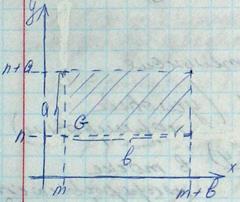

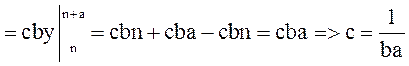

 т.к. иначе F(x,y), x>m+b, y>n+a, F(x,y)=1, x<m, y<n F(x,y=0]=
т.к. иначе F(x,y), x>m+b, y>n+a, F(x,y)=1, x<m, y<n F(x,y=0]=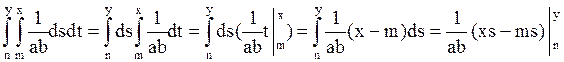 =
=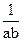 (x(y-n)-m(y-n))=
(x(y-n)-m(y-n))= 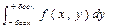 и соответственно наоборот.
и соответственно наоборот.

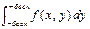 = 1/36
= 1/36 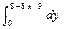 =
= 
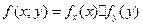
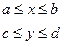 , в котором вектор (х,у) равномерно распределен.
, в котором вектор (х,у) равномерно распределен. иначе
иначе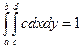 найдем
найдем 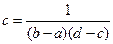
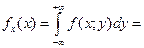
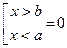
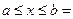
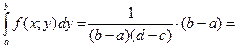
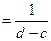
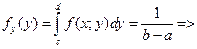
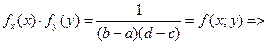
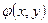 , где Х,У – компоненты случайного вектора (Х,У)? Как определяются начальные
, где Х,У – компоненты случайного вектора (Х,У)? Как определяются начальные  k,l и центральные
k,l и центральные 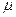 k,l моменты случайного вектора (Х,У)?
k,l моменты случайного вектора (Х,У)?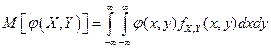

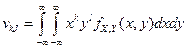
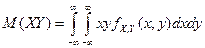 (1)
(1)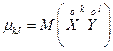
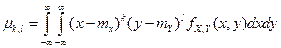
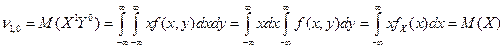
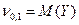
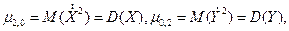
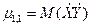
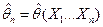 параметра
параметра 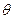 называется несмещенной, если
называется несмещенной, если 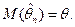 В противном случае оценка – смещенная.
В противном случае оценка – смещенная. 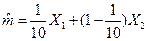 - является ли несмещенной оценкой?
- является ли несмещенной оценкой?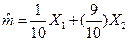
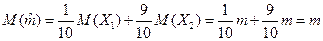
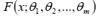 где
где 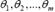 неизвестные параметры. Функцию
неизвестные параметры. Функцию  , которая при фиксированных значениях
, которая при фиксированных значениях 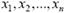 принимает значение, рассматриваемое как приближенное зна-чение неизвестного параметра θ генерального распределения, называют статистической оценкой па-раметра θ. По определению оценка является несмещенной, если ее математическое ожидание равно оцениваемому параметру. Эффективной называют оценку, которая при заданном объеме выборки п
принимает значение, рассматриваемое как приближенное зна-чение неизвестного параметра θ генерального распределения, называют статистической оценкой па-раметра θ. По определению оценка является несмещенной, если ее математическое ожидание равно оцениваемому параметру. Эффективной называют оценку, которая при заданном объеме выборки п  имеет наименьшую возможную дисперсию. Наконец, оценка называется состоятельной, если при она стремится (по вероятности) к оцениваемому параметру.
имеет наименьшую возможную дисперсию. Наконец, оценка называется состоятельной, если при она стремится (по вероятности) к оцениваемому параметру.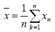
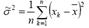

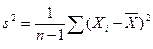 - несмещенная оценка s2.
- несмещенная оценка s2.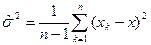 . Следствие: S2 – несмещенная оценка s2.
. Следствие: S2 – несмещенная оценка s2.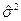 ) = n/(n-1) M(
) = n/(n-1) M(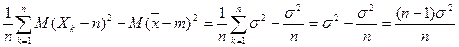 .
.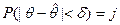 , то интервал
, то интервал 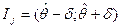 - называется доверительным интервалом, который покрывает неизвестный пар-р q ген распределения с доверительной вероятностью g (надежность оценки); d - точность оценки.
- называется доверительным интервалом, который покрывает неизвестный пар-р q ген распределения с доверительной вероятностью g (надежность оценки); d - точность оценки.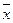 – выб. сред., а t – реш-е ур-ния Ф(t) = j/2, к-рый накрывает неизв. параметр m c над-тью j с вер-тью 2Ф(t), т.е. 2Ф(t)=j
– выб. сред., а t – реш-е ур-ния Ф(t) = j/2, к-рый накрывает неизв. параметр m c над-тью j с вер-тью 2Ф(t), т.е. 2Ф(t)=j Пусть р - доля признака генеральной совокупности, k/n-выборочная доля, тогда доверительный интервал равен:
Пусть р - доля признака генеральной совокупности, k/n-выборочная доля, тогда доверительный интервал равен: