
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
A и В? Для любых А и В? Запишите правило умножения вероятностей дляСодержание книги
Поиск на нашем сайте
трех (зависимых) событий A,B и C. Приведите примеры применения соответствующих формул. Для двух независимых событий А и В имеем Р(АВ)=Р(А)*Р(В)- правило умножения вероятностей для двух событий(тк для независ событий РB(А)=Р(А)). Вероятность произведения равна произведению вероятностей. Для двух любых событий А и В выполняется равенство Р(АВ)=РB(А)Р(В). Для трех любых событий: Р(АВС)=Р(А)РА(В)РАВ(С). Пример: 1)колода карт А- вытянем туза, В – вытянутая карта черной масти. Р(А)=4/36 2) В- выпало четное, А-выпала двойка Р(В)=1/2 РB(А)=1/3, Р(АВ)=РB(А)Р(В) Вероятность выпадения двойки 1/6.
Как определяется независимость в случае трех событий? Рассмотрите при- Мер: пусть в опыте с бросанием двух монет события A, В, С означают: А – на первой монете выпал герб; B – на второй монете выпал герб; C – обе монеты Упали на одну сторону. Будут ли независимы все три события? Почему? События А1, А2….Аn являются независимыми если вероятность любого из них не меняется при наступлении какого угодно числа событий из остальных. Р(АВ)=Р(А)*Р(В); Р(АС)=Р(А)*Р(С); Р(СВ)=Р(С)*Р(В) в системе Р(АВС)=Р(А)Р(В)Р(С) Все три события не будут независимы так как при событие С зависит от А и В: Если А и В произошли то Р(С)=1, если А и В не произошли Р(С)=1, а если А произошло а В нет и наоборот Р(С)=0.Поэтому справедливо Р(АВС)=Р(А)РА(В)РАВ(С)= 1/2*1/2*1=1/4 а не Р(АВС)=Р(А)Р(В)Р(С) 18. Как соотносятся понятия независимые события А и В и несовместные события А и В? Следует ли из независимости событий А,В,С независимость событий АВ и Если события независимы то вероятность их осуществления не меняется при наступлении любого количества из них. Если же события несовместны то наступление одного из них исключает наступление второго. В данном примере надо найти что АВ и АB=AB* P(AB)=P(ABC)+P(AB Р(АВ 19. События А и В независимы, события А и С также независимы. При этом события В и С несовместны. Следует ли из этого, что события А и В+С независимы? Ответ необходимо обосновать. В и С несовместны, т.е. Р(ВС)=0, т.к. В*С= Р(А*(В+С))=Р(А)*Р(В+С)-? + Р(АВ)+ Р(АС)=Р(А)*Р(В)+Р(А)*Р(С)=Р(А)*(Р(В)+Р(С))=Р(А)*Р(В+С)(из несовместности).ч.т.д. 20.События А и
В и С несовместны, т.е. Р(ВС)=0, т.к. В*С= Р(А*(В+С))=Р(А)*Р(В+С) -? 1. из того, что А и 2. из того, что А и Р(А)=Р(А Р(АВ)=Р(А)-Р(А) Р( Р(А(В+С)=Р(АВ+АС)=(А и С несовм)=Р(АВ)+Р(АС)=(А и В –независ, А и С-независ)= Р(А)*Р(В)+Р(А)*(Р(С))=Р(А)*(Р(В)+Р(С))=(В и С-несовм)=Р(А)*(Р(В+С)), ч.т.д.
21.Как определяется независимость событий А1,А2,……,Аn, в случае если n>2? Является ли равенство Р(А1А2А3)=Р(А1)*Р(А2)*Р(А3) достаточным для независимости событий А1,А2,А3? Ответ обоснуйте
События А1,А2,……,Аn называются независимыми в сов-ти, если для любого подмножества номеро/индексов:
Р(А i1 A i2 …A ik) =Р(А i1)…Р(A ik) Для независимости 3-х событий необходимо выполнить след. равенства. Р(АВ)=Р(А)Р(В) Р(АС)=Р(А)Р(С) Р(ВС)=Р(В)Р(С) Р(АВС)=Р(А)Р(В)Р(С)
22. Имеется две игральные кости: одна-симметричная, вторая-несимметричная. Пусть р- вероятность того, что при одновременном броске данных костей на них выпадет одинаковое число очков. Докажите, р= 1/6.
А-несимметр. кость
В чем состоит геометрический подход к определению вероятности? Как находится вероятность попадания в заданное множество, если точка случайно выбирается на отрезке AB? в треугольнике ABC? Геометрический подход заключается на предположении, что попадание каждой точки в геометрическом множестве( 1) Р(А)= 2)
24. В чем состоит геометрический подход к определению вероятности? Как на- Ходится вероятность попадания в заданное множество, если точка случайно
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 792; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.172.214 (0.005 с.) |

 ? Почему?
? Почему? .
.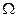 =AB(C+
=AB(C+ 

 независимы, события А и
независимы, события А и  также независимы. При этом события В и С несовместны. Следует ли из этого, что события А и В+С независимы? Ответ необходимо обосновать.
также независимы. При этом события В и С несовместны. Следует ли из этого, что события А и В+С независимы? Ответ необходимо обосновать. k≤n, выполняется:
k≤n, выполняется:



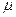 (А)), где
(А)), где 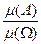 .
. .
.


