
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод подведения под знак дифференциала (устная замена переменной)Содержание книги
Поиск на нашем сайте
Интегральное исчисление 1.1 Первообразная, неопределенный интеграл Определение. Функция F(x) называется первообразной функции f(x) на множестве X, если Выражение F(x)+C представляет собой семейство всех первообразных функции f(x). (C=const). Определение. Если F(x) – одна из первообразных функции f(x), то выражение F(x)+C называется неопределенным интегралом. Обозначается Простейшие свойства. 1) 2) 3) 4) Таблица основных интегралов
В частности:
Из определения и свойств неопределенного интеграла следует, что дифференцирование и интегрирование являются взаимно обратными действиями: производная правой части в каждой формуле равна подынтегральной функции. Проверим, например, формулу 2.
Примеры: 1) 2) Методы интегрирования Метод подведения под знак дифференциала (устная замена переменной) Если относительно данной переменной интеграл не является табличным, то в некоторых случаях его можно привести к табличному относительно новой переменной с помощью подведения под знак дифференциала нужной функции. При этом удобно пользоваться следующими формулами, которые получаются из формул дифференцирования при прочтении их в обратном порядке:
Примеры (см. задание 1а) 1) 2) 3)
Метод письменной замены переменной (подстановки) План 1. Вводим новую переменную (подстановку) 2. Дифференцируем подстановку. 3. Вводим новую переменную в подынтегральное выражение. 4. Вычисляем интеграл. 5. Возвращаемся к старой переменной. Примеры (см. задание 1а): 1)
2)
3)
Метод интегрирования по частям Этот метод применяют для интегралов вида: а) б) в) где Формула интегрирования по частям имеет вид:
1) Для интегралов типа а) принимают U =P(x), все остальное равно dV. 2) Для интегралов типа б) принимают dV =P(x)dx. 3) для интегралов типа в) за U принимают любую функцию, метод применяют дважды. Примеры (см. задание 1б): 1)
2)
3)
4) можно решение записать иначе:
Получили первоначальный интеграл, обозначим его за y
Определенный интеграл Задача о площади. Вычислим площадь плоской фигуры, ограниченной графиком непрерывной, неотрицательной функции y=f(x), прямыми x=a, x=b, отрезком [ a,b ]. Такая фигура называется криволинейной трапецией. 1) Разобьем отрезок [ a, b ] произвольным образом на n частей точками 2) Через точки деления проведем вертикальные прямые. Трапеция разобьется на n трапеций. На каждом из элементарных отрезков выберем произвольным образом по точке Найдем значения функции в этих точках
Примем эти ординаты за высоты прямоугольников. 3) Посчитаем, что площади маленьких криволинейных трапеций приближенно равны площадям прямоугольников с основаниями
Чем мельче отрезки деления, тем точнее это равенство. За точное значение площади трапеции примем предел, к которому стремятся площади ступенчатых фигур при неограниченном увеличении числа отрезков деления и стремлении к нулю наибольшей из длин этих отрезков.
Понятие определенного интеграла К нахождению предела, рассмотренного в предыдущем пункте, приводит ряд задач естествознания. Поэтому рассмотрим предел, отвлекаясь от конкретного смысла задачи. Пусть на [ a, b ] задана произвольная функция y=f(x). Применяя для нее схему предыдущей задачи, составим сумму произведений вида
Такая сумма называется интегральной суммой функции f(x) на [ a, b ]. Она зависит от способа деления [ a, b ] на элементарные части и от выбора точек
Определение. Если существует конечный предел последовательности интегральных сумм при
_____________________________ Возвращаясь к задаче о площади криволинейной трапеции, получаем
т.е. при Теорема. Для любой непрерывной на [ a,b ] функции существует определенный интеграл.
Формула Ньютона-Лейбница Пусть f(x) – непрерывна на [ a, b ], F(x) – первообразная функции f(x) на [ a,b ], тогда определенный интеграл равен приращению первообразной (т.е. неопределенного интеграла) на этом отрезке:
Примеры 1) 2)
Интегрирование по частям (см. интегрирование по частям в разделе "Неопределенный интеграл") Формула интегрирования по частям для определенного интеграла имеет вид
Пример.
Основные понятия 1. Дифференциальным уравнением (ДУ) называется уравнение, связывающее независимую переменную, искомую функцию и ее производные:
2. Наивысший порядок производной искомой функции, входящей в ДУ, называется порядком ДУ. 3. Решить ДУ – это значит найти все функции, которые ему удовлетворяют, т. е. при подстановке их в уравнение, оно обращается в тождество. 4. Нахождение решений ДУ называется интегрированием ДУ, график решения ДУ называется интегральной кривой. Однородные функции Функция f(x,y) называется однородной k -ой степени однородности, если выполняется равенство:
В частности, если
Примеры 1)
2)
Коэффициентами Это уравнения вида
где Общее решение такого уравнения имеет вид
где
Определение. Функции Решение уравнения (1) сводится к решению алгебраического уравнения
называемого характеристическим, в котором степень k равна порядку производной в уравнении (1). При этом возможны следующие случаи: 1. При Они линейно независимы (смотри определение). Тогда общее решение (1) имеет вид:
2. При
3. Если Тогда частные решения Общее решение (1) имеет вид
Примеры (см. задание 5): 1)
2)
3)
4)
Ряды Ряд, сходимость, сумма. Пусть дана последовательность чисел Числовым рядом называется выражение
Сумма первых членов называется частичной суммой.
Частичные суммы образуют в свою очередь последовательность Ряд (1) называется сходящимся, если существует конечный предел последовательности частичных сумм S называется суммой ряда. Если этот предел не существует или равен бесконечности, то ряд называется расходящимся. Расходящиеся ряды суммы не имеют. Знакопеременные ряды Это ряды, содержащие как положительные, так и отрицательные члены. Частным случаем таких рядов являются знакочередующиеся ряды: ряды, в которых за каждым положительным членом следует отрицательный и за каждым отрицательным членом следует положительный:
или
Признак Лейбница. Если в знакочередующемся ряде 1) абсолютные величины членов ряда убывают 2) то знакочередующийся ряд сходится и его сумма не превосходит модуля первого члена. Следствие. Пусть знакочередующийся ряд сходится по признаку Лейбница. Если сумму этого ряда заменить суммой n первых членов, то погрешность, допускаемая при этом не превосходит модуля первого отброшенного члена. Рассмотрим знакочередующийся ряд Пример. Исследовать на условную и абсолютную сходимость ряд.
Это знакочередующийся ряд. Применим признак Лейбница. 1) 2) Исследуем ряд на условную и абсолютную сходимость. Для этого рассмотрим ряд, составленный из абсолютных величин данного ряда.
Степенные ряды Степенным рядом называется ряд вида:
где При a =0 имеем
При
Это уже числовой ряд. он может сходиться или расходиться. Если ряд (2) сходится, то Теорема Абеля. Для любого степенного ряда (1) существует интервал
Если R =0, то точка x =0 – единственная точка сходимости. Если R =¥, то ряд сходится на всей числовой оси. Пример. 1) Найти радиус и интервал сходимости степенного ряда. Исследовать сходимость ряда на концах интервала.
Тогда (-5; 5) – интервал, внутри которого ряд сходится абсолютно. Исследуем характер сходимости ряда на границах. 1) x =–5, тогда степенной ряд примет вид
Это знакочередующийся ряд. Для него применим признак Лейбница: 1)
2) x =5; (-5; 5) – область сходимости данного степенного ряда. 2)
1)
1) 2) 2)
Теория вероятностей Вероятность события Вероятностью события А называется отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всевозможных элементарных исходов испытания, т. е. 1) Пусть U – достоверное событие, тогда любой исход испытания благоприятен наступлению U, т. е. m=n, тогда P (U)=1. 2) V – невозможное событие, тогда ни один исход испытания не будет благоприятствующим, т. е. m= 0, тогда P (V)=0. 3) А – случайное событие, 0< m < n, тогда 0< P (A)<1. Пример. Монету бросаем два раза. Определить вероятность того, что герб появится не менее одного раза. Пусть А – событие, состоящее в появлении герба не менее одного раза. Элементарные исходы такие ГГ, ГЦ, ЦГ, ЦЦ, всего четыре исхода, из них благоприятствующих появлению события А – три, тогда Элементы комбинаторики 1. Пусть имеем три элемента a, b, c. Образуем из них комбинации (выборки) по два элемента: ab, ba, ac, ca, bc, cb – их шесть штук. Они отличаются друг от друга или элементами, или порядком следования элементов. Такие выборки называются размещениями, обозначаются
2. Выборки, отличающиеся друг от друга только порядком расположения элементов, называются перестановками, обозначаются
3. Выборки, отличающиеся одна от другой хотя бы одним элементом, называются сочетаниями, обозначаются
или
Следует помнить, что Пример. Среди 20 студентов группы, в которой 6 девушек, разыгрываются пять билетов. Определить вероятность того, что среди обладателей билетов окажутся две девушки. Решение. 5 билетов среди 20 человек можно распределить
Основные теоремы. Теоремы сложения 1. Вероятность наступления хотя бы одного из несовместных событий равна сумме вероятностей этих событий: P (A+B) =P (A) +P (B). 2. Вероятность наступления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления: P (A+B) =P (A) +P (B)– P (AB). Теоремы умножения Определения. 1) События называются независимыми, если вероятность наступления одного события не зависит от того, произошло другое событие или не произошло. 2) События называются зависимыми, если вероятность наступления одного из них зависит от того, произошло другое или нет. 3) Вероятность события А, вычисленная при условии, что событие В уже произошло, называется условной вероятностью, обозначается Теорема 1. Вероятность совместного наступления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже произошло.
или
Теорема 2. Вероятность совместного наступления независимых событий равна произведению вероятностей этих событий.
Задача. Из колоды в 36 карт наудачу одну за другой вынимают две карты. найти вероятность того, что будут вынуты два валета. Пусть А – событие, состоящее в том, что первая карта – валет; В – событие, состоящее в том, что вторая карта – валет; С – событие, состоящее в том, что вынуты два валета. Тогда Полная группа событий Если сумма событий Теорема. Если Определение. Два единственно возможных события, образующих полную группу, называются противоположными. Или: противоположным событию А называется событие Теорема. Сумма вероятностей двух противоположных событий равна 1: Если Вероятность наступления хотя бы одного события Теорема. Пусть А – событие, состоящее в появлении хотя бы одного из событий Задача. Три станка работают независимо друг от друга. Вероятность того, что первый станок в течение часа выйдет из строя, равна 0,015, для второго и третьего станков эти вероятности равны 0,02 и 0,025. Найти вероятность того, что в течение часа хотя бы один станок выйдет из строя. Пусть
А – событие, состоящее в том, что хотя бы один из станков выйдет из строя.
Тогда Формула полной вероятности Пусть событие А может произойти только с одним из событий
Задача. С первого автомата на сборку поступает 20%, со второго – 30%, с третьего – 50% всех деталей. Первый автомат дает в среднем 0,2% брака, второй – 0,3%, третий – 0,1%. Найти вероятность того, что наудачу взятая со сборки деталь будет бракованная. Пусть
Формула Бейеса Пусть выполнены все условия предыдущей теоремы. Но пусть уже известно, что событие А – произошло. Тогда вероятность гипотезы после опыта определяется по формуле:
P (A) находим по формуле полной вероятности. Задача. Два автомата производят одинаковые детали, которые собираются на общий конвейер. Производительность первого автомата в два раза больше второго. Первый производит в среднем 60% деталей отличного качества, второй – 84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что она изготовлена вторым автоматом.
Тогда
Формула Бернулли Пусть произведено n независимых испытаний, в каждом из которых событие А может появиться с вероятностью P (A)= p, причем
где Задача. Орудие стреляет по цели пять раз. Вероятность попадания при одном выстреле равна 0,6. Найти вероятность того, что орудие попадает два раза.
Случайные величины Случайной величиной называют такую величину, которая в результате испытания принимает одно и только одно из возможных своих значений, заранее неизвестное и зависящее от случайных обстоятельств, которые не всегда можно учесть. Обозначается X, Y, Z, …, возможные ее значения обозначаются Случайные величины бывают дискретные и непрерывные. Дискретная случайная величина принимает отдельные изолированные возможные значения с определенными вероятностями. Соответствие между возможными значениями дискретной случайной величины и их вероятностями называется законом или рядом распределения. Пример. Бросаем игральную кость. Случайная величина X – число выпавших очков, ее возможные значения 1, 2, 3, 4, 5, 6. Любое из этих значений появляется с вероятностью
– ряд распределения случайной величины. Так как в каждом испытании случайная величина обязательно примет одно из возможных своих значений, то события Пример (см. задание 8). Составить закон распределения числа отказавших элементов прибора, если элементов три, а вероятность отказа каждого, независимо работающего элемента равна 0,2. Пусть случайная величина X – число отказавших элементов, ее возможные значения:
Тогда закон распределения этой случайной величины принимает вид:
Контроль: Числовые характеристики Математическим ожиданием дискретной случайной величины называется сумма произведений возможных значений случайной величины на вероятности этих возможных значений. Обозначается:
Математическое ожидание – это число, центр распределения случайной величины, – ее возможные значения расположены на оси левее и правее математического ожидания. Дисперсией дискретной случайной величины называется математическое ожидание квадрата отклонения этой случайной величины от своего математического ожидания.
Можно доказать, что
Этой формулой удобно пользоваться в расчетах. Дисперсия характеризует меру рассеяния возможных значений случайной величины относительно ее математического ожидания. Средним квадратическим отклонением называется Пример. (см. задание 8). Дан ряд распределения случайной величины. Найти | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

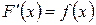 для всех
для всех 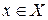 .
.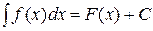 .
.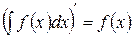
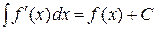
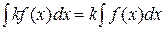
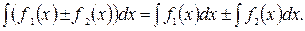
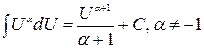 .
.
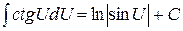 .
.
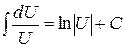 .
.
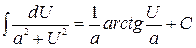 .
.
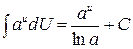 .
.
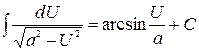 .
.
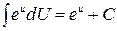 .
.
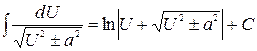 .
.
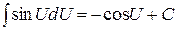 .
.
 .
.
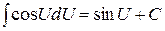 .
.
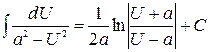 .
.
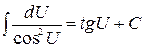 .
.
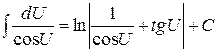 .
.
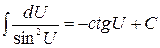 .
.
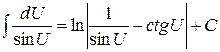 .
.
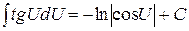 .
.
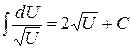 ;
; 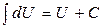 ;
; 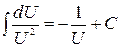 .
.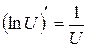
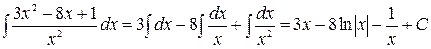 ;
;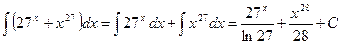 .
.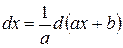
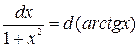
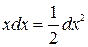
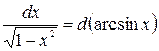
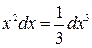
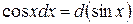
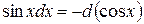
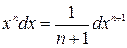 , n ≠-1
, n ≠-1
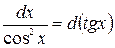
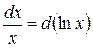
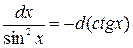
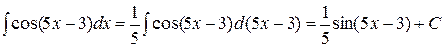 ;
;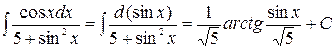
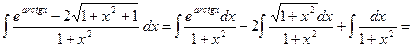


 .
.


 .
.
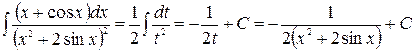 .
.
 ,
,  ,
, 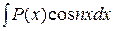 ;
; ,
,  ,
, 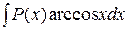 ,
, 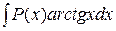 ,
,  ;
; ,
,  ;
; - многочлен.
- многочлен. .
. ;
;

 ;
;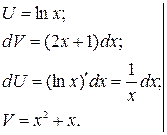

 .
.

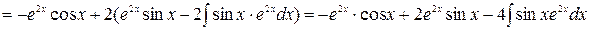
 ;
; ;
; +С.
+С. . Получим n маленьких отрезков с длинами
. Получим n маленьких отрезков с длинами 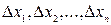 ;
;  .
. .
. .
. и высотами
и высотами  . Тогда
. Тогда .
. .
. .
. на каждой из этих частей.
на каждой из этих частей. , не зависящий от способа деления [ a, b ] и выбора точек
, не зависящий от способа деления [ a, b ] и выбора точек  , то этот предел (число) называется определенным интегралом от функции f(x) на [ a, b ] и обозначается
, то этот предел (число) называется определенным интегралом от функции f(x) на [ a, b ] и обозначается

 определенный интеграл численно равен площади криволинейной трапеции. В этом состоит геометрический смысл определенного интеграла.
определенный интеграл численно равен площади криволинейной трапеции. В этом состоит геометрический смысл определенного интеграла.
 ;
;




 .
. .
. – функция однородная нулевой степени однородности.
– функция однородная нулевой степени однородности. .
. – однородная функция второй степени однородности.
– однородная функция второй степени однородности.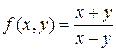 .
.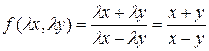 – однородная функция нулевой степени однородности.
– однородная функция нулевой степени однородности. ,
,
 – константы.
– константы.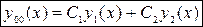
 – произвольные постоянные
– произвольные постоянные -общее решение однородного уравнения,
-общее решение однородного уравнения, -линейно независимые частные решения уравнения (1).
-линейно независимые частные решения уравнения (1). и
и  называются линейно независимыми (зависимыми) на (a, b), если при
называются линейно независимыми (зависимыми) на (a, b), если при 

 ,
,
 уравнение (2) имеет действительные различные корни
уравнение (2) имеет действительные различные корни  , тогда частные решения ДУ (1) имеют вид
, тогда частные решения ДУ (1) имеют вид  ,
,  (в чем можно убедится непосредственной подстановкой).
(в чем можно убедится непосредственной подстановкой).
 характеристическое уравнение (2) имеет два действительных равных корня
характеристическое уравнение (2) имеет два действительных равных корня 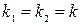 , тогда частными решениями Д.У. (1) являются функции
, тогда частными решениями Д.У. (1) являются функции  , общее решение (1) имеет вид
, общее решение (1) имеет вид
 , то характеристическое уравнение (2) не имеет действительных корней, но имеет комплексные корни вида
, то характеристическое уравнение (2) не имеет действительных корней, но имеет комплексные корни вида  .
.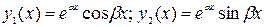

 , составим характеристическое уравнение:
, составим характеристическое уравнение: 
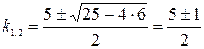 ;
;  ;
;  .
.
 , составим характеристическое уравнение
, составим характеристическое уравнение 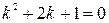
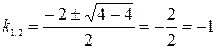 ;
; ;
; .
.

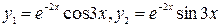

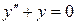

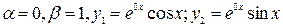


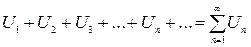 . (1)
. (1)
 , которая для одних рядов сходится, для других – расходится.
, которая для одних рядов сходится, для других – расходится. .
.
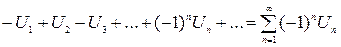 .
.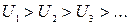 ;
;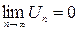 ,
,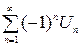 и ряд, составленный из абсолютных его величин. Если ряд, составленный из абсолютных величин, сходится, то знакопеременный ряд называется абсолютно сходящимся рядом. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин, расходится, то знакопеременный ряд называется условно сходящимся.
и ряд, составленный из абсолютных его величин. Если ряд, составленный из абсолютных величин, сходится, то знакопеременный ряд называется абсолютно сходящимся рядом. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин, расходится, то знакопеременный ряд называется условно сходящимся.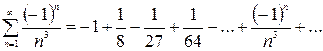
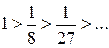 ;
;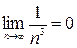 . => ряд сходится по признаку Лейбница.
. => ряд сходится по признаку Лейбница. – это обобщенный гармонический ряд, он сходится, так как k =3>1, тогда знакочередующийся ряд
– это обобщенный гармонический ряд, он сходится, так как k =3>1, тогда знакочередующийся ряд 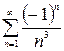 является абсолютно сходящимся рядом.
является абсолютно сходящимся рядом.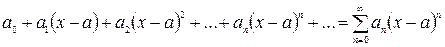 ,
,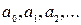 – постоянные величины, коэффициенты ряда, число a – центр ряда.
– постоянные величины, коэффициенты ряда, число a – центр ряда.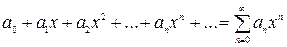
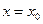 степенной ряд (1) принимает вид
степенной ряд (1) принимает вид
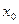 – точка сходимости степенного ряда (1). Если ряд (2) расходится, то
– точка сходимости степенного ряда (1). Если ряд (2) расходится, то 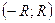 , внутри которого ряд сходится абсолютно, вне его расходится, а на границах может иметь различный характер сходимости.
, внутри которого ряд сходится абсолютно, вне его расходится, а на границах может иметь различный характер сходимости.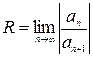 – радиус интервала сходимости.
– радиус интервала сходимости.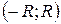 – интервал сходимости.
– интервал сходимости.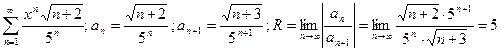 .
.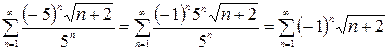 .
.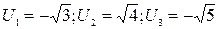
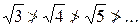 – не выполнено первое условие признака Лейбница, тогда ряд
– не выполнено первое условие признака Лейбница, тогда ряд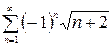 расходится, точка
расходится, точка 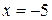 – точка расходимости.
– точка расходимости.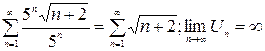 – ряд расходится по следствию из необходимого признака, тогда x =5 – точка расходимости.
– ряд расходится по следствию из необходимого признака, тогда x =5 – точка расходимости.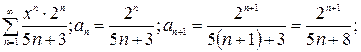
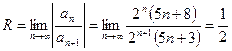 .
.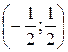 – интервал сходимости данного степенного ряда. Исследуем на границах:
– интервал сходимости данного степенного ряда. Исследуем на границах: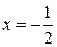 , тогда степенной ряд примет вид:
, тогда степенной ряд примет вид: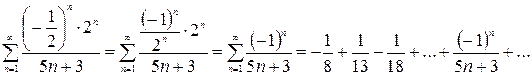 – это знакочередующийся ряд. Проверим два условия:
– это знакочередующийся ряд. Проверим два условия: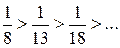 ;
;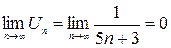 , тогда ряд
, тогда ряд 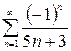 сходится по признаку Лейбница, точка
сходится по признаку Лейбница, точка 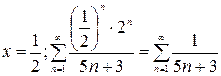 . Сравним этот ряд с гармоническим
. Сравним этот ряд с гармоническим 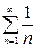 , который, как известно, расходится.
, который, как известно, расходится.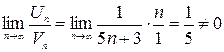 – конечное число, тогда по следствию из признака сравнения ряды ведут себя одинаково, т. е. оба расходятся, поэтому точка
– конечное число, тогда по следствию из признака сравнения ряды ведут себя одинаково, т. е. оба расходятся, поэтому точка 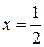 – точка расходимости начального степенного ряда.
– точка расходимости начального степенного ряда.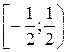 – область сходимости степенного ряда.
– область сходимости степенного ряда.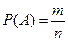 , где m – число элементарных исходов, при которых наступает событие А (благоприятствующие исходы), n – число всех возможных исходов данного испытания. Это классическое определение вероятности события.
, где m – число элементарных исходов, при которых наступает событие А (благоприятствующие исходы), n – число всех возможных исходов данного испытания. Это классическое определение вероятности события. , т. е.
, т. е. .
. .
. .
. .
.
 .
. ,
, .
.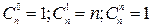 .
. способами. 3 билета среди 14 юношей можно распределить
способами. 3 билета среди 14 юношей можно распределить  способами, 2 билета среди 6 девушек можно распределить
способами, 2 билета среди 6 девушек можно распределить 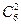 способами. Каждая пара девушек может сочетаться с любой тройкой юношей, т. е. число благоприятных исходов
способами. Каждая пара девушек может сочетаться с любой тройкой юношей, т. е. число благоприятных исходов 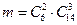 , а число всех возможных исходов
, а число всех возможных исходов  . Тогда
. Тогда .
. (читается: «Р от А при условии, что В произошло»).
(читается: «Р от А при условии, что В произошло»).
 .
. .
.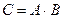 . События А и В – зависимые, тогда
. События А и В – зависимые, тогда  .
. есть достоверное событие (т. е., в результате испытания хотя бы одно из них непременно произойдет), то события
есть достоверное событие (т. е., в результате испытания хотя бы одно из них непременно произойдет), то события  образуют полную группу событий. Если эти события попарно несовместны, то
образуют полную группу событий. Если эти события попарно несовместны, то  .
. , состоящее в ненаступлении А (читается «не А»).
, состоящее в ненаступлении А (читается «не А»). .
.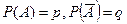 , то p+q= 1.
, то p+q= 1. .
. – событие, состоящее в том, что первый станок в течении часа выйдет из строя;
– событие, состоящее в том, что первый станок в течении часа выйдет из строя; – второй;
– второй; – третий;
– третий;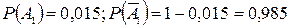 ;
; ;
; .
. .
. , которые образуют полную группу попарно несовместных событий. События
, которые образуют полную группу попарно несовместных событий. События  называются гипотезами. Пусть известны вероятности гипотез
называются гипотезами. Пусть известны вероятности гипотез  и условные вероятности события А по гипотезам, т. е.
и условные вероятности события А по гипотезам, т. е.  , тогда
, тогда .
. – событие, состоящее в том, что наудачу взятая деталь изготовлена на первом автомате,
– событие, состоящее в том, что наудачу взятая деталь изготовлена на первом автомате,  – на втором,
– на втором,  – на третьем. А – событие, состоящее в том, что наудачу взятая со сборки деталь будет бракованная.
– на третьем. А – событие, состоящее в том, что наудачу взятая со сборки деталь будет бракованная. ,
, 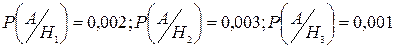 ,
,
 .
. – событие, состоящее в том, что наудачу взятая деталь изготовлена первым автоматом,
– событие, состоящее в том, что наудачу взятая деталь изготовлена первым автоматом,  – вторым. А – событие, состоящее в том, что наудачу взятая деталь отличного качества.
– вторым. А – событие, состоящее в том, что наудачу взятая деталь отличного качества. ;
;
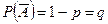 . Последовательность появления события А не имеет значения. Тогда вероятность того, что в n независимых испытаниях событие А наступает ровно m раз вычисляется по формуле:
. Последовательность появления события А не имеет значения. Тогда вероятность того, что в n независимых испытаниях событие А наступает ровно m раз вычисляется по формуле: ,
, .
. .
. . Тогда:
. Тогда: образуют полную группу попарно несовместных событий, а поэтому
образуют полную группу попарно несовместных событий, а поэтому  .
. ,
, ,
,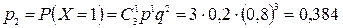 ,
,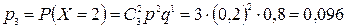 ,
, .
.
 .
. .
. .
. .
.


