
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод письменной замены переменной (подстановки)
План 1. Вводим новую переменную (подстановку) 2. Дифференцируем подстановку. 3. Вводим новую переменную в подынтегральное выражение. 4. Вычисляем интеграл. 5. Возвращаемся к старой переменной. Примеры (см. задание 1а): 1)
2)
3)
Метод интегрирования по частям Этот метод применяют для интегралов вида: а) б) в) где Формула интегрирования по частям имеет вид:
1) Для интегралов типа а) принимают U =P(x), все остальное равно dV. 2) Для интегралов типа б) принимают dV =P(x)dx. 3) для интегралов типа в) за U принимают любую функцию, метод применяют дважды. Примеры (см. задание 1б): 1)
2)
3)
4) можно решение записать иначе:
Получили первоначальный интеграл, обозначим его за y
Определенный интеграл Задача о площади. Вычислим площадь плоской фигуры, ограниченной графиком непрерывной, неотрицательной функции y=f(x), прямыми x=a, x=b, отрезком [ a,b ]. Такая фигура называется криволинейной трапецией. 1) Разобьем отрезок [ a, b ] произвольным образом на n частей точками 2) Через точки деления проведем вертикальные прямые. Трапеция разобьется на n трапеций. На каждом из элементарных отрезков выберем произвольным образом по точке Найдем значения функции в этих точках
Примем эти ординаты за высоты прямоугольников. 3) Посчитаем, что площади маленьких криволинейных трапеций приближенно равны площадям прямоугольников с основаниями
Чем мельче отрезки деления, тем точнее это равенство. За точное значение площади трапеции примем предел, к которому стремятся площади ступенчатых фигур при неограниченном увеличении числа отрезков деления и стремлении к нулю наибольшей из длин этих отрезков.
Понятие определенного интеграла К нахождению предела, рассмотренного в предыдущем пункте, приводит ряд задач естествознания. Поэтому рассмотрим предел, отвлекаясь от конкретного смысла задачи. Пусть на [ a, b ] задана произвольная функция y=f(x). Применяя для нее схему предыдущей задачи, составим сумму произведений вида
Такая сумма называется интегральной суммой функции f(x) на [ a, b ]. Она зависит от способа деления [ a, b ] на элементарные части и от выбора точек
Определение. Если существует конечный предел последовательности интегральных сумм при
_____________________________ Возвращаясь к задаче о площади криволинейной трапеции, получаем
т.е. при Теорема. Для любой непрерывной на [ a,b ] функции существует определенный интеграл.
Свойства определенного интеграла 1) 3) 5) 6) Если Если Следствие. Если 7) Если f(x) непрерывна на [ a, b ], m, M - ее соответственно наименьшее и наибольшее значение на [ a, b ], то справедлива оценка
8) (Теорема о среднем). Если f(x) непрерывна на [ a, b ], то существует хотя бы одна точка
Формула Ньютона-Лейбница Пусть f(x) – непрерывна на [ a, b ], F(x) – первообразная функции f(x) на [ a,b ], тогда определенный интеграл равен приращению первообразной (т.е. неопределенного интеграла) на этом отрезке:
Примеры 1) 2)
Интегрирование по частям (см. интегрирование по частям в разделе "Неопределенный интеграл") Формула интегрирования по частям для определенного интеграла имеет вид
Пример.
Замена переменной в определенном интеграле Теорема. Пусть f(x) непрерывна на [ a, b ], введем подстановку 1) 2) при изменении t от
Пример (см. задание 2):
Вычисление площадей плоских фигур
Эта формула остается справедливой при любом расположении рассматриваемой фигуры.
Пример (см. задание 3):
1) Найдем точки пересечения данных кривых.
2) Построим графики данных функций.
Основные понятия
1. Дифференциальным уравнением (ДУ) называется уравнение, связывающее независимую переменную, искомую функцию и ее производные:
2. Наивысший порядок производной искомой функции, входящей в ДУ, называется порядком ДУ. 3. Решить ДУ – это значит найти все функции, которые ему удовлетворяют, т. е. при подстановке их в уравнение, оно обращается в тождество. 4. Нахождение решений ДУ называется интегрированием ДУ, график решения ДУ называется интегральной кривой.
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 222; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.221.67 (0.116 с.) |

 .
.


 .
.
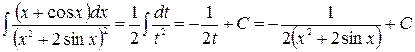 .
.
 ,
,  ,
, 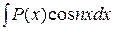 ;
; ,
,  ,
, 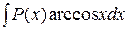 ,
, 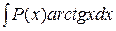 ,
,  ;
; ,
,  ;
; - многочлен.
- многочлен. .
. ;
;

 ;
;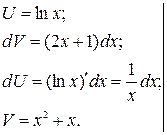

 .
.

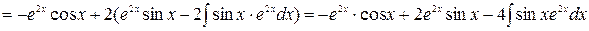
 ;
; ;
; +С.
+С. . Получим n маленьких отрезков с длинами
. Получим n маленьких отрезков с длинами 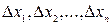 ;
;  .
. .
. .
. и высотами
и высотами  . Тогда
. Тогда .
. .
. .
. на каждой из этих частей.
на каждой из этих частей. , не зависящий от способа деления [ a, b ] и выбора точек
, не зависящий от способа деления [ a, b ] и выбора точек  , то этот предел (число) называется определенным интегралом от функции f(x) на [ a, b ] и обозначается
, то этот предел (число) называется определенным интегралом от функции f(x) на [ a, b ] и обозначается

 определенный интеграл численно равен площади криволинейной трапеции. В этом состоит геометрический смысл определенного интеграла.
определенный интеграл численно равен площади криволинейной трапеции. В этом состоит геометрический смысл определенного интеграла. ; 2)
; 2)  ;
; ; 4)
; 4)  ;
; ;
; ;
; , то
, то  .
. , то
, то  .
.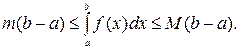
 такая, что
такая, что

 ;
;




 . Если
. Если непрерывны при
непрерывны при  ,
, до
до  , функция
, функция  изменяется от a до b,
изменяется от a до b,  , то справедлива формула замены переменной:
, то справедлива формула замены переменной:
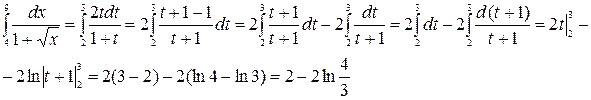
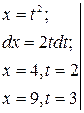


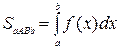 – площадь криволинейной трапеции.
– площадь криволинейной трапеции. Площадь фигуры, ограниченной линиями
Площадь фигуры, ограниченной линиями  , находим по формуле
, находим по формуле
 Вычислить площадь фигуры, ограниченной линиями:
Вычислить площадь фигуры, ограниченной линиями:  ,
,  .
.
 ;
; ;
; ;
; ;
;  .
.
 (для прямой
(для прямой 

 (парабола
(парабола  ).
). 4 Дифференциальные уравнения
4 Дифференциальные уравнения .
.


