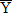Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод моментов для точечной оценки параметров распределения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Метод моментов оценивания параметров распределения генеральной совокупности состоит в том, на основании выборки х1, х2,..., хn вычисляются выборочные моменты (начальные или центральные). Полученные значения приравниваются соответствующим теоретическим моментам. Количество моментов должно ровняться числу оцениваемых параметров. Затем решают полученную систему уравнений относительно этих параметров. Рассмотрим случай, когда метод моментов используется для нахождения оценки одного параметра. Положим, что плотность распределения f (x; a) случайной величины Х зависит только от одного параметра а, и необходимо найти оценку параметра а. Для нахождения оценки одного параметра достаточно иметь одно уравнение относительно этого параметра, используя, например, на основании выборки х1, х2,...,, хn первый начальный момент
Приравняем его значение первому теоретическому моменту
рассматривая правую часть равенства как функцию от а. Решая это уравнение относительно неизвестного параметра а, получаем точечную оценку
Пример. Пусть Х – непрерывная случайная величина подчинена показательному (экспоненциальному) закону, плотность распределения которого зависит от одного неизвестного параметра
Используя полученные экспериментальные данные х1, х2,..., хn, получить оценку параметра Решение. На основании выборки х1, х2,..., хn находим первый выборочный момент и приравниваем его первому моменту случайной величины Х, подчиненной показательному закону:
Отсюда получаем оценку параметра
Если функция плотности распределения случайной величины Х зависит от двух параметров, например Примеры. 1. По выборке х1, х2,..., хп методом моментов найти точечные оценки параметров mx и
Решение. Так как первый начальный момент нормального распределения равен параметру тх., а второй центральный момент равен параметру то
2. По выборке х1, х2,..., хп методом моментов найти точечные оценки параметров а1, а2 равномерного распределения на интервале [ а1, а2 ]:
Решение. Используя выборку х1, х2,..., хп, находим выборочные первый начальный и второй центральные моменты:
Для равномерного распределения имеем теоретические моменты
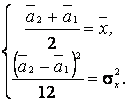
Прировняем теоретические моменты выборочным и получаем систему двух уравнений с двумя неизвестными для нахождения оценок параметров а1, а2:
Решая эту систему, получаем в окончательном виде
где величины 26. Функциональная, статистическая и корреляционная зависимости. Пусть у нас имеются n серии значений двух параметров X и Y: (x1;y1),(x2;y2),...,(xn;yn). Подразумевается, что у одного и того же объекта измерены два параметра. Нам надо выяснить есть ли значимая связь между этими параметрами. Как известно, случайные величины X и Y могут быть либо зависимыми, либо независимыми. Существуют следующие формы зависимости – функциональная и статистическая. В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y=f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y. Однако, если X и Y случайные величины, то между ними может существовать зависимость иного рода, называемая статистической. Дело в том, что на формирование значений случайных величин X и Y оказывают влияние различные факторы. Под воздействием этих факторов и формируются конкретные значения X и Y. Допустим, что на Х и У влияют одни те же факторы, например Z1, Z2, Z3, тогда X и Y находятся в полном соответствии друг с другом и связаны функционально. Предположим теперь, что на X воздействуют факторы Z1, Z2, Z3, а на только Y и Z1, Z2. Обе величины и X и Y являются случайными, но так как имеются общие факторы Z1 и Z2, оказывающие влияние и на X и на Y, то значения X и Y обязательно будут взаимосвязаны. И связь это уже не будет функциональной: фактор Z3, влияющий лишь на одну из случайных величин, разрушает прямую (функциональную) зависимость между значениями X и Y, принимаемыми в одном и том же испытании. Связь носит вероятностный случайный характер, в численном выражении меняясь, от испытания к испытанию, но эта связь определенно присутствует и называется статистической. При этом каждому значению X может соответствовать не одно значение Y, как при функциональной зависимости, а целое множество значений. ОПРЕДЕЛЕНИЕ. Зависимость случайных величин называют статистической, если изменения одной из них приводит к изменению закона распределения другой. ОПРЕДЕЛЕНИЕ. Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные коррреляционной зависимостью, оказываются коррелированными. Примерами коррреляционной зависимости являются: зависимость массы от роста: Корреляционную зависимость Y от X можно описать с помощью уравнения вида: yx=f(x) (1) где yx - условное среднее величины Y, соответствующее значению x величины X, а f(x) некоторая функция. Уравнение (1) называется выборочным уравнением регрессии Y на X. Функцию f(x) называют выборочной регрессией Y на X, а ее график – выборочной линией регрессии Y на X. Совершенно аналогично выборочным уравнением регрессии X на Y является уравнение: xy=φ(y) В зависимости от вида уравнения регрессии и формы соответствующей линии регрессии определяют форму корреляционнной зависимости между рассматриваемыми величинами – линейной, квадратической, показательной, экспоненциальной. Важнейшим является вопрос выбора вида функции регрессии f(x) [или φ(y)], например линейная или нелинейная (показательная, логарифимическая и т.д.) На практике вид функции регрессии можно определить, построив на координатной плоскости множество точек, соответствующих всем имеющимся парам наблюдений (x;y).
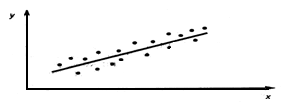
Рис. 1. Линейная регрессия значима. Модель Y=a+bX.
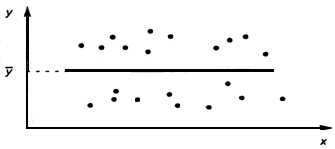
Рис. 2. Линейная регрессия незначима. Модель Y=
Рис. 3. Линейная регрессия значима. Нелинейная модель (y=ax2+bx+c) Например, на рис.1. видна тенденция роста значений Y с ростом X, при этом средние значения Y располагается визуально на прямой. Имеет смысл использовать линейную модель (вид зависимости Y от X принято называть моделью) зависимости Y от X. На рис.2. средние значения Y не зависят от x, следовательно линейная регрессия незначима (функция регрессии постоянна и равна 27. Условные средние выборочные уравнения регрессии. Во многих задачах требуется установить и оценить зависимость изучаемой слу- чайной величины Y от одной или нескольких других величин. Рассмотрим сначала зависимость Y от одной случайной (или неслучайной) величины X. Две случайные величины могут быть связаны либо функциональ- ной зависимостью, либо зависимостью другого рода, называемой статистиче- ской, либо быть независимыми. Строгая функциональная зависимость реализуется редко, так как обе вели- чины или одна из них подвержены еще действию случайных факторов, причем среди них могут быть и общие для обеих величин (под общими здесь подразу- меваются такие факторы, которые воздействуют и на Y и на X). В этом случае возникает статистическая зависимость. Например, если Y зависит от случайных факторов Z1, Z2, V1, V2, a X зависит от случайных факторов Z1, Z2, U1, U2, то между Y и X имеется ста- тистическая зависимость, так как среди случайных факторов есть общие: Z1 и Z2. Определение 71. Статистической называют зависимость, при которой из- менение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при из- менении одной из величин изменяется среднее значение другой; в этом случае статистическую зависимость называют корреляционной. Рассмотрим пример случайной величины Y, которая не связана с величи- ной X функционально, а связана корреляционно. Пусть Y - урожай зерна, X - количество удобрений. С одинаковых по площади участков земли при рав- ных количествах внесенных удобрений снимают различный урожай, т. е. Y не является функцией от X. Это объясняется влиянием случайных факторов (осадки, температура возду- ха и др.). Вместе с тем, как показывает опыт, средний урожай является функци- ей от количества удобрений, т. е. Y связан с X корреляционной зависимостью. 15.1.2. Условные средние В качестве оценок условных математических ожиданий принимают условные средние, которые находят по данным наблюдений (по выборке). Определение 72. Условным средним yx называется среднее арифметическое наблюдавшихся значений Y, соответствующих X = x. Пример. Если при x1 = 2 величина Y приняла значения y1 = 5, y2 = 6, y3 = 10, то условное среднее yx1 =5 + 6 + 10/3= 7 Аналогично определяется условное среднее xy.15.1. Теория корреляций 119 Определение 73. Условным средним xy называется среднее арифметическое наблюдавшихся значений X, соответствующих Y = y. 15.1.3. Выборочные уравнения регрессии При изучении условных вероятностей мы вводили понятие условного математи- ческого ожидания Условным математическим ожиданием дискретной случайной величины Y при X = x (x - определенное возможное значение X) называется произведе- ние возможных значений Y на их условные вероятности: M[Y|X = x] = Xm j=1 yjp(yj|x). Для непрерывных величин M[Y |X = x] = Z ∞ −∞ yψ(y|x)dy, где ψ(y|x) - условная плотность случайной величины Y при X = x. Условное математическое ожидание M[Y|X = x] есть функция от x: M[Y|X = x] = M[Y|x] = f(x), которая называется функцией регрессии Y на X. Аналогично определяются условное математическое ожидание случайной ве- личины X и функция регрессии X на Y: M[X|Y = y] = M[X|y] = ϕ(y). Условное математическое ожидание M[Y |x] является функцией от x, следова- тельно, его оценка, т. е. условное среднее yx , также функция от x; обозначив эту функцию через f ∗ (x), получим уравнение yx = f ∗ (x). Определение 74. Выборочным уравнением регрессии Y на X называется уравнение yx = f ∗ (x). Выборочной регрессией Y на X называется функция f ∗ (x). Выборочной линией регрессии Y на X называется график функции f ∗ (x). Аналогично уравнение xy = ϕ ∗ (y). называется выборочным уравнением регрессии X на Y; функция ϕ ∗ (y) называ- ется выборочной регрессией X на Y, а ее график - выборочной линией регрессии X на Y. 28. Построение линейных моделей: 1)по не сгруппированным выборочным данным. 2) по сгруппированным выборочным даннымю Для того, чтобы найти объясненную часть, т. е. величину математического ожидания Мх(У), требуется нахождение условных распределений случайной величины Y. На практике это почти никогда не возможно. В большинстве случаях при решении задач по эконометрике применяется стандартная процедура сглаживания экспериментальных данных. Эта процедура состоит из двух этапов: 1) определяется параметрическое семейство, к которому принадлежит искомая функция Мх(У) (определяемая как функция от значений объясняющих переменных X). Это может быть линейная функция, показательная функция и т.д.; 2) находятся оценки параметров этой функции с помощью одного из методов мат. статистики. Формально никаких способов выбора параметрического семейства нет. Однако в большинстве случаев модели в задачах предмета эконометрика выбираются линейными. Кроме очевидного преимущества линейной модели — ее относительной простоты, — для этого выбора имеются, как минимум, две существенные причины. Первая причина: если случайная величина (X, У) имеет совместное нормальное распределение, то уравнения регрессии линейные. В других случаях сами величины Y или X могут не иметь нормального распределения, но некоторые функции от них распределены нормально. Например, известно, что логарифм доходов на душу населения — нормально распределенная случайная величина. В большинстве случаев гипотеза о нормальном распределении принимается, когда нет явного ей противоречия, и, как показывает практика, подобная предпосылка бывает вполне разумной. Вторая причина, по которой линейная регрессионная модель оказывается предпочтительнее других, является меньший риск значительной ошибки прогноза.
Рисунок показывает два выбора функции регрессии — линейной и квадратичной. Как видно, имеющееся множество экспериментальных данных (точек) парабола сглаживает, пожалуй, даже лучше, чем прямая. Однако парабола быстро удаляется от корреляционного поля и для добавленного наблюдения теоретическое значение может очень значительно отличаться от эмпирического. Можно определить точный математический смысл этому утверждению: ожидаемое значение ошибки прогноза, т.е. математическое ожидание квадрата отклонения наблюдаемых значений от сглаженных (или теоретических) оказывается меньше в том случае, если выбрано линейное уравнение регрессии.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.219.213 (0.01 с.) |

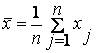 .
. =
= 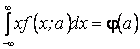 ,
, , которая теперь является функцией от вариант выборки, то есть
, которая теперь является функцией от вариант выборки, то есть .
. :
: , х
, х 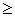 0.
0.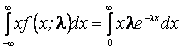 =
=  .
. .
.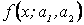 , то для отыскания оценок параметров
, то для отыскания оценок параметров  необходимо иметь уже два уравнения относительно этих параметров. Для этого можно воспользоваться, например, первым начальным моментом (математическим ожиданием) и вторым центральным (дисперсией).
необходимо иметь уже два уравнения относительно этих параметров. Для этого можно воспользоваться, например, первым начальным моментом (математическим ожиданием) и вторым центральным (дисперсией).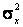 нормального распределения:
нормального распределения: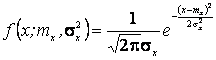 .
.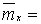
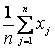 ,
, 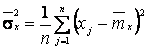 .
.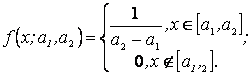
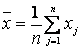 ,
, 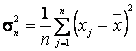 ,(
,(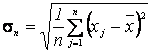 ) (8.2)
) (8.2)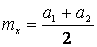 ,
, 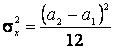 .
.
 ,
, 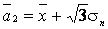 ,
,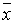 ,
, 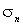 определены соотношениями (2).
определены соотношениями (2).