
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точечные и интервальные оценки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Точечной оценкой неизвестного параметра называют число (точку на числовой оси), которое приблизительно равно оцениваемому параметру и может заменить его с достаточной степенью точности в статистических расчетах. Для того чтобы точечные статистические оценки обеспечивали “хорошие” приближения неизвестных параметров, они должны быть несмещенными, состоятельными и эффективными. Определение:Пусть Формально статистика Свойства точечных оценок Оценка
где Оценка Оценка
Оценка
Надо отметить, что проверить на опыте сходимость «почти наверное» не представляется возможным, поэтому с точки зрения прикладной статистики имеет смысл говорить только о сходимости по вероятности. Интервальной называют оценку, которая определяется двумя числами – концами отрезка. Интервальные оценки – характеризуют не единственно возможную ситуацию, а их множественность. Этот вид экспертных оценок широко распространен. Одним из определяющих свойств интервальной оценки является то, что на множестве задано бинарное отношение МЕЖДУ. Определение Пусть
Интервал Примеры интервальных оценок Пример 1. Доверительное оценивание по вариационному ряду. Пусть задана выборка
Очевидно, что вероятность попасть в любой из
Вопрос: чему должен быть равен размер выборки n чтобы вероятность попасть в интервал Подставляя значение для доверительной вероятности в формулу выше, получим:
откуда Таким образом, при достаточном для заданной доверительной вероятности числе измерений случайной величины Пример 2. Доверительный интервал для медианы. Пусть задана выборка При
где
Для значений Пример 3. Доверительный интервал для математического ожидания. Пусть задана выборка
Величину Найдем такую величину Например, выбирая Окончательно: с вероятностью
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 784; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.153.240 (0.009 с.) |

 — случайная выборка из распределения, зависящего от параметра
— случайная выборка из распределения, зависящего от параметра  . Тогда статистику
. Тогда статистику  , принимающую значения в
, принимающую значения в  , называют точечной оценкой параметра
, называют точечной оценкой параметра  Замечание
Замечание может не иметь ничего общего с интересующим нас значением параметра
может не иметь ничего общего с интересующим нас значением параметра  называется несмещённой, если её математическое ожидание равно оцениваемому параметру генеральной совокупности:
называется несмещённой, если её математическое ожидание равно оцениваемому параметру генеральной совокупности: ,
, обозначает математическое ожидание в предположении, что
обозначает математическое ожидание в предположении, что  ).
). называется состоятельной, если она по вероятности с увеличением объема выборки n стремится к параметру генеральной совокупности:
называется состоятельной, если она по вероятности с увеличением объема выборки n стремится к параметру генеральной совокупности: 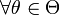 ,
,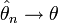 по вероятности при
по вероятности при  .
. называется сильно состоятельной, если
называется сильно состоятельной, если  - неизвестный параметр генеральной совокупности. По сделанной выборке по определенным правилам находятся числа
- неизвестный параметр генеральной совокупности. По сделанной выборке по определенным правилам находятся числа  и
и  такие чтобы выполнялось неравенство:
такие чтобы выполнялось неравенство:
 является доверительным интервалом для параметра
является доверительным интервалом для параметра  - доверительной вероятностью или надежностью сделанной оценки. Обычно надежность задается заранее, причем выбираются числа близкие к 1 (0.95, 0.99 или 0.999).
- доверительной вероятностью или надежностью сделанной оценки. Обычно надежность задается заранее, причем выбираются числа близкие к 1 (0.95, 0.99 или 0.999). некоторой случайной величины
некоторой случайной величины  Построим вариационный ряд выборки
Построим вариационный ряд выборки 

 - го интервалов значений случайной величины X одинакова и равна
- го интервалов значений случайной величины X одинакова и равна  Тогда вероятность того, что случайная величина X приняла значение из интервала
Тогда вероятность того, что случайная величина X приняла значение из интервала  где
где  будет равна:
будет равна:
 составила 95%.
составила 95%.

 по набору ее порядковых статистикможет быть оценен диапазон принимаемых ею значений.
по набору ее порядковых статистикможет быть оценен диапазон принимаемых ею значений. доверительный интервал для медианы
доверительный интервал для медианы  определяется порядковыми статистиками
определяется порядковыми статистиками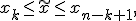
 при
при 
 при
при 
 при
при 
 номера порядковых статистик, заключающих в себе медиану, при
номера порядковых статистик, заключающих в себе медиану, при  и
и  приведены в таблице 1, взятой из [3].
приведены в таблице 1, взятой из [3].
 - несмещенная оценка дисперсии.
- несмещенная оценка дисперсии. называют оценкой среднего квадратического отклонения. Воспользуемся тем, что величина
называют оценкой среднего квадратического отклонения. Воспользуемся тем, что величина  представляет собой сумму
представляет собой сумму  независимых случайных величин, и, согласно центральной предельной теореме, при достаточно большом
независимых случайных величин, и, согласно центральной предельной теореме, при достаточно большом  .
. , для которой
, для которой  . Перепишем это в эквивалентном виде
. Перепишем это в эквивалентном виде  и скажем, что случайная величина перед знаком неравенства есть модуль от стандартной нормальной. Получаем, что
и скажем, что случайная величина перед знаком неравенства есть модуль от стандартной нормальной. Получаем, что  , и
, и  . В случае неизвестной дисперсии ее можно заменить на оценку
. В случае неизвестной дисперсии ее можно заменить на оценку  .
.
 можно сказать, что
можно сказать, что 



