
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики дискретных случайных величинСодержание книги
Поиск на нашем сайте
Закон распределения полностью характеризует дискретную случайную величину. Однако, когда невозможно определить закон распределения, или этого не требуется, можно ограничиться нахождением значений, называемых числовыми характеристиками случайной величины: Математическое ожидание, Дисперсия, Среднее квадратичное отклонение Эти величины определяют некоторое среднее значение, вокруг которого группируются значения случайной величины, и степень их разбросанности вокруг этого среднего значения. Математическое ожидание M дискретной случайной величины - это среднее значение случайной величины, равное сумме произведений всех возможных значений случайной величины на их вероятности.
Плотность распределения вероятностей НСВ. Вероятность попадания НСВ. Свойства плотности распределения. Числовые характеристики НСВ. Определение и свойства функции распределения сохраняются и для непрерывной случайной величины, для которой функцию распределения можно считать одним из видов задания закона распределения. Но для непрерывной случайной величины вероятность каждого отдельного ее значения равна 0. Это следует из свойства 4 функции распределения: р(Х = а) = F(a) — F(a) = 0. Поэтому для такой случайной величины имеет смысл говорить только о вероятности ее попадания в некоторый интервал. Вторым способом задания закона распределения непрерывной случайной величины является так называемая плотность распределения (плотность вероятности, дифференциальная функция). Определение 5.1. Функция f(x), называемая плотностью распределения непрерывной случайной величины, определяется по формуле: f (x) = F′(x), то есть является производной функции распределения. Свойства плотности распределения. 1) f(x) ≥ 0, так как функция распределения является неубывающей. 2), что следует из определения плотности распределения. 3) Вероятность попадания случайной величины в интервал (а, b) определяется формулой Действительно, 4) (условие нормировки). Его справедливость следует из того, что а 5) так как при Таким образом, график плотности распределения представляет собой кривую, располо-женную выше оси Ох, причем эта ось является ее горизонтальной асимптотой при (последнее справедливо только для случайных величин, множеством возможных значений которых является все множество действительных чисел). Площадь криволинейной трапеции, ограниченной графиком этой функции, равна единице. Замечание. Если все возможные значения непрерывной случайной величины сосредоточе-ны на интервале [a, b], то все интегралы вычисляются в этих пределах, а вне интервала [a, b] f(x) ≡ 0.
Нормальное распределение. Нормальный закон распр-я н.с.в. – закон, который хар-ся след.пл-тью распр-я.
Q= D(Х) под корнем = Q (Х), → параметр a = мат. ожид-ю, а пар. Q = среднему квадратич. О откл- ю нормально распр-ой с.в.х.
|
||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 378; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.86 (0.006 с.) |

 → норм-ый закон опред-ся двумя параметрами а и (жигма)
→ норм-ый закон опред-ся двумя параметрами а и (жигма)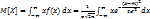 = а
= а = Q₂
= Q₂


