
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные характеристики случайных процессовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Случайными (стохастическими) процессами являются внешние помехи, флуктуационные шумы на выходе дискриминатора и других устройств РАС, внутренние возмущения в РАС: нестабильность частоты ПГ, нестабильность устройств регулируемой временной задержки и др. Исследование РАС при случайных воздействиях в принципе можно проводить обычными методами, определяя параметры качества РАС при самых неблагоприятных (максимальных) значениях возмущения (наихудший случай). Однако, поскольку максимальное значение случайной величины маловероятно и будет наблюдаться редко, к РАС будут предъявляться заведомо жесткие требования. Более рациональные решения можно получить, рассматривая наиболее вероятное значение случайной величины. Закон распределения флуктуационных составляющих в линейных РАС можно считать нормальным (Гауссовским). Нормальный закон распределения характерен для внутренних возмущений. При прохождении случайного процесса через линейную систему, нормальный закон распределения остается неизменным. Если на входе РАС или в любой другой точке (например, на выходе дискриминатора) присутствует возмущение с законом распределения, отличным от нормального, и обладающее широким спектром S (ω), это возмущение эффективно нормализуется узкополосными элементами фильтра РАС. Случайный процесс с нормальным законом распределения полностью определяется математическим ожиданием m (t) и корреляционной функцией R (τ). Математическое ожидание (матожидание) случайного процесса x (t) представляет собой некоторую регулярную функцию mx (t), около которой группируются все реализации данного процесса ( mx (t) = М { x (t)} = Случайный процесс Для учета степени разбросанности [10] случайного процесса относительно его среднего значения mx (t) вводят понятие дисперсии: Dx (t) = М {( Среднее значение квадрата случайного процесса связано с его матожиданием mx (t) и дисперсией Dx (t) формулой: На практике удобно оценивать случайный процесс статистическими характеристиками хскв (t) и s x (t), имеющими ту же размерность, что и сам процесс. Среднеквадратичное значение хскв (t) случайного процесса:
Среднеквадратичное отклонение хскв(t) случайного процесса:
Матожидание и дисперсия не дают достаточного представления о характере отдельных реализаций случайного процесса. Для того, чтобы учесть степень изменчивости процесса или связь между его значениями в различные моменты времени, вводится понятие корреляционной (автокорреляционной) функции. Корреляционная функция центрированного процесса
где Корреляционная функция является четной: R (τ) = R (– τ). Если функции распределения и плотности вероятности процесса не зависят от сдвига по времени на одинаковую величину всех временных аргументов, такой случайный процесс называют стационарным. Если у стационарного процесса совпадают значения среднего по множеству и среднего по времени, такой случайный процесс называют эргодическим. Зная R (τ) можно определить дисперсию стационарного процесса:
Спектральная плотность S l y (ω) выходного процесса y (t) в линейной системе и спектральная плотность S l(ω) входного воздействия связаны соотношением:
Корреляционная функция R (τ) стационарного случайного процесса и его спектральная плотность S (ω) связаны преобразованием Фурье, поэтому часто анализ проводят в частотной области. Выполнив преобразование Фурье для (6.7), получаем выражение для корреляционной функции выходного процесса Ry (τ):
Спектральные плотности S l y (ω) и S l(ω)являются двусторонними. Можно ввести одностороннюю спектральную плотность N (f), которая определяется только для положительных частот ( С учетом четности R (τ) и формулы Эйлера (6.8) можно упростить:
Качество работы РАС относительно случайных сигналов и помех характеризуется суммарной среднеквадратической ошибкой (СКО). Рассмотрим обобщенную РАС, схема которой представлена на рис. 2.11. Считаем воздействие λ(t) детерминированным, а возмущение ξ(t) на выходе дискриминатора – случайным процессом. С помощью формул (2.28)–(2.31) определим ПФ для ошибки при воздействии и возмущении.
В общем случае между процессами воздействия и возмущения может существовать корреляция (связь). В этом случае кроме автокорреляционных функций вида (6.8) для каждого из процессов необходимо учитывать взаимные корреляционные функции процессов относительно друг друга. Через спектральные плотности по ошибке данные связи записывается следующим образом:
После подстановки выражения (6.11) в формулу (6.8) получим соответствующие составляющие дисперсии:
Если корреляция между процессами отсутствует, то S lx(ω) = S xl(ω) = 0, а также D lx = D xl = 0, и формула (6.12) упрощается
Матожидание ошибки х (t) находится аналогично определению в установившемся режиме: Если спектральная плотность Sх (ω) описывается дробно-рациональной функцией относительно ω, то для вычисления Dx его представляют в виде:
где Интегралы (6.14) можно вычислить по формуле (6.15) [10]:
где D n – старший определитель Гурвица вида (4.7), составленный из коэффициентов аj, а Qn – определитель вида D n, в котором в первой строке коэффициенты аj заменены на bj. Для интеграла (6.15) есть таблицы значений [1–5, 10] для n ≤ 7. Значения при n ≤ 4 определяются по формулам:
Пример 6.1. Определим СКО системы ФАПЧ из примера 4.2. Пусть на входе РАС действует сигнал λ(t) = 1 + 0,1 t, а возмущение ξ(t) представляет собой белый шум с амплитудой N0 = 1 мВ ( Коэффициенты ошибок для данной РАС уже были найдены в примере 5.1. Из формул (5.19)–(5.22) получаем Для ПФ ошибки по возмущению из формулы (2.30) после замены переменных р ® i ω получим (К1 = Sд, k 0 = k 1 Sд, k 1 = kфkи):
После подстановки формулы (6.17) в (6.13) (D l = 0) получим:
Сравнивая (6.18) с выражением (6.14), находим порядок и коэффициенты полиномов (6.14): n = 3, b2 = 0, b1 = –(T2)2, b0 = 1; a3 = TфTд, a2 = Tф + Tд, a1 = 1 + k 0 T2, a0 = k 0. После подстановки в формулу (6.16) и преобразований получим:
После подстановки численных значений в результате получаем: mx = 5×10–4 (1/с), Dx = 1,06×10–3 (1/с2) (при k 0 = 200, Sд = 10, k 1 = 20) или mx = 5×10–4 (1/с), Dx = 0,66 (1/с2) (при k 0 = 200, Sд = 0,4, k 1 = 500). Из (6.3), (6.4) следует, что xско ≈ s x = 0,032 (1/с) при Sд = 10, а при Sд = 0,4 xско ≈ s x = 0,81 (1/с).
Пример 6.2. Определим СКО РАС из примера 4.5 при тех же сигналах: λ(t) = 1 + 0,1 t и ξ(t) = N0 = 1 мВ. λ′(t) = λ1, λ″(t) = 0
Коэффициенты ошибок для данной РАС найдем по формуле (5.19):. v = 0, d1 = 0, d0 = Sд, b3 = Т1Т2Т3, b2 = Т1Т2 + Т2Т3 + Т1Т3, b1 = Т1+Т2+Т3, b0 = 1. Из формул (5.19)–(5.22) получаем
Для ПФ ошибки по возмущению из формулы (2.30) после замены переменных р ® i ω в (6.20) получим:
После подстановки формулы (6.20) в (6.13) (Dl = 0) получим:
Сравнивая (6.21) с выражением (6.14), находим коэффициенты полиномов (6.14): n = 3, b2 = b1 = 0, b0 = 1; a3 = Т1Т2Т3, a2 = Т1Т2 + Т2Т3 + Т1Т3, a1 = Т1+Т2+Т3, a0 = Sд + 1. После подстановки в формулу (6.16) и преобразований получим:
После подстановки численных значений получаем в результате: mx = (9,2 + 0,9 t)10–2, Dx = 4,2×10–4. 6.2. Графоаналитический метод определения дисперсии.
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 2601; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.72.24 (0.012 с.) |

 – плотность вероятности) [10]. Его называют также средним значением по множеству (ансамблю).
– плотность вероятности) [10]. Его называют также средним значением по множеству (ансамблю).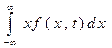 . (6.1)
. (6.1) (t) без регулярной составляющей mx (t) называется центрированным
(t) без регулярной составляющей mx (t) называется центрированным  .
. . (6.2)
. (6.2) .
. . (6.3)
. (6.3) . (6.4)
. (6.4) , (6.5)
, (6.5) – двумерная плотность вероятности.
– двумерная плотность вероятности. . (6.6)
. (6.6) . (6.7)
. (6.7) . (6.8)
. (6.8) ).
). . (6.9)
. (6.9) . (6.10)
. (6.10)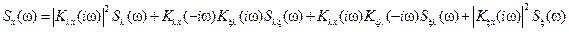 . (6.11)
. (6.11) . (6.12)
. (6.12) . (6.13)
. (6.13) .
. . (6.14)
. (6.14)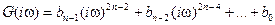 – полином, содержащий четные степени i ω до 2 n –2 включительно; а
– полином, содержащий четные степени i ω до 2 n –2 включительно; а  – полином степени n, корни которого лежат в верхней полуплоскости комплексной переменной ω.
– полином степени n, корни которого лежат в верхней полуплоскости комплексной переменной ω. , (6.15)
, (6.15)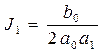 ,
,  ,
,  ,
, . (6.16)
. (6.16) ).
). .
. , (6.17)
, (6.17) . (6.18)
. (6.18) . (6.19)
. (6.19)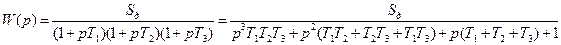 . (6.20)
. (6.20) .
. , (6.21)
, (6.21) . (6.22)
. (6.22) . (6.23)
. (6.23)


