
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности работы нелинейной системы чапСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Структурная схема ЧАП с преобразованием частоты приведена на рис. 3.3 и описана в линейном режиме в параграфе 3.2. Построим структурную схему ЧАП (рис. 8.3) с учетом нелинейности характеристики дискриминатора F(Ω) (рис. 3.4).
 
В анализе примем, что нестабильностью частоты ГУН можно пренебречь. Примем, что Составим уравнение работы ЧАП относительно отклонения частоты.
Будем считать, что ЧАП работает в режиме стабилизации частоты (сигналом воздействия является частота эталонного генератора wэт).
Решим уравнение (8.4) для стационарного режима (t ® ¥ или p ® 0). В этом случае
Правая часть (8.5) представляет собой уравнение прямой относительно переменной W. Решением будут являться точки пересечения (точки 1, 2, 3 на рис. 8.4) этой прямой и графика дискриминационной характеристики F(Ω). Полученные решения Ω 1, Ω 2, Ω 3 для общего случая (сплошная прямая a на рис. 8.4) необходимо проанализировать на локальную устойчивость. Есть несколько способов. Воспользуемся простейшим [2]: линеаризацией характеристики в области каждой точки решения (
Подстановка (8.6) в (8.4) после замены переменных дает
Решение (8.7) и анализ устойчивости [2] приводят к следующим условиям устойчивости решений:
В точке 1 крутизна характеристики Sд1 > 0 и условие устойчивости (8.8) выполняется. В точке 2 Sд2 < 0 и Система не может находиться в точке 2, она должна перейти в устойчивое состояние – точку 1 или 3. В зависимости от начальной расстройки Δω c (возможные изменения показаны стрелочками на рис. 8.4) уравнение (8.5) может иметь одно или два решения. Двум решениям на рис. 8.4 соответствуют штриховые линии: b и c. Штриховая линия b позволяет определить по точке пересечения с осью абсцисс полосу захвата (при этом точки 1 и 2 сливаются), а штриховая линия c – полосу удержания (при этом сливаются точки 2 и 3)) [24]. Рабочая полоса ЧАП – полоса захвата (точки 1 на рис. 8.4). Полоса удержания не может быть меньше, чем полоса захвата. Одному решению, которое получается при нахождении начальной расстройки в полосе захвата, на рис. 8.4 соответствует штрихпунктирная линия d [24]. Зависимость остаточной расстройки Ω от начальной Δωс называется регулировочной характеристикой и является наиболее информативной характеристикой ЧАП (рис. 8.5) (kап = 1 + Sд kф kр). Система ЧАП является статической РАС с конечной ошибкой Пусть при включении ЧАП находится в асинхронном режиме, в этом случае начальная расстройка Δωс находится вне полосы удержания (Δω с > ω уд), частота ГУН равна некоторой собственной частоте (частота при разомкнутой петле ОС). При медленном изменении частоты эталонного генератора в сторону уменьшения рассогласования частот, как только расстройка Δω с окажется в полосе захвата (Δω с < ω зх ), ЧАП войдет в режим слежения (синхронизм, рабочий режим) за частотой сигнала (в режиме стабилизации – за частотой эталонного генератора). При этом частота ГУН меняется скачком и ее отличие от ω э уменьшается в kап раз, в результате частота ГУН почти равна частоте эталонного генератора.
Если теперь начать увеличивать расстройку Δω с, ЧАП будет работать в синхронном режиме до тех пор, пока значение расстройки будет оставаться внутри полосы удержания (Δω с < ω уд). Чтобы вывести ЧАП из синхронного режима потребуется увеличить расстройку так, чтобы она оказалась вне полосы удержания (Δω с > ω уд). Если при включении ЧАП начальная расстройка окажется в полосе захвата (Δω с < ω зх), то система сразу входит в синхронизм. Если при включении ЧАП начальная расстройка будет лежать в интервале между полосой захвата и удержания (ω зх < Δω с < ω уд), то достоверно поведение предсказать нельзя, так как система перейдет в одно из рассмотренных ранее устойчивых состояний. Максимальная корректирующая расстройка Δω k max, вырабатываемая системой ЧАП, соответствует точке (1 = 2) на рис. 8.4 и равна Δω k max = kрSдUд max, (8.9) где U д max – максимальное напряжение на выходе дискриминатора. Соотношение между полосой захвата и удержания оценивается следующими формулами:
Точность системы прямопропорциональна kап , поэтому для уменьшения установившейся ошибки kап следует увеличивать. Однако при этом, как следует из формул (8.10), уменьшается полоса захвата, а значит, уменьшается рабочий диапазон частот эффективной автоподстройки. Таким образом, в статической ЧАП есть противоречие между точностью и полосой эффективной автоподстройки. Для разрешения данного противоречия используют астатическую ЧАП.
На рис. 8.6. приведена ПХ для этого случая. Время регулирования оценивается формулой Применение системы ЧАП в РПрмУ по сравнению с ФАПЧ имеет достоинство: ЧАП не реагирует на «зеркальную помеху». Нелинейная система ФАПЧ Структурная схема ФАПЧ приведена на рис. 3.6, а на рис. 3.7 приведена ее схема, сведенная к обобщенному виду. Работа линеаризованной системы ФАПЧ в режиме стабилизации частоты описана в параграфе 3.3. Проанализируем работу ФАПЧ в режиме стабилизации частоты с учетом нелинейности дискриминационной характеристики. Будем считать, что начальная фаза опорного (эталонного) генератора φ 0 = 0, возмущение x(t) отсутствует, а нестабильностью частоты эталонного генератора и ГУН можно пренебречь. Принципиальным отличием статической характеристики ФД является ее периодичность. Для непрерывных (аналоговых) систем ФАПЧ статическая характеристика представляет собой «синусоиду». В импульсных и цифровых системах характеристика ФД имеет другие формы. ФД выполняет перемножение сигналов эталонного генератора ГУН. За основу примем уравнения ФАПЧ (3.7) и (3.8).
Пусть Кг (р) = 1, Кр (р) = kр ;
Рассмотрим сначала работу системы ФАПЧ при отсутствии фильтра (Кф (р) = 1). В этом случае уравнение (8.12) преобразуется к виду
где
На рис. 8.7 показано графическое решение уравнения (8.14). Считаем, что Анализ полученных решений на устойчивость, приведенный в [2, 24], показывает, что точки пересечения с графиком F н (j), которые находятся на участках с
Точка 1 находится на участке (j < ±0,5p), который приближенно считается линейным в линеаризованной системе ФАПЧ (п. 3.3). На рис. 8.8 приведена регулировочная характеристика (зависимость остаточной расстройки от начальной) для ФАПЧ при отсутствии фильтра. В отличие от ЧАП, регулировочная характеристика ФАПЧ имеет область (полоса удержания 2ωуд), в которой установившаяся ошибка равна нулю. Таким образом, система ФАПЧ является астатической по частоте, а по фазе имеет некоторый постоянный фазовый сдвиг.
При отсутствии фильтра полосы захвата и удержания совпадают. Если расстройка Δω находится в полосе удержания, то ФАПЧ находится в режиме синхронизма, в котором частота ГУН устанавливается равной частоте эталонного генератора (ω г = ω э) с точностью до фазы. Если увеличивать начальную расстройку Δω так, чтобы она вышла из полосы удержания, то ФАПЧ перейдет в режим биений. В режиме биений напряжение на выходе дискриминатора не постоянно, а периодически изменяется; фаза сигнала неограниченно нарастает, частота ГУН периодически колеблется вокруг частоты сигнала. Положительные и отрицательные полуволны периода имеют разную длительность, поэтому кроме переменной составляющей на выходе ФД появляется и постоянная составляющая. Для возвращения ФАПЧ в рабочий режим необходимо уменьшить расстройку Δω так, чтобы она вернулась в полосу удержания. По мере уменьшения Δω будет увеличиваться доля постоянной составляющей на выходе ФД и уменьшаться частота биений. При вхождении ФАПЧ в синхронизм ФД будет иметь только постоянную составляющую, величина и полярность которой будут зависеть от величины и знака начальной расстройки. Проанализируем теперь работу ФАПЧ с ФНЧ первого порядка (например, интегрирующая RC -цепь
где Получилось уравнение второго порядка, которое удобно свести к стандартному виду:
где Уравнение ФАПЧ (8.12) в данном случае запишется в виде.
После преобразований получим:
На рис. 8.9 приведена типичная регулировочная характеристика для данного случая. При малой постоянной времени фильтра Тф (это эквивалентно его широкой полосе пропускания) полоса захвата ω зх имеет почти тот же размер, что и полоса удержания ω уд. С увеличением постоянной времени Тф улучшаются фильтрирующие свойства системы по отношению к сигналу, но в то же время уменьшается полоса захвата системы. Уменьшение полосы захвата можно объяснить так. При существенной начальной расстройке на выходе ФД существуют колебания с частотой начальной расстройки, которые ослабляются ФНЧ. В результате максимально возможное напряжение на входе ГУН получается меньше, чем в рассмотренном выше случае, в котором ФНЧ отсутствовал [24]. При значительных постоянных времени ФНЧ (
Кроме того, при выборе Тф следует учитывать характер (z) и время регулирования переходного процесса РАС. Для уменьшения данного противоречия необходимо скорректировать характеристики фильтра. Наиболее простое решение – применение пропорционально-интегрирующего фильтра (ПИФ).
На рис. 8.10 представлены возможные схемы ПИФ. ПФ ПИФ определяется формулой
где Тф = (R1 + R2) C1, a = R1 /(R1 + R2)для схемы а), а для схемы б) Тф = R1 (C1 + C 2), a = C1 (C1 + C 2).
На рис. 8.11 представлена регулировочная характеристика для системы ФАПЧ с ПИФ. Штриховыми стрелочками на рис. 8.11 для сравнения показана полоса захвата при использовании интегрирующего RC -фильтра, рассмотренного выше. Введение ПИФ обеспечивает увеличение запаса РАС по фазе.
Рассмотрим работу нелинейной ФАПЧ при различных величинах начальной расстройки Δω. Пусть при включении начальная расстройка Δω находится в полосе захвата, в этом случае ФАПЧ находится в синхронном режиме, в котором частота ГУН устанавливается равной частоте эталонного генератора с точностью до фазы. Если увеличивать начальную расстройку Δω так, чтобы она вышла из полосы удержания, то ФАПЧ прекратит нормальную работу и перейдет в режим биений [24]. Для возвращения ФАПЧ в рабочий режим необходимо уменьшить расстройку Δω так, чтобы она вернулась в полосу захвата. По мере уменьшения Δω будет увеличиваться доля постоянной составляющей на выходе ФД и уменьшаться частота биений. Если при включении ФАПЧ в синхронизм ФД расстройка Δω будет находиться вне полосы захвата, но в полосе удержания (ω зх < Δω < ω уд ), то достоверно поведение ФАПЧ предсказать нельзя: она может перейти как в синхронный, так и в асинхронный режимы.
Так как системы ЧАП и ФАПЧ имеют свои достоинства и недостатки, представляет интерес применение комбинированных РАС, в которых за счет объединения работы ФАПЧ и ЧАП удается получить существенное улучшение качества работы [24].
|
||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1846; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 ;
;  ; W – отклонение частоты на выходе ЧАП (частота ГУН, промежуточная частота) в установившемся режиме от номинального значения (остаточная расстройка).
; W – отклонение частоты на выходе ЧАП (частота ГУН, промежуточная частота) в установившемся режиме от номинального значения (остаточная расстройка). . (8.2)
. (8.2) . (8.3)
. (8.3) . (8.4)
. (8.4) и уравнение сводится к виду (8.5).
и уравнение сводится к виду (8.5). . (8.5)
. (8.5) Для наглядности решим уравнение (8.5) графически.
Для наглядности решим уравнение (8.5) графически. ).
).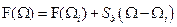 . (8.6)
. (8.6) :
: . (8.7)
. (8.7) . (8.8)
. (8.8) – условие (8.8) не выполняется, и система неустойчива. В точке 3 Sд3 < 0, но
– условие (8.8) не выполняется, и система неустойчива. В точке 3 Sд3 < 0, но  , поэтому условие (8.8) выполняется, и система устойчива.
, поэтому условие (8.8) выполняется, и система устойчива. (kап = 1 + Sд kф kр – коэффициент автоподстройки).
(kап = 1 + Sд kф kр – коэффициент автоподстройки).
 ;
;  ;
;  . (8.10)
. (8.10) В переходном режиме поведение ошибки будет зависеть в основном от характеристики фильтра. Для данного случая
В переходном режиме поведение ошибки будет зависеть в основном от характеристики фильтра. Для данного случая 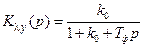 , и остаточная расстройка будет изменяться не скачком, а плавно с некоторой задержкой.
, и остаточная расстройка будет изменяться не скачком, а плавно с некоторой задержкой. .
. . (8.11)
. (8.11) – нормированная характеристика дискриминатора.
– нормированная характеристика дискриминатора. . (8.12)
. (8.12) , (8.13)
, (8.13) – максимальная корректирующая расстройка, которая в данном случае имеет смысл полосы удержания ω уд.
– максимальная корректирующая расстройка, которая в данном случае имеет смысл полосы удержания ω уд. Если рассмотреть стационарный режим, то приходим к уравнению статики:
Если рассмотреть стационарный режим, то приходим к уравнению статики: , (8.14)
, (8.14) . Штриховая прямая
. Штриховая прямая  пересекает график F н (j) в двух точках на периоде.
пересекает график F н (j) в двух точках на периоде. соответствуют устойчивому состоянию (точки 1 и 3), а точки, находящиеся на участках с отрицательной крутизной дискриминационной характеристики
соответствуют устойчивому состоянию (точки 1 и 3), а точки, находящиеся на участках с отрицательной крутизной дискриминационной характеристики  , – неустойчивому состоянию (точки 2 и 4).
, – неустойчивому состоянию (точки 2 и 4). Штрихпунктирная прямая на рис. 8.7 (точки 1 и 2, а также 3 и 4 сливаются) соответствует пределам рабочего участка (j = ±0,5p + p n), который определяет полосу захвата ФАПЧ.
Штрихпунктирная прямая на рис. 8.7 (точки 1 и 2, а также 3 и 4 сливаются) соответствует пределам рабочего участка (j = ±0,5p + p n), который определяет полосу захвата ФАПЧ. . (
. ( ) (8.15)
) (8.15) из прил. 2).
из прил. 2). , (8.16)
, (8.16) .
. , (8.17)
, (8.17) ,
,  .
. . (8.18)
. (8.18)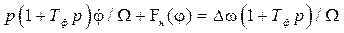 ,
,
 . (8.19)
. (8.19) ) отношение полос захвата и удержания оценивается формулой [24].
) отношение полос захвата и удержания оценивается формулой [24]. ,
,  . (8.20)
. (8.20)
 , (8.21)
, (8.21)



