
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметры системы. Фазовая траектория. Фазовое пространствоСодержание книги
Поиск на нашем сайте Пусть T = [t0, t1] есть временной интервал моделирования системы S (интервал модельного времени). Построение модели начинается с определения параметров и переменных, определяющих процесс функционирования системы. Параметры системы Переменные бывают зависимые и независимые. Независимые переменные есть, как правило, входные воздействия (в том числе управляющие)
ими могут быть также воздействия внешней среды. Последовательность изменения x(t) при
называется фазовой траекторией системы, Последовательность изменения y(t) называется выходной траекторией системы. Зависимые переменные есть выходные характеристики (сигналы) Математическая модель системы Общая схема математической модели (ММ) функционирования системы может быть представлена в виде:
Множество переменных
называется математической моделью системы. Если t непрерывно, то модель называется непрерывной, иначе – дискретной:
Если модель не содержит случайных элементов, то она называется детерминированной, в противном случае – вероятностной, стохастической. Если математическое описание модели слишком сложное и частично или полностью неопределенно, то в этом случае используются агрегативные модели. Сущность агрегативной модели заключается в разбиении системы на конечное число взаимосвязанных частей (подсистем), каждая из которых допускает стандартное математическое описание. Эти подсистемы называются агрегатами. Имитация случайных величин и процессов. Базовый датчик Моделирование случайных элементов в системах является одной из самых базовых задач математического моделирования. Любая случайная величина или процесс X может моделироваться следующим образом:
Базовый датчик выдает независимые равномерно распределенные случайные величины: непрерывные в (0,1); дискретные в Типы базовых датчиков: ‑ физические (любой физический шум), в последнее время практически не используются, т.к. характеристики нестабильны и реализацию повторить нельзя; ‑ псевдослучайные датчики строятся на основе детерминированного алгоритма, но полученные результаты мало отличны от случайных. Псевдослучайные базовые датчики строятся по модели
при заданном x0. Рассмотрим формулу получения случайных чисел Хn+1 = (a Хn + c) mod m, n ³ 0, характерную для линейной конгруэнтной последовательности случайных чисел, где m — модуль, m > 0; a — множитель, 0 £ a < m; c — приращение, 0 £ с < m; Х0 — начальное значение, 0 £ Х0 < m.
Пусть m = 16; Х0 =9; a = c = 5, тогда воспользовавшись последней формулой, получим последовательность 9, 2, 15, 0, 5, 14, 11, 12, 1,10,7,8,13,6,3,4,9…
Требования к базовым датчикам: Отрезок апериодичности. Равномерность. Некоррелированность. Основы математического моделирования. Линеаризация Отметим основные операции математического моделирования: Линеаризация. Пусть дана математическая модель
М=М(X, Y, A),
где X - множество входов, Y - множество выходов, А - множество состояний системы. Схематически можно это изобразить так: X
Если X, Y, A - линейные пространства (множества), а
- линейные операторы, которые любые линейные комбинации ax + by преобразуют в линейные комбинации типа A* то система (модель) называется линейной. Все другие системы (модели) - нелинейные. Они труднее поддаются исследованию, хотя и более актуальны. Нелинейные модели менее изучены, поэтому их часто линеаризуют - сводят к линейным моделям. Например, применим операцию линеаризации по Тейлору в точке t0 = 2 к процессу: У(t) = bt2/2, 0 функция является нелинейной (квадратичной). Процедура линеаризации даст линейную модель вида y = -2b+2bt. Чтобы понять ответ, вспомним положение о разложении аналитической функции в ряд Тейлора. Пусть f(t) - действительная непрерывная функция, имеющая в интервале с <= t < b n – ю производную. Тогда
где Rn(t) – остаточный член разложения, а
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 345; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.006 с.) |

 -это характеристики системы, остающиеся постоянными на всем интервале T.
-это характеристики системы, остающиеся постоянными на всем интервале T.

 , где X – пространство состояний или фазовое пространство.
, где X – пространство состояний или фазовое пространство.

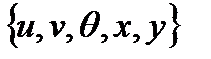 вместе с законами функционирования
вместе с законами функционирования
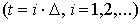 .
.
 .
.

 A
A  и
и 
 t
t 
 - производные i - го порядка функции f(t) в точке разложения
- производные i - го порядка функции f(t) в точке разложения  . Ответ получен в точке
. Ответ получен в точке 


