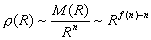Статические и динамические, дискретные и непрерывные модели

Статические и динамические, дискретные и непрерывные модели

Классификацию моделей проводят по различным критериям.

Модель называется статической, если среди параметров, участвующих в ее описании, нет временного параметра. Статическая модель в каждый момент времени дает лишь "фотографию" системы, ее срез.

Пример. Закон Ньютона F=a*m - это статическая модель движущейся с ускорением a материальной точки массой m. Эта модель не учитывает изменение ускорения от одной точки к другой.

Модель динамическая, если среди ее параметров есть временной параметр, т.е. она отображает систему (процессы в системе) во времени.

Пример. Динамическая модель закона Ньютона будет иметь вид:

F(t)=a(t)*m(t).

Модель дискретная, если она описывает поведение системы только в дискретные моменты времени.

Пример. Если рассматривать только t=0, 1, 2, …, 10 (сек), то модель

St=gt2/2

или числовая последовательность: S0=0, S1=g/2, S2=2g, S3=9g/2,:, S10=50g может служить дискретной моделью движения свободно падающего тела.

Модель непрерывная, если она описывает поведение системы для всех моментов времени некоторого промежутка времени.

Пример. Модель S=gt2/2, 0 < t < 100 непрерывна на промежутке времени (0;100).

Модель имитационная, если она предназначена для испытания или изучения возможных путей развития и поведения объекта путем варьирования некоторых или всех параметров модели.

Пример. Пусть модель экономической системы производства товаров двух видов 1 и 2, в количестве x1 и x2 единиц и стоимостью каждой единицы товара a1 и a2 на предприятии описана в виде соотношения:

a1x1 + a2x2 = S,

где S - общая стоимость произведенной предприятием всей продукции (вида 1 и 2). Можно ее использовать в качестве имитационной модели, по которой можно определять (варьировать) общую стоимость S в зависимости от тех или иных значений объемов и стоимости производимых товаров.

Детерминированные и стохастические модели

Модель детерминированная, если каждому входному набору параметров соответствует вполне определенный и однозначно определяемый набор выходных параметров; в противном случае - модель недетерминированная, стохастическая (вероятностная).

Пример. Приведенные выше физические модели - детерминированные. Если в модели S = gt2 / 2, 0 < t < 100 мы учли бы случайный параметр - порыв ветра с силой p при падении тела:

S(p) = g(p) t2 / 2, 0 < t < 100,

то мы получили бы стохастическую модель (уже не свободного) падения.

Функциональные, теоретико-множественные и логические модели

Модель функциональная, если она представима в виде системы каких- либо функциональных соотношений.

Модель теоретико-множественная, если она представима с помощью некоторых множеств и отношений принадлежности им и между ними.

Пример. Пусть задано множество

X = {Николай, Петр, Николаев, Петров, Елена, Екатерина, Михаил, Татьяна} и отношения:

Николай - супруг Елены,

Екатерина - супруга Петра,

Татьяна - дочь Николая и Елены,

Михаил - сын Петра и Екатерины,

семьи Михаила и Петра дружат друг с другом.

Тогда множество X и множество перечисленных отношений Y могут служить теоретико-множественной моделью двух дружественных семей.

Модель называется логической, если она представима предикатами, логическими функциями.

Например, совокупность логических функций вида:

z = x y x, p = x y

есть математическая логическая модель работы дискретного устройства.

Игровые модели

Модель игровая, если она описывает, реализует некоторую игровую ситуацию между участниками игры.

Пример. Пусть игрок 1 - добросовестный налоговый инспектор, а игрок 2 - недобросовестный налогоплательщик. Идет процесс (игра) по уклонению от налогов (с одной стороны) и по выявлению сокрытия уплаты налогов (с другой стороны). Игроки выбирают натуральные числа i и j (i, j n), которые можно отождествить, соответственно, со штрафом игрока 2 за неуплату налогов при обнаружении игроком 1 факта неуплаты и с временной выгодой игрока 2 от сокрытия налогов. Если в качестве модели взять матричную игру с матрицей выигрышей порядка n, то в ней каждый элемент определяется по правилу aij = |i - j|. Модель игры описывается этой матрицей и стратегией уклонения и поимки. Эта игра - антагонистическая.

Лингвистические модели

Модель называется языковой, лингвистической, если она представлена некоторым лингвистическим объектом, формализованной языковой системой или структурой.

Иногда такие модели называют вербальными, синтаксическими.

Например, правила дорожного движения - языковая, структурная модель движения транспорта и пешеходов на дорогах.

Пусть B - множество производящих основ существительных, C - множество суффиксов, P - прилагательных, b_i – корень слова; "+" - операция конкатенации слов, ":=" - операция присваивания, "=>" - операция вывода (выводимости новых слов), Z - множество значений (смысловых) прилагательных.

Языковая модель M словообразования может быть представлена:

<p_i> = <b_i> + <с_i>.

При b_i - "рыб(а)", с_i - "н(ый)", получаем по этой модели p_i - "рыбный", z_i - "приготовленный из рыбы".

Система клеточных автоматов

Модель клеточно-автоматная, если она представима клеточным автоматом или системой клеточных автоматов.

Клеточный автомат - дискретная динамическая система, аналог физического (непрерывного) поля. Клеточно-автоматная геометрия - аналог евклидовой геометрии. Неделимый элемент евклидовой геометрии - точка, на основе ее строятся отрезки, прямые, плоскости и т.д.

Неделимый элемент клеточно-автоматного поля - клетка, на основе её строятся кластеры клеток и различные конфигурации клеточных структур. Представляется клеточный автомат равномерной сетью клеток ("ячеек") этого поля. Эволюция клеточного автомата разворачивается в дискретном пространстве - клеточном поле.

Смена состояний в клеточно-автоматном поле происходит одновременно и параллельно, а время идет дискретно. Несмотря на кажущуюся простоту их построения, клеточные автоматы могут демонстрировать разнообразное и сложное поведение объектов, систем.

В последнее время они широко используются при моделировании не только физических, но и социально-экономических процессов.

Фрактальные модели

Модель называется фрактальной, если она описывает эволюцию моделируемой системы эволюцией фрактальных объектов.

Если физический объект однородный (сплошной), т.е. в нем нет полостей, то можно считать, что его плотность не зависит от размера. Например, при увеличении параметра объекта R до 2R масса объекта увеличится в R² раз, если объект- круг и в R³ раз, если объект - шар, т.е. существует связь массы и длины. Пусть n - размерность пространства. Объект, у которого масса и размер связаны называется "компактным". Его плотность можно рассчитать по формуле:

Если объект (система) удовлетворяет соотношению M(R) ~ R^f(n), где f(n) < n, то такой объект называется фрактальным.

Его плотность не будет одинаковой для всех значений R, то она масштабируется согласно формуле:

Так как f(n) - n < 0 по определению, то плотность фрактального объекта уменьшается с увеличением размера R, а ρ(R) является количественной мерой разряженности объекта.

Пример фрактальной модели - множество Кантора. Рассмотрим отрезок [0;1]. Разделим его на 3 части и выбросим средний отрезок. Оставшиеся 2 промежутка опять разделим на три части и выкинем средние промежутки и т.д. Получим множество, называемое множеством Кантора. В пределе получаем несчетное множество изолированных точек (рис. 1.4)

 

 

 

 

Рис. 1.4. Множество Кантора для 3-х делений

 

Генетические алгоритмы

Идея генетических алгоритмов "подсмотрена" у систем живой природы, у которых эволюция развертывается достаточно быстро.

Генетический алгоритм - это алгоритм, основанный на имитации генетических процедур развития популяции в соответствии с принципами эволюционной динамики.

Генетические алгоритмы используются для решения задач оптимизации (многокритериальной), для задач поиска и управления.

Данные алгоритмы адаптивны, они развивают решения и развиваются сами.

. Генетический алгоритм может быть построен на основе следующей укрупненной процедуры:.

Хотя генетические алгоритмы и могут быть использованы для решения задач, которые, нельзя решить другими методами, они не гарантируют нахождение оптимального решения, по крайней мере, за приемлемое время. Здесь более уместны критерии типа "достаточно хорошо и достаточно быстро".

Главное же преимущество их использования заключается в том, что они позволяют решать сложные задачи, для которых не разработаны пока устойчивые и приемлемые методы, особенно на этапе формализации и структурирования системы.

Генетические алгоритмы эффективны в комбинации с другими классическими алгоритмами и эвристическими процедурами.

 

 

Статические и динамические, дискретные и непрерывные модели

Классификацию моделей проводят по различным критериям.

Модель называется статической, если среди параметров, участвующих в ее описании, нет временного параметра. Статическая модель в каждый момент времени дает лишь "фотографию" системы, ее срез.

Пример. Закон Ньютона F=a*m - это статическая модель движущейся с ускорением a материальной точки массой m. Эта модель не учитывает изменение ускорения от одной точки к другой.

Модель динамическая, если среди ее параметров есть временной параметр, т.е. она отображает систему (процессы в системе) во времени.

Пример. Динамическая модель закона Ньютона будет иметь вид:

F(t)=a(t)*m(t).

Модель дискретная, если она описывает поведение системы только в дискретные моменты времени.

Пример. Если рассматривать только t=0, 1, 2, …, 10 (сек), то модель

St=gt2/2

или числовая последовательность: S0=0, S1=g/2, S2=2g, S3=9g/2,:, S10=50g может служить дискретной моделью движения свободно падающего тела.

Модель непрерывная, если она описывает поведение системы для всех моментов времени некоторого промежутка времени.

Пример. Модель S=gt2/2, 0 < t < 100 непрерывна на промежутке времени (0;100).

Модель имитационная, если она предназначена для испытания или изучения возможных путей развития и поведения объекта путем варьирования некоторых или всех параметров модели.

Пример. Пусть модель экономической системы производства товаров двух видов 1 и 2, в количестве x1 и x2 единиц и стоимостью каждой единицы товара a1 и a2 на предприятии описана в виде соотношения:

a1x1 + a2x2 = S,

где S - общая стоимость произведенной предприятием всей продукции (вида 1 и 2). Можно ее использовать в качестве имитационной модели, по которой можно определять (варьировать) общую стоимость S в зависимости от тех или иных значений объемов и стоимости производимых товаров.