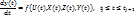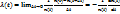Идентификация, модели и их характеристики

Идентификация, модели и их характеристики

Под идентификацией понимается определение структуры и параметров модели, обеспечивающих наилучшее совпадение выходных сигналов модели и объекта, при одинаковых входных воздействиях.

Модель – это представление объекта или системы в некоторой форме отличной от формы их реального существования. Модели могут принимать самую различную форму и записываться с разной степенью математической детализации. Для описания свойств некоторых объектов используют числовые таблицы или графики. Мат. модель представляет собой формализованное мат. описание, отражающее с требуемой точностью процессы, происходящие в исследуемом объекте.

Модели можно классифицировать на:

· Физические и математические

· Статические и динамические

· Детерминированные и стохастические

· Дискретные и непрерывные

· Линейные и нелинейные

· Сосредоточенные и распределенные

· Стационарные и нестационарные

 

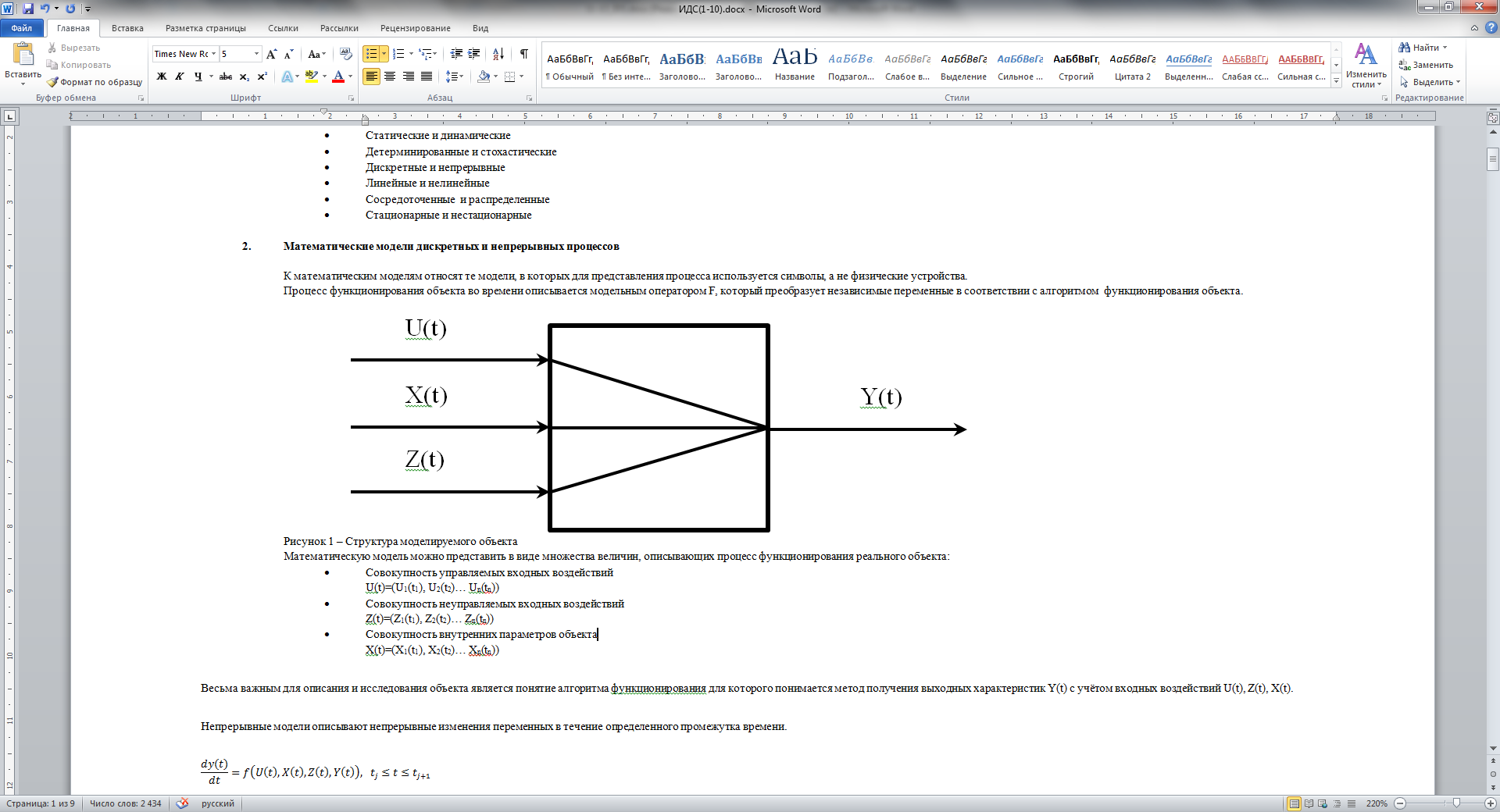
Математические модели дискретных и непрерывных процессов

К математическим моделям относят те модели, в которых для представления процесса используется символы, а не физические устройства.

Процесс функционирования объекта во времени описывается модельным оператором F, который преобразует независимые переменные в соответствии с алгоритмом функционирования объекта.

 

Рисунок 1 – Структура моделируемого объекта

Математическую модель можно представить в виде множества величин, описывающих процесс функционирования реального объекта:

· Совокупность управляемых входных воздействий

U(t)=(U1(t1), U2(t2)… Un(tn))

· Совокупность неуправляемых входных воздействий

Z(t)=(Z1(t1), Z2(t2)… Zn(tn))

· Совокупность внутренних параметров объекта

X(t)=(X1(t1), X2(t2)… Xn(tn))

Весьма важным для описания и исследования объекта является понятие алгоритма функционирования для которого понимается метод получения выходных характеристик Y(t) с учётом входных воздействий U(t), Z(t), X(t).

Непрерывные модели описывают непрерывные изменения переменных в течение определенного промежутка времени.

Дискретная модель описывает зависимость между переменными объекта в дискретные моменты времени.

 

Адекватность модели, критерии адекватности

Всё то, на что направлено человеческая деятельность называется объектом. Замещение одного объекта другим с целью получения информации о важнейших свойствах оригинала с помощью объекта называется регулированием. В модели должны быть учтены все наиболее существенные факторы, влияющие на процесс, вместе с тем она не должна быть загромождена множеством второстепенных факторов, учёт которых усложнит математический анализ. В зависимости от степени полноты математического описания можно выделить два предельных случая:

· Известна полная система уравнений, описывающая все стороны моделирующего процесса и числовые значения параметров уравнений

· Полное математическое описание отсутствует

Таким образом, можно сделать вывод, что если результаты моделирования подтверждаются и могут служить основой для прогнозирования процессов, то говорят, что модель адекватна объекту.

С целью построения наиболее адекватной модели в настоящее время получил развитие системный подход.

Индивидуальный подход подразумевает переход от частного к общему и синтезирует систему путем слияния её компонентов.

Системный подход предполагает переход от общего к частному, когда в основе рассмотрения лежит цель, причем исследуемый объект выделяется из окружающей среды. Важным для системного подхода является определение структуры системы – это восстановление совокупностей связей между элементами системы, отражающими их взаимодействие при структурном подходе выявляются состав системы и связи между ними.

 

Агрегирование систем

Агрегирование – это объединение нескольких элементов в единое целое. Необходимость агрегирования может вызываться обычными целями и сопровождаться разными обстоятельствами, что приводит к различным способам агрегирования. Результатом агрегирования называют агрегатом. Будучи объединенными, взаимодействующие элементы образуют систему, которая обладает не только внешней целостностью, но и природным единством. Наиболее яркое проявление целостности систем состоит в том, что свойства в системе являются суммой не только свойств её составных частей, но и появление новых свойств.

Виды агрегирования:

· Конфигуратор

Всякое описание системы в различных терминах качественно различающихся языков позволяет более полно описать систему

· Агрегаты-операторы

Простейший способ агрегирования состоит в установлении эквивалентности между агрегирующими элементами

· Агрегаты-структуры

Важной формой агрегирования является образование структур. Структуры являются моделью системы и следовательно определяется тройственной совокупностью: объекта, цели и средства моделирования.

Рассмотрим пример агрегирования.

Создание счётчика на основе JK-триггера.

Рисунок 1 - Условное графическое обозначение JK-триггера

На базе JK-триггера возможно построить D-триггер или Т-триггер. Как можно видеть в таблице 1, он переходит в инверсное состояние каждый раз при одновременной подаче на входы J и K логической 1. Это свойство позволяет создать на базе JK-триггера Т-триггер, объединив входы J и К.

 

Таблица 1 – Таблица истинности JK-триггера

J	K	Q(t)	Q(t+1)

Алгоритм функционирования JK-триггера можно представить формулой

 

Соединим три JK-триггера и получим трёхразрядный двоичный счётчик.

Рисунок 2 – Логическая схема трёхразрядного двоичного счётчика

Рисунок 2 – Логическая схема трёхразрядного двоичного счётчика

Рисунок 3 – Условное графическое изображение трёхразрядного двоичного счётчика

Принцип работы счётчика можем рассмотреть по таблице 2

Таблица 2 – Принцип действия двоичного счётчика

Фаза	D0	D1	D2

 

Таким образом, свойства агрегата не сводятся к совокупности свойств его частей, система в целом обладает принципиально новым качеством. Это качество существует, пока существует связь между элементами системы.

 

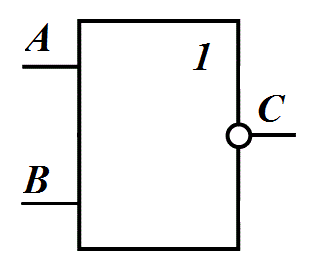
Декомпозиция систем

Декомпозиция – это операция противоположная агрегированию, т.е. выполнение операций разделений целого на части. Она позволяет составить правильное определение общего эффекта системы.

Рассмотрим пример декомпозиции.

Разберем принцип действия логического элемента ИЛИ-НЕ(отрицающее ИЛИ).

 

Рисунок 4 – Условное графическое изображение элемента ИЛИ-НЕ

 

Таблица 3 – Таблица истинности элемента ИЛИ-НЕ

A	B	C

 

Используя таблицу истинности, мы можем разложить логический элемент ИЛИ-НЕ на составные части.

Рисунок 5 – Структурная схема логического элемента ИЛИ-НЕ

Мы видим, что отрицающее ИЛИ состоит из двух элемент ИЛИ и НЕ

Таблица 4 – Таблица истинности логического элемента ИЛИ

A	B	C

 

Таблица 5 – Таблица истинности логического элемента НЕ

A	C

Таким образом, основанием для декомпозиции является содержательная модель системы. Это означает, что в разделяемом целом мы должны найти часть соответствующую каждому элементу модели данной системы. Один из способов упрощения сложного – метод декомпозиции, состоит в разложении сложного на более мелкие составные части.

Принцип частотной модуляции

Модуляция – процесс изменения параметров физического носителя по определенному закону. В качестве физического носителя используется высокочастотные колебания (гармонич.) Закон изменения определяется передаваемым сообщением. Результирующее колебание с изменяющимися во времени параметрами называется модулированным сигналом.

 

При частотной модуляции несущий сигнал является более высокочастотным по отношению к информационному сигналу и амплитуда частотно-модулированного сигнала является неизменной. Частотно модулированный сигнал отличается высокой помехозащищенностью и используется для высококачественной передачи информации: в радиовещании, телевидении, радиотелефонии и др. Основными характеристиками частотной модуляции являются девиация (отклонение) и индекс модуляции. Девиация частоты (frequency deviation) – наибольшее отклонение значения модулированного сигнала от значения его несущей частоты. Единицей девиации частоты является герц (Hz), а также кратные ему единицы. Индекс модуляции (modulation index) – отношение девиации частоты к частоте модулирующего сигнала.

 

Частотная модуляция (ЧМ) — вид аналоговой модуляции, при котором информационный сигнал управляет частотой несущего колебания. По сравнению с амплитудной модуляцией здесь амплитуда остаётся постоянной.

Принцип фазовой модуляции

Модуляция – процесс изменения параметров физического носителя по определенному закону. В качестве физического носителя используется высокочастотные колебания (гармонич.) Закон изменения определяется передаваемым сообщением. Результирующее колебание с изменяющимися во времени параметрами называется модулированным сигналом.

 

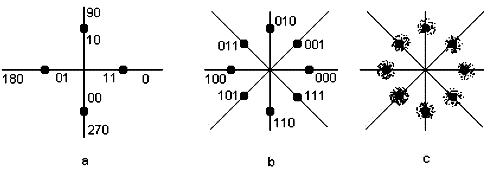
Фазовая и фазоразностная модуляция (ФМ). Суть ФМ заключается в том, что один из двух синусоидальных сигналов имеет некоторый сдвиг по фазе, и этот сдвиг при помощи другого сигнала можно замерить и использовать для передачи данных. Например, в одном периоде сигнала можно закодировать несколько бит информации: сдвигу на 0 градусов можно присвоить двухбитное значение 11, сдвигу на 90 градусов — 10, на 180 градусов — 01, на 270 градусов — 00

Рисунок – Сдвиг по фазе двух сигналов на 90 градусов

Нужно обратить внимание на то, что сдвиг по фазе очередного сигнала замеряется относительно предыдущей фазы. Другими словами, припередачи данных важно не то, какая у сигнала фаза, а какой переход был с одной фазы в другую. Поэтому фазовую модуляцию еще очень часто называют фазоразностной модуляцией.

Для более наглядного представления ФМ изобразим фазовую диаграмму в полярной системе координат. Точки фазовой диаграммы имеют две координаты: угол поворота (µ, соответствует фазовому сдвигу сигнала) и радиус-вектор (r, соответствует амплитуде сигнала). На рис. 3(а) изображена фазовая диаграмма с четырьмя фазовыми сдвигами в 90 градусов. Если модем способен различать восемь разных фазовых сдвига, то в одной амплитуде сигнала можно закодировать три бита (рис. 3, b). Конечно же, каждому здравомыслящему человеку захотелось бы увеличить число фазовых сдвигов, тем самым повысив число передаваемых битов. Но везде есть свой предел, и в этом случае нас ограничивает зашумленность линии: ведь в реальности сигнал не попадает прямо в точки состояния, а ложится вокруг них в виде некого облака (рис. 3, с). Таким образом, чем больше точек состояния, тем труднее модему разобраться, какое положение сигнала принадлежит той или иной точке состояния, и тем больше вероятность ошибки. Казалось бы это придел, но благодаря использованию математических вычислений в одном периоде сигнала можно передать не три-четыре, а десять, шестнадцать и даже больше бит данных!

Рисунок – Фазовая модуляция

Алгоритм и его свойства.

Алгоритм – это точная конечная система правил, определяющая содержание и принцип действия исполнителя над некоторыми объектами. Каждое действие представления алгоритмов должно быть закончено, прежде чем он приступит к исполнению следующего действия:

· Произвести каждое отдельное действие исполнителю предписывает специальное указание, называемое командой. Запись алгоритма должна быть такой, чтобы на каждом шаге его выполнения было известно какую команду надо выполнить в следующем. Это свойство называется точностью.

· Алгоритм может быть выполнен только исполнителем, который понимает каждую команду алгоритма и может исполнить её. Это свойство называется понятностью.

· Алгоритм не должен оставлять места произвола. Это свойство называется определённостью.

· Результативность; смысл этого свойства состоит в том, что при точном исполнении команд алгоритма процесс должен прекратиться за конечное число шагов, и при этом должен быть получен ответ на вопрос задачи.

· Массовость, т.е. способность решения любой задачи из некоторого класса задач.

Основные понятия теории надёжности

Неисправность – состояние объекта, при котором он не соответствует хотя бы одному своему параметру, указанному в эксплутационной документации

Неработоспособность -Состояние обьекта, при котором он не способен выполнять все свои функции

Дефект – Каждое несоответствие обьекта установленным требованиям

Отказом называется состояние заключающееся в нарушении работоспособности обьекта. Факт отказа устанавливается на основании некоторых примеров отказа, т. е признаков, позволяющих судить о нарушении работоспособности.

Наработкой называется продолжительность работы обьекта выраженная в единицах времени ли бо в количестве циклов. Разделим нароботку. Различают наработку до отказа (от начала работы до 1 отказа) и наработку между отказами (от ремонта до очередного отказа)

Среднюю наработку между отказами называют Наработкой на отказ

Коэффициент готовности – вероятность того, что обьект окажется работоспособным в произвольный момент времени, кроме запланированных периодов в течении которых его работа по назначению не предусмотрена

Надёжность – свойство обьекта сохранять во времени всех параметров и выполнять требуемые функции в заданных условиях применения.

Интенсивностью отказов называется условная плотность вероятности возникновения отказа обьекта при условии что до рассматриваемого момента времени отказы не возник

При испытаниях на надёжность количество исправных элементов n(t) с течением времени t уменьшается за счёт того, что часть из них n(t) – n(t+∆t) становится неисправным в результате отказа

Интенсивность отказа определяется пределом:

21 Классификация датчиков и основные требования предъявляемые к ним.

Датчики (измерительные преобразователи, сенсоры) являются элементами, с помощью которых получают информацию о параметрах контролируемой системы или устройств.

Датчик – элемент измерительного сигнального регулирующего или управляющего устройства, преобразующий контролируемую величину (температуру, давление, частоту…) в сигнал удобный для измерения передачи хранения, обработки, регистрации а иногда и для воздействия на управляющие процессы. Таким образом датчик это устройство преобразующее входное воздействие любой физической величины в сигнал, удобный для дальнейшего использования.

Используемые датчики могут быть классифицированы по различным признакам:

В зависимости от вида входной величины различают: Датчики скорости, ускорения, усилия, температуры, положения, электрические датчики…

По видам выходной величины различают неэлектрические и электрические датчики: Датчики постоянного тока, датчики амплитуды переменного тока, датчики частоты переменного тока, датчики сопротивления.

Большенство датчиков являются электрическими. Это обусловлено: 1-Электрические величины удобно передовать на расстояния с большой скоростю, 2 универсальность эл. Величин, которая заключается в том, что каждую из них можно выразить через другие. 3 Эл. Вел. Просто преобразуются в цифровой код

По принципу действия - Генераторные, параметрические. Генераторные датчики входную вел. Преобразуют в изменение какого либо параметра (R, L, C)

По принципу действия датчики так же можно разделить на: Оммические, реостатные, фотоэлектрические, индуктивные, ёмкостные и др.

Различают 3 класса датчиков: Аналоговые (датчики вырабатывающие аналоговый сигнал), Цифровые, Бинарные (вырабатывающие сигнал только 2х уровний 0 или 1)

Требования предъявляемые к датчикам: Однозначная зависимость выходной величины от входной, стабильность, Высокая чувствительность, малые размеры, отсутствие обратного воздействия на контролируемый процесс

 

Идентификация, модели и их характеристики

Под идентификацией понимается определение структуры и параметров модели, обеспечивающих наилучшее совпадение выходных сигналов модели и объекта, при одинаковых входных воздействиях.

Модель – это представление объекта или системы в некоторой форме отличной от формы их реального существования. Модели могут принимать самую различную форму и записываться с разной степенью математической детализации. Для описания свойств некоторых объектов используют числовые таблицы или графики. Мат. модель представляет собой формализованное мат. описание, отражающее с требуемой точностью процессы, происходящие в исследуемом объекте.

Модели можно классифицировать на:

· Физические и математические

· Статические и динамические

· Детерминированные и стохастические

· Дискретные и непрерывные

· Линейные и нелинейные

· Сосредоточенные и распределенные

· Стационарные и нестационарные