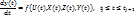Математические модели дискретных и непрерывных процессов

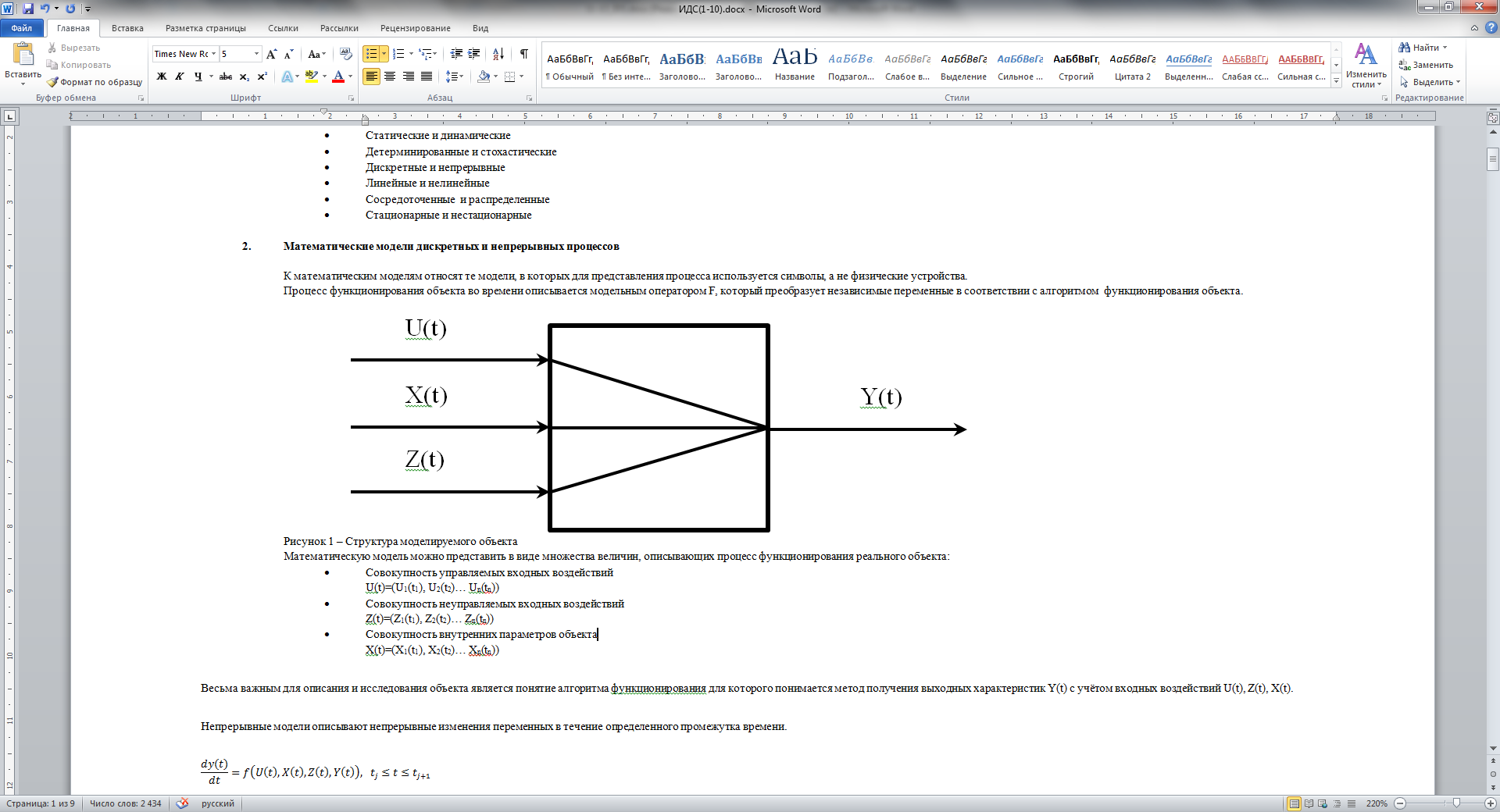
К математическим моделям относят те модели, в которых для представления процесса используется символы, а не физические устройства.

Процесс функционирования объекта во времени описывается модельным оператором F, который преобразует независимые переменные в соответствии с алгоритмом функционирования объекта.

 

Рисунок 1 – Структура моделируемого объекта

Математическую модель можно представить в виде множества величин, описывающих процесс функционирования реального объекта:

· Совокупность управляемых входных воздействий

U(t)=(U1(t1), U2(t2)… Un(tn))

· Совокупность неуправляемых входных воздействий

Z(t)=(Z1(t1), Z2(t2)… Zn(tn))

· Совокупность внутренних параметров объекта

X(t)=(X1(t1), X2(t2)… Xn(tn))

Весьма важным для описания и исследования объекта является понятие алгоритма функционирования для которого понимается метод получения выходных характеристик Y(t) с учётом входных воздействий U(t), Z(t), X(t).

Непрерывные модели описывают непрерывные изменения переменных в течение определенного промежутка времени.

Дискретная модель описывает зависимость между переменными объекта в дискретные моменты времени.

 

Адекватность модели, критерии адекватности

Всё то, на что направлено человеческая деятельность называется объектом. Замещение одного объекта другим с целью получения информации о важнейших свойствах оригинала с помощью объекта называется регулированием. В модели должны быть учтены все наиболее существенные факторы, влияющие на процесс, вместе с тем она не должна быть загромождена множеством второстепенных факторов, учёт которых усложнит математический анализ. В зависимости от степени полноты математического описания можно выделить два предельных случая:

· Известна полная система уравнений, описывающая все стороны моделирующего процесса и числовые значения параметров уравнений

· Полное математическое описание отсутствует

Таким образом, можно сделать вывод, что если результаты моделирования подтверждаются и могут служить основой для прогнозирования процессов, то говорят, что модель адекватна объекту.

С целью построения наиболее адекватной модели в настоящее время получил развитие системный подход.

Индивидуальный подход подразумевает переход от частного к общему и синтезирует систему путем слияния её компонентов.

Системный подход предполагает переход от общего к частному, когда в основе рассмотрения лежит цель, причем исследуемый объект выделяется из окружающей среды. Важным для системного подхода является определение структуры системы – это восстановление совокупностей связей между элементами системы, отражающими их взаимодействие при структурном подходе выявляются состав системы и связи между ними.

 

Агрегирование систем

Агрегирование – это объединение нескольких элементов в единое целое. Необходимость агрегирования может вызываться обычными целями и сопровождаться разными обстоятельствами, что приводит к различным способам агрегирования. Результатом агрегирования называют агрегатом. Будучи объединенными, взаимодействующие элементы образуют систему, которая обладает не только внешней целостностью, но и природным единством. Наиболее яркое проявление целостности систем состоит в том, что свойства в системе являются суммой не только свойств её составных частей, но и появление новых свойств.

Виды агрегирования:

· Конфигуратор

Всякое описание системы в различных терминах качественно различающихся языков позволяет более полно описать систему

· Агрегаты-операторы

Простейший способ агрегирования состоит в установлении эквивалентности между агрегирующими элементами

· Агрегаты-структуры

Важной формой агрегирования является образование структур. Структуры являются моделью системы и следовательно определяется тройственной совокупностью: объекта, цели и средства моделирования.

Рассмотрим пример агрегирования.

Создание счётчика на основе JK-триггера.

Рисунок 1 - Условное графическое обозначение JK-триггера

На базе JK-триггера возможно построить D-триггер или Т-триггер. Как можно видеть в таблице 1, он переходит в инверсное состояние каждый раз при одновременной подаче на входы J и K логической 1. Это свойство позволяет создать на базе JK-триггера Т-триггер, объединив входы J и К.

 

Таблица 1 – Таблица истинности JK-триггера

J	K	Q(t)	Q(t+1)

Алгоритм функционирования JK-триггера можно представить формулой

 

Соединим три JK-триггера и получим трёхразрядный двоичный счётчик.

Рисунок 2 – Логическая схема трёхразрядного двоичного счётчика

Рисунок 2 – Логическая схема трёхразрядного двоичного счётчика

Рисунок 3 – Условное графическое изображение трёхразрядного двоичного счётчика

Принцип работы счётчика можем рассмотреть по таблице 2

Таблица 2 – Принцип действия двоичного счётчика

Фаза	D0	D1	D2

 

Таким образом, свойства агрегата не сводятся к совокупности свойств его частей, система в целом обладает принципиально новым качеством. Это качество существует, пока существует связь между элементами системы.

 

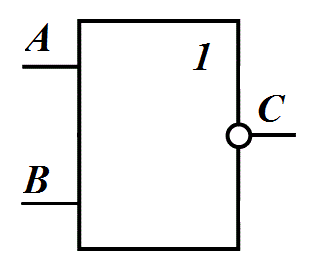
Декомпозиция систем

Декомпозиция – это операция противоположная агрегированию, т.е. выполнение операций разделений целого на части. Она позволяет составить правильное определение общего эффекта системы.

Рассмотрим пример декомпозиции.

Разберем принцип действия логического элемента ИЛИ-НЕ(отрицающее ИЛИ).

 

Рисунок 4 – Условное графическое изображение элемента ИЛИ-НЕ

 

Таблица 3 – Таблица истинности элемента ИЛИ-НЕ

A	B	C

 

Используя таблицу истинности, мы можем разложить логический элемент ИЛИ-НЕ на составные части.

Рисунок 5 – Структурная схема логического элемента ИЛИ-НЕ

Мы видим, что отрицающее ИЛИ состоит из двух элемент ИЛИ и НЕ

Таблица 4 – Таблица истинности логического элемента ИЛИ

A	B	C

 

Таблица 5 – Таблица истинности логического элемента НЕ

A	C

Таким образом, основанием для декомпозиции является содержательная модель системы. Это означает, что в разделяемом целом мы должны найти часть соответствующую каждому элементу модели данной системы. Один из способов упрощения сложного – метод декомпозиции, состоит в разложении сложного на более мелкие составные части.