
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Богачков И. В., Майстренко В. А.Содержание книги
Поиск на нашем сайте
И. В. Богачков, В. А. Майстренко
Основы теории Радиоавтоматических систем
Учебное пособие Часть 1.
Рекомендовано УМО по образованию в области телекоммуникаций в качестве учебного пособия для студентов высших учебных заведений, обучающихся по специальности 210402 – Средства связи с подвижными объектами – Телекоммуникации
Омск Издательство ОмГТУ УДК 621.51: 621.37/.39 ББК 32.965+32.84 Б73
Рецензенты:
Н. И. Горлов, д-р техн. наук, профессор, зав. каф. «Линии связи» Сибирского государственного университета телекоммуникаций и информатики, г. Новосибирск;
Ю. А. Пальчун, д-р техн. наук, профессор, академик Метрологической академии, ученый секретарь СНИИМ.
Богачков И. В., Майстренко В. А. Б 73 Основы теории радиоавтоматических систем: Учеб. пособие. Часть 1. – Омск: Изд-во ОмГТУ, 2009. – 164 с. ISBN
Учеб. пособие разработано на кафедре «Средства связи и информационная безопасность» и предназначено для студентов, обучающихся по направлениям подготовки дипломированных специалистов (специальности 210402 «Средства связи с подвижными объектами» и 210302 «Радиотехника»), бакалавров и магистров направлений «Телекоммуникации» и «Радиотехника», всех форм обучения. Каждая глава содержит основные сведения, контрольные вопросы, список рекомендуемой литературы.
УДК 621.51: 621.37/.39 ББК 32.965+32.84
Печатается по решению редакционно-издательского совета Омского государственного технического университета
ã Омский государственный
Предисловие В соответствии с Государственным стандартом специальности 210302 «Радиотехника» (направление 210300 «Радиотехника») дисциплина «Радиоавтоматика» относится к циклу общепрофессиональных дисциплин. Для успешного усвоения дисциплины «Радиоавтоматика» необходимо знание таких предшествующих дисциплин, как «Высшая математика», «Физика», «Основы теории цепей», «Радиотехнические цепи и сигналы», «Основы автоматизации проектирования радиоэлектронных устройств», «Схемотехника аналоговых электронных устройств». Полученные знания и навыки по данной дисциплине используются при изучении дисциплин специального цикла: «Устройства генерирования и формирования сигналов», «Устройства приема и обработки сигналов», «Основы радиотехнических систем», «Синтезаторы частоты». Учебное пособие содержит 10 глав, в которых отражены все вопросы дисциплины «Радиоавтоматика». Каждая глава состоит из краткого содержания, основных сведений, списка ссылок на рекомендуемую литературу (для упрощения поиска необходимого материала), контрольных вопросов и заданий для самопроверки, ответы на которые помогут изучающим дисциплину в закреплении знаний по каждой главе. При изучении каждой главы следует придерживаться последовательности вопросов, изложенных в ее начале. Рекомендуется следующая схема изучения материала: определение, физическая сущность, практическая значимость, связь с другими понятиями. В приложениях приведены таблицы некоторых оригиналов и изображений преобразования Лапласа и Z -преобразования, некоторые полезные формулы для вычисления коэффициентов ошибок и дисперсии, а также основные схемы, передаточные функции и характеристики простейших динамических звеньев. После изучения материала теоретической части [1 – 5] студент приступает к выполнению контрольных заданий [6] в соответствии со своим вариантом. Список сокращений АПЧ – автоматическая подстройка частоты; АРУ – автоматическая регулировка усиления; АСД – автоматическое слежение по дальности; АСН – автоматическое слежение по направлению; АФЧХ – амплитудно-фазо-частотная характеристика; АЧХ – амплитудно-частотная характеристика; ГУН – генератор, управляемый напряжением; ИХ – импульсная характеристика (g (t)); ЛАЧХ – логарифмическая амплитудно-частотная характеристика (L (w)); ЛФЧХ – логарифмическая фазо-частотная характеристика (j(w)); ОГ – эталонный генератор; ОУ – объект управления; ПГ – подстраиваемый генератор; ПИФ – пропорционально-интегрирующий фильтр; ПФ – передаточная функция; ПХ – переходная характеристика (h (t)); ПЧ – промежуточная частота; РА – радиоавтоматика; РАС – радиоавтоматическая система; РПрмУ – радиоприемное устройство; САР – система автоматического регулирования; САУ – система автоматического управления; СКО – среднеквадратическая ошибка (отклонение); СЧ – синтезатор частоты; УЭ – управляющий элемент; ФАПЧ – фазовая автоподстройка частоты; ФД – фазовый детектор; ФНЧ – фильтр нижних частот; ФЧХ – фазо-частотная характеристика (j(w)); ЧАП – частотная автоподстройка; ЧД – частотный дискриминатор; ЧПФ – частотная передаточная функция; ЭГ – эталонный генератор; х (t) – функция, описывающая сигнал ошибки РАС; y (t) – функция, описывающая выходной процесс РАС; γ – перерегулирование; l(t) – функция, описывающая внешнее воздействие; x(t) – функция, описывающая внешнее возмущение; z – коэффициент демпфирования (относительный коэффициент затухания) колебательной системы. Введение Радиоавтоматика (РА) – учебная дисциплина, изучающая принципы построения, методы анализа и синтеза автоматических систем современных радиотехнических устройств, используемых для целей радиосвязи, радиолокации, радионавигации, радиовещания и в других областях. Автоматизация – одно из важнейших направлений научно-технического прогресса. Качество радиоавтоматических систем (РАС) во многом определяет возможности и характеристики радиоаппаратуры. Без прочного усвоения принципов радиоавтоматического управления невозможно проектирование радиоэлектронной аппаратуры, отвечающей современным требованиям. Теоретическую основу дисциплины «Радиоавтоматика» составляет кибернетика – наука об общих законах получения, хранения, передачи и преобразования информации в сложных управляющих системах. Специфическая особенность РАС заключается в том, что в них обработка сигналов осуществляется радиотехническими методами. Целью преподавания дисциплины «РА» является изучение основных принципов построения и области применения РАС, основных разновидностей РАС, математических методов описания и исследования непрерывных, дискретных, цифровых РАС и их звеньев, методов анализа устойчивости и параметров качества РАС, методов синтеза и оптимизации РАС. В результате изучения дисциплины студенты должны знать структуры и принципы действия основных РАС, физические процессы, протекающие в РАС при эксплуатации, основные виды детерминированных и случайных сигналов, используемых в РАС, специфику описания динамических звеньев РАС различных типов и их основные характеристики, научиться проводить анализ и инженерный синтеза РАС. Типовые схемы САР
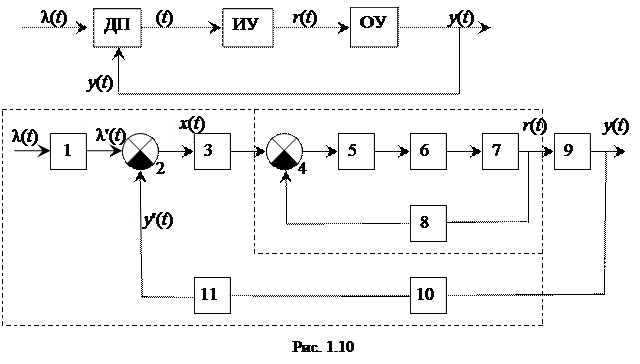
На рис. 1.10 показана САР: 1 – датчик программы; 2 и 4 – элементы сравнения (см. рис. 1.11); 3 – преобразующее устройство; 5 и 8 – корректирующие устройства, соответственно последовательного и параллельного вида (для придания определенных динамических свойств); 6 – усилитель; 7 – исполнительное устройство; 9 – ОУ; 10 – измерительное устройство; 11 – элемент главной обратной связи. САР делят на системы прямого и непрямого регулирования; на одноконтурные и многоконтурные. Если кроме главной ОС имеется ещё и местная (пример местной обратной связи – связь с выхода элемента 7 через корректирующее устройство 8 на элемент сравнения 4.), то говорят о многоконтурной САР.
Взаимные системы – системы, в которых существуют взаимные преднамеренные связи между петлями регулирования отдельных величин. РАС классифицируются § по виду уравнений динамики в процессах управления; § по характеру формирования сигналов управления; § по характеру процессов управления; § по характеру функционирования. На основе этой классификации выбирается математический признак. По виду уравнений динамики РАС разделяются на линейные и нелинейные, обыкновенные и особые, стационарные и нестационарные. В линейных системах все элементы обладают линейными характеристиками. В определённых пределах многие РАС можно считать линейными. Нелинейные РАС имеют хотя бы один элемент с нелинейной статической характеристикой. Обыкновенные системы – стационарные с сосредоточенными параметрами и описываются линейными динамическими уравнениями. Особые РАС – стационарные системы, которые содержат элементы с распределенными параметрами. Нестационарные РАС описываются динамическими уравнениями с переменными коэффициентами и уравнениями в частных производных. По принципу формирования сигналов САУ делятся на непрерывные и прерывистые. Прерывистые САУ делятся на импульсные, релейные и цифровые. Процессы управления САУ бывают детерминированными и стохастическими (случайными). По характеру функционирования различают обычные, адаптивные и терминальные САУ. Обычные САУ могут выполнять такие задачи: стабилизация, программное регулирование и следящее регулирование. Адаптивные САУ в процессе работы могут менять свой алгоритм. Такие САУ могут самообучаться и самоорганизовываться для достижения оптимальных характеристик. Терминальные САУ могут изменять свой режим работы в определенные моменты времени.
Список рекомендуемой литературы: [ 1, с. 7-10, 26-27, 47-58; 2, с. 4-9; 3, с. 7-18, 32-39, 56-58, 69-90, 102-104, 113-118, 273-282; 4, с. 8-10, 22-24; 5, с. 3-13, 39-45, 49-58, 85-88, 153; 7, с. 3-12; 10, т. 1, с. 5-22, 31-35, 40-44, 64-74, 105-113; 11, с. 5-7, 11-13, 18-21, 49-52, 301-330; 13, с. 7, 11-13, 17-21; 18, с. 7-10, 17-21; 27, с. 12-17]. Контрольные вопросы 1. Что изучает дисциплина «РА»? 2. Что представляет собой объект управления «РА»? 3. Чем автоматическое управление отличается от автоматизированного? 4. Дайте определение системам автоматического регулирования. 5. Какие особенности имеют РАС по сравнению с другими САУ? 6. Какие задачи решают РАС? 7. В чем заключается процесс управления? 8. Дайте определение цели управления и цели регулирования. 9. Чем отличается возмущение от входного воздействия? 10. Дайте определение алгоритмам управления и функционирования. 11. Дайте определение фундаментальным принципам управления. 12. Какие достоинства и недостатки имеет принцип замкнутого управления? 13. Чем отличаются понятия «ошибка» и «отклонение»? 14. Дайте определение статической и астатической системам. 15. Нарисуйте обобщенную функциональную схему САУ. 16. Назовите основные элементы структурной схемы САУ и опишите их назначение. 17. Для чего используются корректирующие устройства? 18. Дайте определение дискриминатора и опишите его назначение в САУ. 19. Как классифицируются САУ по характеру функционирования? 20. Для чего в РАС используется обратная связь? Основных разновидностей рас
Принципы действия основных разновидностей РАС. Обобщенные функциональная и структурная схемы (математические модели) следящих РАС. Основные элементы обобщенной РАС. Уравнения замкнутой следящей системы относительно выходного процесса и ошибки слежения. ПФ замкнутой РАС по ошибке и по возмущению. Основные элементы РАС и их математическое описание. Дискриминаторы и их статические эквиваленты. Дискриминационная и флуктуационная характеристики дискриминаторов. Математическая модель дискриминатора и условия его линейного и стационарного описания. Объекты управления РАС. Функциональные схемы и математическое описание РАС, сведение их к обобщенной следящей системе. Системы частотной автоподстройки частоты (ЧАП). Системы фазовой автоподстройки частоты (ФАПЧ). Слежение за частотой и фазой сигнала. Системы стабилизации частоты и фазы сигнала. Системы автоматической регулировки (стабилизации) усиления (АРУ). Системы слежения за временным положением импульсов. РАС углового сопровождения цели. Системы сопровождения по дальности. РАС настройки и подстройки контуров. Пример 4.1. 1. 4 р 5 + 16 р 4 + 8 р 2 + р + 12 = 0 – система неустойчива, так как коэффициент при р 3 равен нулю. 2. 14 р 3 – 7 р 2 + 2 р + 4 = 0 – система неустойчива, так как коэффициент при р 2 отрицательный. 3. р 5 + 7 р 4 + 8 р 3 + 9 р 2 + 4 р + 2 = 0 – необходимое условие устойчивости выполняется, для определения устойчивости РАС необходимо найти корни полинома. (С помощью «Mathcad» можно проверить, что в данном случае все корни лежат в левой комплексной полуплоскости, а значит, система будет устойчивой.)
Для сложных РАС порядок уравнений может быть значительным, и вычисление корней характеристического полинома оказывается затруднительным. Устойчивость можно оценить, не прибегая к вычислениям корней, с использованием алгебраических и графоаналитических критериев, которые были разработаны во времена, когда не было компьютеров. Хотя в настоящее время вычисление корней характеристического полинома даже больших порядков трудностей не представляет, эти критерии не потеряли актуальности. К алгебраическим относятся критерий А. Гурвица, к частотным – критерии А. В. Михайлова, Г. Найквиста и др. Критерий Гурвица В 1877 г. Э. Раусом был предложен алгебраический критерий устойчивости, который в 1895 г. был представлен в более удобной форме А. Гурвицем. Поэтому данный критерий называют также критерием Рауса – Гурвица [10]. Для уравнения (4.3) anpn + an-1pn-1 +...+ a0 =0 составляется матрица Гурвица:
Порядок составления матрицы Гурвица (4.7) такой. По главной диагонали с верхнего левого угла до правого нижнего записываются с убыванием индексов коэффициенты с an-1 по a0. Над элементами главной диагонали записываются коэффициенты с убывающими индексами, а под элементами главной диагонали – с возрастающими. Для оценки устойчивости необходимо вычислить определители Гурвица, которые получаются из (4.7) путем вычеркивания равного числа строк и столбцов в левом верхнем углу матрицы:
Система будет устойчива, если все определители Гурвица при an > 0 – положительные. Если определитель ∆ n = 0, то система находится на границе устойчивости. Возможны два случая: an = 0 или ∆n–1 = 0. Если an = 0, это соответствует нейтрально-устойчивой системе. Если определитель ∆ n-1 = 0, это соответствует колебательной границе устойчивости. Из условия ∆ n-1 = 0 можно определить параметры, при которых РАС находится на границе устойчивости. Это позволяет вычислить критические параметры (например, постоянные времени звеньев, коэффициент усиления по постоянному току kкр), соответствующие границе устойчивости. Отклонение критической величины от номинальной называется запасом устойчивости.
Пример. 4.2. Рассмотрим линеаризованную систему ФАПЧ при отсутствии внешнего возмущения (Sд – крутизна характеристики дискриминатора, Т2 – постоянная времени форсирующего звена). K λ y (p) =
где K λ y (p) = Характеристическое уравнение, которое также можно было получить с помощью формулы (4.1), имеет вид:
Определяем коэффициенты характеристического полинома an: а3 = ТдТф, а2 = Тд + Тф, а1 = 1 + k0Т2, а0 = Составляем матрицу Гурвица:
Находим определители Гурвица:
В данном примере а1, а2, а3 > 0, но а0 зависит от Sд (kи > 0, kф > 0), которая на разных участках дискриминационной характеристики различна (рис. 4.4). Вне рабочего (линейного) участка Sд < 0, и система неустойчива. На рабочем участке Sд > 0, и необходимое условие устойчивости выполняется.
что в итоге позволяет найти критический коэффициент усиления kкр:
Система будет устойчива, если k0 < kкр . Если форсирующее звено в фильтре отсутствует (Т2 = 0), то Если Т2 увеличивается, то kкр также повышается, а значит устойчивость системы увеличивается. Таким образом, в данной РАС, введение форсирующего звена повышает устойчивость системы. Приравняв нулю знаменатель (4.14), получим, что Для анализа устойчивости САУ с характеристическим полиномом выше пятой степени применяют модификацию критерия Гурвица – критерий П. Льенара – Р. Шипара [10], который можно сформулировать так. Если все коэффициенты характеристического полинома положительны (a j > 0), то достаточное условие устойчивости сводится к тому, чтобы положительными были все определители Гурвица либо четного (D2, D4,.., D2k), либо нечетного индекса (D1, D3,.., D2k-1). (Доказано, что из положительности D2 k следует положительность D2 k -1 [10].) В результате количество определителей Гурвица, которые необходимо вычислить, существенно уменьшается. Критерий Найквиста На практике более широко применяется критерий Г. Найквиста, разработанный в 1932 г. [10], который позволяет судить об устойчивости замкнутой РАС по частотным характеристикам разомкнутой системы. Пусть разомкнутая РАС устойчива и не содержит идеальных интеграторов. Выражение (4.22) отражает связь ПФ разомкнутой и замкнутой систем.
Поскольку у реальных РАС порядок полинома числителя N (p) не может превышать порядок полинома знаменателя D (p), порядки полиномов D (p) и D (p) + N (p) будут одинаковы. Проанализируем характеристический вектор
Числитель (4.23) является характеристическим вектором замкнутой системы, а знаменатель – разомкнутой системы. Пусть характеристическое уравнение замкнутой системы имеет m правых корней (n – m – число левых корней), а характеристическое уравнение разомкнутой системы – l правых корней (n – l – число левых корней). Изменение аргумента вектора F (i ω) при изменении ω от –∞ до +∞ составит
Для устойчивой замкнутой системы m = 0.
Следовательно при изменении ω от 0 до ∞
Если РАС устойчива в разомкнутом состоянии (l = 0), то Таким образом, если разомкнутая и замкнутая системы устойчивы, то изменение аргумента вектора F (i ω) равно нулю, следовательно, его годограф не охватывает начало координат. Если годограф F (i ω) охватывает начало координат, то система в замкнутом состоянии не устойчива. От годографа F (i ω) удобно перейти к годографу разомкнутой системы W (i ω). Если в разомкнутом положении система устойчива, тогда в замкнутом состоянии она также будет устойчива, если годограф Найквиста начинается на действительной полуоси ЧПФ и при изменении ω от 0 до ∞ не охватывает критическую точку (–1, i 0). Если точка (–1, i 0) охватывается, то система в замкнутом состоянии будет неустойчива. Если кривая проходит через точку (–1, i 0), то система нейтральна (находится на границе устойчивости).
На рис. 4.9 показаны годографы F (i ω) (рис. 4.9а) и W (i ω) (рис. 4.9б) устойчивых (график 1) и неустойчивых (график 2) в замкнутом состоянии систем. Если РАС неустойчива в разомкнутом состоянии (l ¹ 0), то для оценки устойчивости системы в замкнутом состоянии существует правило переходов Я. З. Цыпкина: для того, чтобы система, неустойчивая в разомкнутом состоянии, была устойчива в замкнутом состоянии необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов годографа через отрезок вещественной оси слева от критической точки (]–∞, –1[ для W (i ω)) была равна l /2 (l – число правых корней разомкнутой системы). Для годографа W (i ω) при изменении ω от 0 до ∞ переход вещественной оси ]–∞, –1[ называется положительным, если он происходит сверху вниз, и отрицательным, если он происходит снизу вверх. Если РАС содержит v идеальных интеграторов в контуре управления, то начальное значение ФЧХ равно – v p/2, а АЧХ – бесконечности. Для оценки устойчивости таких систем в замкнутом состоянии их дополняют дугой – v p/2 бесконечного радиуса, которая соединяет уходящую в бесконечность линию годографа с положительной вещественной полуосью (см. рис. 4.10). Критерий Найквиста в этом случае применяется к результирующему графику. Если годографы W (i ω) пересекают вещественную ось только справа от критической точки (–1, i 0), такие РАС называют абсолютно устойчивыми. Если система теряет устойчивость не только при повышении коэффициента усиления, но и при его уменьшении (см. рис. 4.10в), то такая система называется условно устойчивой [1]. На рис. 4.10 приведены годографы W (i ω) для систем, которые содержат 1 идеальный интегратор (дуга R = ¥ будет иметь размер 1хp/2, то есть 90°).
На рис. 4.10а построен годограф для системы ФАПЧ из примера 4.2, разомкнутая ЧПФ для которой
а Т2 = 4,7 мс (k0 << kкр). Так как результирующий график не охватывает точку (–1, i 0), система в замкнутом состоянии будет абсолютно устойчивой, что подтверждает сделанные ранее выводы. На рис. 4.10б представлен годограф той же системы при Т2 = 0, k0 = 2 kкр. В этом случае в замкнутом состоянии система будет неустойчивой, так как результирующий график охватывает критическую точку (–1, i 0). На рис. 4.10в показан более сложный случай, когда годограф W (i ω) пересекает вещественную полуось ]–∞, –1[ дважды: один переход положительный, второй отрицательный, – значит, разность числа переходов равна нулю (l /2 = 0). Следовательно, система в замкнутом состоянии будет условно устойчивой.
Второго порядка
ПФ звена второго порядка можно представить в нескольких формах записи:
Возможно представление ПФ в таком виде:
Наиболее общие формы – первая и вторая в (5.34). Третьей в (5.34) пользуются преимущественно для колебательных звеньев. Форма (5.35) удобна исключительно для апериодических звеньев. Свойства апериодического и колебательного позиционных звена отличаются прежде всего разными значениями величин z. Для апериодических звеньев второго порядка z ³ 1. Дляних характерна монотонная форма ПХ и плавная (без подъемов) АЧХ (ЛАЧХ) (прил. 2), имеющая в области высоких частот крутизну спада –40 дБ/дек. ПХ такого звена определяется по формуле (прил. 1)
а ИХ – как
График ПХ h (t), приведенный на рис. 5.8, дает представление об определении параметров ПФ по экспериментальной характеристике. (См. также рис. 5.9 и 5.10, график 4.) Если в (5.35) – (5.37) Т3 = Т4 (z = 1 или Т 1 = 2 Т2 в (5.34)), то
При Т4 ® 0 данное звено вырождается в апериодическое звено первого порядка.
Если параметр демпфирования z лежит в пределах По мере уменьшения z ярче проявляются резонансные свойства звена (рис. 5.10, графики 1 и 2), и соответственно увеличивается колебательность временных характеристик (число пересечений уровня h (¥) (рис. 5.9, графики 1 и 2) и g (¥).
Число полных периодов колебаний N за время регулирования (N = 1 на ПХ рис. 5.11, N = 2 на ПХ рис. 5.9, график 1) Временные характеристики колебательного звена описываются выражением
=
В (5.39) – (5.40)
График на рис. 5.11 иллюстрирует, как по экспериментальной ПХ реального звена можно найти параметры соответствующего колебательного звена. С погрешностью менее 25% при γ ³ 8 %, кроме формул (5.30) и других, приведенных ранее, можно оценить некоторые параметры ПХ с помощью эмпирических формул [13, 17, 20]: Ту 2 = Тн – Ту; Ту 1 = Т 09 – Тзап; Если параметр демпфирования z лежит в пределах
На рис. 5.12 приведены примеры нормированных АЧХ звеньев второго порядка: апериодического (график 1) и колебательного (график 2). Пример 5.2. Проанализируем показатели качества и взаимосвязь временных и частотных характеристик на примере апериодического и колебательного звеньев. За основу возьмем частотные зависимости (АЧХ), показанные на рис. 5.10. Частота w на этих графиках изменяется от 0 до 22 рад/с. Для графика 1 получаем (z1 = 0,3): М = 1,93, w0 = 9,3 рад/с, wп = 5,9 рад/с, wср = 13,1 рад/с, w07 = 14,7 рад/с, w05 = 16,8 рад/с. Для графика 2 находим (z2 = 0,5): М = 1,15, w0 = 6,9 рад/с, wп = 11,7 рад/с, wср = 10,0 рад/с, w07 = 12,7 рад/с, w05 = 15,3 рад/с. Для графика 3 – (z3 = 0,8): М = 1, wп = w07 = 8,7 рад/с, w05 = 12,7 рад/с. Для графика 4 – (z4 = 1,1): М = 1, wп = w07 = 5,6 рад/с, w05 = 15,3, рад/с. С помощью формулы (5.29) оценим Тр : Тр1 = 0,5…2,0 с, Тр2 = 0,3…1,1 с, Тр3 = 0,36…1,4 с, Тр4 = 0,56…2,2 с. Оценим с помощью формулы (5.30) Тр и γ при М > 1: Тр1 = 1,4 с, γ1= 48%, Тр2 = 0,57 с, γ2= 9%. Зная w0, найдем период Тк и частоту колебаний wк ПХ с помощью (5.40): w1к = 8,9 рад/с, w2к = 5,7 рад/с, Т1к = 0,7 с, Т2к = 1,1 с. Сравним полученные результаты с прямыми оценками показателей качества, которые определяются из графиков ПХ, показанных на рис. 5.9 (t изменяется от 0 до 1,2 с): Тр1 = 1,07 с, Тр2 = 0,53 с, Тр3 = 0,34 с, Тр4 = 0,47 с; γ1 = 42%, γ2 = 15%, γ3 = 2%, γ4 = 0%, Т1к = 0,7 с, Т2к > 1 с. К (w=0) = h (¥) = k 0. К (w®¥) = h (0)=0. Оценим с помощью формулы (5.42) временные параметры (рис. 5.11) ПХ при М > 1: для графика 1 (z= 0,3) получаем Ту1 = 0,02 с, Ту2 = 0,19 с; а для графика 2 (z= 0,5) – Ту1 = 0,09 с, Ту2 = 0,21 с (эти параметры позволяют оценить скорость нарастания ПХ на начальном участке). Сравним полученные результаты с оценками показателей качества, которые можно определить из графиков ПХ, показанных на рис. 5.9. Для графика 1 (z= 0,3) получаем Т 09 – Тзап = Ту1 = 0,05 с, Тн – Ту = = Ту2 = 0,15 с; а для графика 2 (z= 0,5) – Т 09 – Тзап = Ту1 = 0,08 с, Тн – Ту = = Ту2 = 0,21 с. Таким образом, временные оценки, полученные косвенно из частотных характеристик, качественно совпадают с прямыми оценками, полученными из ПХ. Пример 5.3. Найдем показатели качества и оценим взаимосвязь временных и частотных оценок для ФАПЧ из примера 4.2. Рассмотрим только вариант с наибольшим запасом устойчивости (Т2 = 4,7 мс, k 0 = 200 (46 дБ)). Графики ЛАЧХ и ЛФЧХ разомкнутой системы были построены на рис. 4.12 (график 1). Запас устойчивости по усилению составил >40 дБ, а запас по фазе – примерно 15°, ωср1 = 45 рад/с, ωкр1 = 400 рад/с. Система астатическая первого порядка. Характеристика P (w) показана на рис. 5.7 (график 3). Построим АЧХ замкнутой системы (рис. 5.13), для этого сделаем замену р ® i w в формуле (4.10) и выделим модуль.
Из графика АЧХ находим частотные оценки: М = 4,8, w0 = 44,2 рад/с, wп = 9,5 рад/с, wср = 62,5 рад/с, w07 = 68,8 рад/с, w05 = 76,8 рад/с, z = 0,11. Из графика ПХ определяем временные параметры: Тр = 0,64 с, h max1 = 1,72, γ = 72%, N = 4, h max2 = 1,35, u = 2, а = 4,7 1/с; Тм1 = 70 мс, Тк = 0,14 с (wк = 44,4 рад/с), Тзап = 25 мс, Тн = 38 мс. Подтвердились выводы о колебательности ПХ. Определим некоторые временные параметры по косвенным оценкам. Зная М, найдем с помощью формулы (5.32) запас по фазе: φ з = 13°. С помощью формулы (5.29) оценим Тр: Тр = 0,3…1,3 с. Оценим с помощью формулы (5.30) Тр и γ: Тр = 1 с, γ = 130%. Оценим с помощью формулы (5.42) временные параметры нарастания ПХ: Ту1 = 0 с, Ту2 = 40 мс. Сравним их с временными параметрами, полученными из анализа ПХ на рис. 5.14: Т 09 – Тзап = Ту1 = 35 – 25 = 10 мс, Тн – Ту = Ту2 = 38 – 4 = 34 мс. Пример 5.4. Найдем показатели качества и оценим взаимосвязь временных и частотных оценок для РАС из примера 4.5. Графики ЛАЧХ и ЛФЧХ были построены на рис. 4.14. Запас устойчивости по усилению составил 40 дБ, а запас по фазе – примерно 60°, ωср = 100 рад/с, ωкр = 1000 рад/с. Система статическая. График P (w) показан на рис. 5.15, его поведение напоминает график 2 на рис. 5.7. Согласно косвенным оценкам ПХ должна быть малоколебательной. Построим АЧХ замкнутой РАС (рис. 5.16), для этого найдем H (р):
а затем H (i w) и выделим модуль. H (0) = h (¥) = Sд /(Sд + 1) = 10/11. Построим ПХ замкнутой системы (рис. 5.17), для этого разделим в полученной формуле H (р) на р и выполним обратное преобразование Лапласа.
Из графика ПХ определяем временны
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 867; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.24.176 (0.014 с.) |

 Приведены примеры расчета характеристик радиоавтоматических систем.
Приведены примеры расчета характеристик радиоавтоматических систем. ISBN - технический университет, 2009
ISBN - технический университет, 2009
 . (4.7)
. (4.7) ,
,  ,
,  ,
,  . (4.8)
. (4.8)
 , где W (р) – передаточная функция разомкнутой системы:
, где W (р) – передаточная функция разомкнутой системы: , (4.9)
, (4.9) – коэффициент передачи разомкнутой системы по постоянному току. Зная W (р) (4.9) найдем ПФ замкнутой системы.
– коэффициент передачи разомкнутой системы по постоянному току. Зная W (р) (4.9) найдем ПФ замкнутой системы. . (4.10)
. (4.10)
 . (4.11)
. (4.11) .
. .
. ,
,  ,
,  . (4.12)
. (4.12) Достаточное условие устойчивости требует анализа D2 :
Достаточное условие устойчивости требует анализа D2 : , (4.13)
, (4.13) . (4.14)
. (4.14) .
.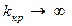 при
при  , то есть в этом случае система будет устойчива при любых k 0.
, то есть в этом случае система будет устойчива при любых k 0.
 . (4.22)
. (4.22) . (4.23)
. (4.23) . (4.24)
. (4.24) . (4.25)
. (4.25) .
.

 , (4.26)
, (4.26) , (5.34)
, (5.34) где z – коэффициент демпфирования.
где z – коэффициент демпфирования. . (5.35)
. (5.35) , (5.36)
, (5.36) . (5.37)
. (5.37) ,
,  . (5.38)
. (5.38) У колебательного звена z < 1.
У колебательного звена z < 1. , то на ПХ (рис. 5.9, график 3) появляется выброс (зона перерегулирования), хотя АЧХ (рис. 5.10) по существу не меняется.
, то на ПХ (рис. 5.9, график 3) появляется выброс (зона перерегулирования), хотя АЧХ (рис. 5.10) по существу не меняется. Хотя при увеличении z уменьшается время запаздывания (Тз1 – Тз4 на рис. 5.9) и увеличивается максимальная скорость нарастания ПХ
Хотя при увеличении z уменьшается время запаздывания (Тз1 – Тз4 на рис. 5.9) и увеличивается максимальная скорость нарастания ПХ  , время регулирования из-за усиления колебательности процесса может даже увеличиться (на рис. 5.9 Тр1 > Тр2 > Тр3 < Тр4).
, время регулирования из-за усиления колебательности процесса может даже увеличиться (на рис. 5.9 Тр1 > Тр2 > Тр3 < Тр4). =
= , (5.39)
, (5.39) . (5.40)
. (5.40) – собственная частота колебаний звена;
– собственная частота колебаний звена;  – коэффициент затухания; также a и wк являются соответственно действительной и мнимой частями корней характеристического уравнения звена (
– коэффициент затухания; также a и wк являются соответственно действительной и мнимой частями корней характеристического уравнения звена ( ) [17, 18]:
) [17, 18]: . (5.41)
. (5.41) Графики звена второго порядка с колебательной ПХ изображены на рис. 5.9 и 5.11.
Графики звена второго порядка с колебательной ПХ изображены на рис. 5.9 и 5.11. ;
;  . (5.42)
. (5.42) , то АЧХ по существу не меняется (рис. 5.10) по сравнению с апериодическим звеном (z ³ 1), хотя на ПХ (рис. 5.9, график 3) появляется выброс.
, то АЧХ по существу не меняется (рис. 5.10) по сравнению с апериодическим звеном (z ³ 1), хотя на ПХ (рис. 5.9, график 3) появляется выброс. Только в случае
Только в случае  наблюдается заметный подъем АЧХ в некотором диапазоне частот, при этом показатель колебательности М и «резонансный горб» увеличиваются с уменьшением z. Обычно резонансная частота w0 несколько ниже wк , но приближается к ней с ростом z.
наблюдается заметный подъем АЧХ в некотором диапазоне частот, при этом показатель колебательности М и «резонансный горб» увеличиваются с уменьшением z. Обычно резонансная частота w0 несколько ниже wк , но приближается к ней с ростом z.
 , (5.43)
, (5.43)



