
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логарифмические частотные характеристики. Диаграммы БодеСодержание книги
Поиск на нашем сайте
В инженерной практике часто пользуются не АЧХ и ФЧХ, а их логарифмическими эквивалентами: логарифмической амплитудно-частотной характеристикой (ЛАЧХ)
и логарифмической фазо-частотной характеристикой (ЛФЧХ)
называемыми также диаграммами Боде.
В последних случаях основные деления сетки частоты отличаются на декаду (в 10 раз). При этом обычно пересечение оси абсцисс с осью ординат выбирают в значении 1 рад/с (1 Гц). В отличие от АЧХ, имеющей линейный масштаб изменения коэффициента передачи вдоль оси ординат, изменение ординаты ЛАЧХ линейно по отношению к приращению функции в дБ. По оси ординат графиков ФЧХ и ЛФЧХ фаза откладывается в градусах либо в радианах. Масштаб линейный. Отличие их в масштабе по оси абсцисс. В первом случае он линейный, во втором – логарифмический. Таким образом, и ЛЧХ, и ЛФЧХ, строго говоря, полулогарифмические характеристики. На рис. 2.4 (графики 1) приведены графики ЛАЧХ и ЛФЧХ для ЧПФ Экспериментально ЛАЧХ и ЛФЧХ исследуются в установившемся режиме. При этом на вход звена или системы подают гармоническое воздействие с постоянной амплитудой x (t) = X0 sin(w t), частота w изменяется либо дискретно, либо непрерывно (например, по линейному закону). В последнем случае период изменения частоты должен быть много больше наибольшей постоянной времени звена (системы). Амплитуда должна быть такой, чтобы во всем диапазоне частот выходная величина оставалась в пределах линейного участка статической характеристики. Если необходимый диапазон частот гармонического воздействия заранее неизвестен, его стараются выбирать не уже интервала, в пределах которого L( w ) превышает уровень–40дБ. Интервал частот выбран правильно, если за его пределами фаза коэффициента передачи изменяется не более чем на 6°. Асимптотические ЛАЧХ и ЛФЧХ. Логарифмические частотные характеристики представляют собой очень удобный и наглядный инструмент анализа и синтеза линеаризованных систем. В инженерной практике принято оперировать не столько реальными логарифмическими характеристиками, сколько их приближенными эквивалентами, так называемыми асимптотическими логарифмическими частотными характеристиками. Для построения асимптотической ЛАЧХ динамического звена первого порядка прежде всего следует выяснить тип звена, определить пределы изменения частоты, коэффициент передачи по постоянному напряжению и частоты сопряжения. Частоты сопряжения легко находятся через постоянные времени звеньев (w j = 1/ Тj). ЧПФ необходимо свести к виду (2.20), для этого числитель и знаменатель нужно представить в виде произведения множителей вида (1 + i w Тj). Если такой множитель будет в знаменателе, его асимптотическая ЛАЧХ до частоты сопряжения w j имеет постоянную асимптоту ЛАЧХ 0 дБ, после w j асимптота линейно убывает со скоростью –20дБ/дек (дБ на декаду или –6 дБ на октаву); а ЛФЧХ до частоты сопряжения w j будет примерно равна 0°, после w j – примерно –90°, на частоте w j = –45°.
Если множитель (1 + i w Тj) окажется в числителе, его асимптотическая ЛАЧХ до частоты сопряжения w j будет постоянной на уровне 0 дБ, после w j асимптота линейно будет возрастать со скоростью +20 дБ/дек; а ЛФЧХ до частоты сопряжения w j будет примерно равна 0°, после w j – примерно +90°, на частоте w j = +45°. Пределы изменения частоты w достаточно ограничить интервалом fmin /30 = 1/30 Тmax... 30 fmax = 30/ Tmin, (2.19) где Тmin и Тmax – соответственно, наибольшее и наименьшее значения постоянных времени звена. На рис. 2.4 (графики 2) построены асимптотические ЛАЧХ и ЛФЧХ. Для их построения необходимо найти частоты сопряжения w 1 = 1/ Т1 = 10 рад/с, w 2 = 1/ Т2 = 100 рад/с. После этого необходимо проанализировать множители.
Звенья в знаменателе: первое (идеальный интегратор) дает асимптоту ЛАЧХ, которая начинается на уровне +40 дБ (k0) при w = 1 и убывает со скоростью –20 дБ/дек; второе (апериодическое) до частоты w1 имеет постоянную асимптоту ЛАЧХ 0 дБ, а после нее асимптота линейно убывает со скоростью –20 дБ/дек. После суммирования асимптотических ЛАЧХ звеньев получим итоговую асимптотическую ЛАЧХ, показанную на рис. 2.4 график 2. На рис. 2.5 показан модуль разности точной и асимптотической ЛАЧХ. Анализ показывает, что точность асимптотических ЛАЧХ вполне достаточна для инженерных расчетов. Максимальная погрешность асимптотической ЛАЧХ получается на частотах сопряжения и не превышает 3 дБ. Для минимально фазовых цепей достаточна грубая оценка ЛФЧХ. Итоговая асимптотическая ЛФЧХ (рис. 2.4 график 2) получается суммированием ЛФЧХ звеньев: интегрирующее звено имеет постоянный фазовый сдвиг –90°, фаза звена первого порядка изменяется с ростом w от 0 до –90° (апериодическое) или от 0 до +90° (форсирующее), проходя на частотах сопряжения через значение ± 45°.
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.196.68 (0.007 с.) |

 (2.17)
(2.17) , (2.18)
, (2.18) По оси абсцисс значения частоты откладываются в логарифмическом масштабе. Причем возможно представление сетки частот в безразмерных единицах lg ω (или lg f) либо в единицах измерения частоты ω – рад/с (или f – Гц).
По оси абсцисс значения частоты откладываются в логарифмическом масштабе. Причем возможно представление сетки частот в безразмерных единицах lg ω (или lg f) либо в единицах измерения частоты ω – рад/с (или f – Гц). при k0 = 100 (40 дБ), Т1 = 0,1 с, Т2 = 0,01 с
при k0 = 100 (40 дБ), Т1 = 0,1 с, Т2 = 0,01 с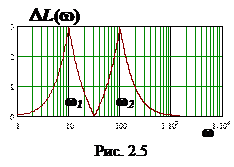 Звено в числителе (форсирующее – классификацию звеньев см. в п. 2.4, а также прил. 2) до частоты w 2 имеет постоянную асимптоту ЛАЧХ 0 дБ, а после нее асимптота линейно возрастает со скоростью +20дБ/дек.
Звено в числителе (форсирующее – классификацию звеньев см. в п. 2.4, а также прил. 2) до частоты w 2 имеет постоянную асимптоту ЛАЧХ 0 дБ, а после нее асимптота линейно возрастает со скоростью +20дБ/дек.


