
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные сведения об устойчивостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте На любую РАС в процессе работы действуют различные возмущения, которые могут нарушить ее нормальную работу. Возникает вопрос об устойчивости системы к любым внешним воздействиям и возмущениям. В простейшем случае понятие устойчивости связано со способностью системы с определенной точностью возвращаться в состояние равновесия (невозмущенное состояние) после исчезновения внешних возмущений, которые вывели РАС из этого состояния. Различают устойчивость состояния равновесия и устойчивость движения. Считается, что строгое определение устойчивости было дано А. М. Ляпуновым в 1892 г. [10]. В упрощенной форме условие устойчивости сформулируем так. Пусть y (t) – траектория возмущенного движения, y0 (t) – траектория невозмущенного движения, а при t = 0 y (t) – y0 (t) = δ(0). В произвольный момент времени ti y (ti) – y0 (ti) = δ(ti). Если при всех t > 0 | y (t) – y0 (t)| ≤ δ(0), а также | y (ti) – y0 (ti)| <δ(ti-1), то динамическая система будет устойчивой. Система асимптотически устойчива, если при t → ∞ δ(t) → 0 область притяжения стягивается в точку): Если система является устойчивой при любых возмущениях, то говорят о глобальной устойчивости. Если вопрос об устойчивости в точке зависит от характера нелинейности и величины возмущений, то речь идёт о локальной устойчивости. Динамика линеаризованной системы описывается уравнением:
где W (p) – ПФ разомкнутой системы. (a0pn + an-1pn-1 +... + an) y (t) = (b0pm + bm-1pm-1 +... + bm) l(t). (4.2) Решение уравнения y (t) = yсв (t) + yвын (t), есть сумма свободной и вынужденной составляющих. Свободная составляющая усв (t) – это решение однородного дифференциального уравнения. anpn + an-1pn-1 +... + a0 = 0. (4.3) Известно, что для полинома n -го порядка существует n корней (в общем случае комплексных) l1, l2,…, ln. Тогда полином (4.3) можно записать в виде an (p – l1)(p – l2)(p – l3)...(p – ln) = 0. (4.4) Для того, чтобы сделать вывод об устойчивости системы, необходимо определить характер переходного процесса. Из дисциплины «Высшая математика» известно, что свободная составляющая yсв (t) описывает переходный процесс системы:
Пусть корень λ j вещественный. Если λ j < 0, то аргумент экспоненты в (4.5) отрицательный, переходный процесс будет иметь затухающий характер (график 1 на рис. 4.1), при λ j > 0 аргумент экспоненты в (4.5) положительный, и переходный процесс будет иметь нарастающий характер (график 2 на рис. 4.1). При λ j = 0 экспонента превратится в константу (график 3 на рис. 4.1). Корни, имеющие мнимые части, образуют комплексно-сопряженные пары: pi = α i + i β i, pi+1 = α i – i β i. Вещественная часть корней соответствует экспоненте в (4.6), мнимая часть – комбинации гармоник (синусов и косинусов) с циклической частотой w = β i: yсв (t) =
На рис. 4.2 представлены графики колебательных переходных процессов для вещественных частей (4.6) различных знаков: график 1 – α j = 0 (постоянные колебания с w = β i), график 2 – затухающий переходный процесс (α j < 0), график 3 – нарастающий переходный процесс (α j > 0). Из проведенного анализа следует, что система будет устойчива, если корни характеристического уравнения лежат в левой комплексной полуплоскости. Если среди корней есть хотя бы один правый корень, то система неустойчива. Если корень имеет нулевую действительную часть, то система будет на границе устойчивости: нейтральной при λ j = 0 (β i = 0 → a0 = 0) или колебательной (β i ¹ 0). Предположим, что все корни левые. Подставим это условие в (4.4). После приведения подобных к виду (4.3) получим важный вывод о положительности коэффициентов aj характеристического полинома. Необходимое условие устойчивости – все коэффициенты характеристического полинома (4.3) должны быть больше нуля. Решение о достаточности условия зависит от значений корней полинома. Пример 4.1. 1. 4 р 5 + 16 р 4 + 8 р 2 + р + 12 = 0 – система неустойчива, так как коэффициент при р 3 равен нулю. 2. 14 р 3 – 7 р 2 + 2 р + 4 = 0 – система неустойчива, так как коэффициент при р 2 отрицательный. 3. р 5 + 7 р 4 + 8 р 3 + 9 р 2 + 4 р + 2 = 0 – необходимое условие устойчивости выполняется, для определения устойчивости РАС необходимо найти корни полинома. (С помощью «Mathcad» можно проверить, что в данном случае все корни лежат в левой комплексной полуплоскости, а значит, система будет устойчивой.)
Для сложных РАС порядок уравнений может быть значительным, и вычисление корней характеристического полинома оказывается затруднительным. Устойчивость можно оценить, не прибегая к вычислениям корней, с использованием алгебраических и графоаналитических критериев, которые были разработаны во времена, когда не было компьютеров. Хотя в настоящее время вычисление корней характеристического полинома даже больших порядков трудностей не представляет, эти критерии не потеряли актуальности. К алгебраическим относятся критерий А. Гурвица, к частотным – критерии А. В. Михайлова, Г. Найквиста и др. Критерий Гурвица В 1877 г. Э. Раусом был предложен алгебраический критерий устойчивости, который в 1895 г. был представлен в более удобной форме А. Гурвицем. Поэтому данный критерий называют также критерием Рауса – Гурвица [10]. Для уравнения (4.3) anpn + an-1pn-1 +...+ a0 =0 составляется матрица Гурвица:
Порядок составления матрицы Гурвица (4.7) такой. По главной диагонали с верхнего левого угла до правого нижнего записываются с убыванием индексов коэффициенты с an-1 по a0. Над элементами главной диагонали записываются коэффициенты с убывающими индексами, а под элементами главной диагонали – с возрастающими. Для оценки устойчивости необходимо вычислить определители Гурвица, которые получаются из (4.7) путем вычеркивания равного числа строк и столбцов в левом верхнем углу матрицы:
Система будет устойчива, если все определители Гурвица при an > 0 – положительные. Если определитель ∆ n = 0, то система находится на границе устойчивости. Возможны два случая: an = 0 или ∆n–1 = 0. Если an = 0, это соответствует нейтрально-устойчивой системе. Если определитель ∆ n-1 = 0, это соответствует колебательной границе устойчивости. Из условия ∆ n-1 = 0 можно определить параметры, при которых РАС находится на границе устойчивости. Это позволяет вычислить критические параметры (например, постоянные времени звеньев, коэффициент усиления по постоянному току kкр), соответствующие границе устойчивости. Отклонение критической величины от номинальной называется запасом устойчивости.
Пример. 4.2. Рассмотрим линеаризованную систему ФАПЧ при отсутствии внешнего возмущения (Sд – крутизна характеристики дискриминатора, Т2 – постоянная времени форсирующего звена). K λ y (p) =
где K λ y (p) = Характеристическое уравнение, которое также можно было получить с помощью формулы (4.1), имеет вид:
Определяем коэффициенты характеристического полинома an: а3 = ТдТф, а2 = Тд + Тф, а1 = 1 + k0Т2, а0 = Составляем матрицу Гурвица:
Находим определители Гурвица:
В данном примере а1, а2, а3 > 0, но а0 зависит от Sд (kи > 0, kф > 0), которая на разных участках дискриминационной характеристики различна (рис. 4.4). Вне рабочего (линейного) участка Sд < 0, и система неустойчива. На рабочем участке Sд > 0, и необходимое условие устойчивости выполняется.
что в итоге позволяет найти критический коэффициент усиления kкр:
Система будет устойчива, если k0 < kкр . Если форсирующее звено в фильтре отсутствует (Т2 = 0), то Если Т2 увеличивается, то kкр также повышается, а значит устойчивость системы увеличивается. Таким образом, в данной РАС, введение форсирующего звена повышает устойчивость системы. Приравняв нулю знаменатель (4.14), получим, что Для анализа устойчивости САУ с характеристическим полиномом выше пятой степени применяют модификацию критерия Гурвица – критерий П. Льенара – Р. Шипара [10], который можно сформулировать так. Если все коэффициенты характеристического полинома положительны (a j > 0), то достаточное условие устойчивости сводится к тому, чтобы положительными были все определители Гурвица либо четного (D2, D4,.., D2k), либо нечетного индекса (D1, D3,.., D2k-1). (Доказано, что из положительности D2 k следует положительность D2 k -1 [10].) В результате количество определителей Гурвица, которые необходимо вычислить, существенно уменьшается.
|
||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1055; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 .
. , (4.1)
, (4.1) yсв (t) =
yсв (t) =  . (4.5)
. (4.5) . (4.6)
. (4.6)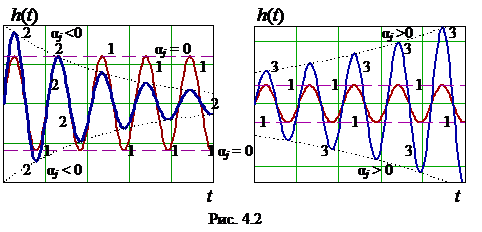
 . (4.7)
. (4.7) ,
,  ,
,  ,
,  . (4.8)
. (4.8)
 , где W (р) – передаточная функция разомкнутой системы:
, где W (р) – передаточная функция разомкнутой системы: , (4.9)
, (4.9) – коэффициент передачи разомкнутой системы по постоянному току. Зная W (р) (4.9) найдем ПФ замкнутой системы.
– коэффициент передачи разомкнутой системы по постоянному току. Зная W (р) (4.9) найдем ПФ замкнутой системы. . (4.10)
. (4.10)
 . (4.11)
. (4.11) .
. .
. ,
,  ,
,  . (4.12)
. (4.12) Достаточное условие устойчивости требует анализа D2 :
Достаточное условие устойчивости требует анализа D2 : , (4.13)
, (4.13) . (4.14)
. (4.14) .
.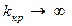 при
при  , то есть в этом случае система будет устойчива при любых k 0.
, то есть в этом случае система будет устойчива при любых k 0.


