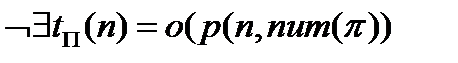Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Кука (NP-полнота задачи «ВЫП»)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Теорема 4 «Теорема Кука» Задачи проверки выполнимости произвольной логической функции в конъюнктивной нормальной форме является Доказательство: Пусть «ВЫП» - идентификатор данной задачи.
Этот факт соответствует набору следующих выражений: G1: В любой момент времени соответсвующая машина Тьюринга находится в одном и только одном состоянии G2: В любой момент времени считывающая головка машины может обозревать одну и только одну ячейку G3: В любой момент времени ячейка в активной зоне может содержать только один символ внутреннего алфавита G4: В начальный момент времени «0» машина находится в конфигурации G5:Не более чем через полиноминальное число шагов машина приходит в состояние G6:В каждый момент времени
Выполнение утверждений G1-G6 означает, что задача принадлежащая классу
Теперь эти утверждение нужно представит в виде КНФ G1:
Получаем порядка Таким образом имея задачу удостоверения мы конструируем КНФ и задача удостоверения сводится к проверке выполнимости КНФ.
Примеры NP-полных задач: 1. Задача «3ВЫП». Пусть 2.
 и числу и числу  узнать, имеется ли в графе узнать, имеется ли в графе  полный подграф с полный подграф с  вершинами (клика). (Граф называется полным, если любые вершины соединены ребром вершинами (клика). (Граф называется полным, если любые вершины соединены ребром 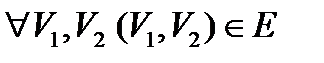 . .
3. Задача «вершинное покрытие» (ВП). Говорят, что некоторое множество вершни 4. Задача «независимые вершины» (НВ). Говорят, что множество вершин 5. Задача «Гамильтонов цикл» (ГЦ). Цикл на графе – это замкнутый путь (замкнутая траектория) состоящая из ребер, при котором каждая из вершин не повторяется дважды. Гамильтонов цикл – это цикл, который проходит все вершины. Гамильтонов цикл – это некое упорядочивование вершин. Для произвольного графа 6. Задача о множестве ребер разрезающих цикл РЦ. Множество ребер разрезающих циклы. Для произвольного графа 7. Задача о множестве вершин разрезающих циклы (ВЦ). Для каждого цикла имеется вершина из этого множества. 8. Задача о изоморфизме подграфу (ИП). Два графа называются изоморфным, если существует отображение одного графа на другой, при котором вершины одного графа переходят в вершины другого графа: 9. Задача целочисленный рюкзак (ЦР). Для произвольных чисел 10. Проблема разрешимости диофантовых уравнений 2-ой степени.
11.
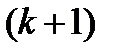 вершину. Соединяем их ребрами следующим образом: если вершину. Соединяем их ребрами следующим образом: если 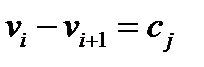 , то соединяем. , то соединяем.
Рассмотрим следующий случай если
Построить граф можем за Число Если пути нет, то Построим пут по шагам: Шаг 0: находимся в вершине 0 Шаг 1: метим все вершины меткой «1», которые можем достичь за один шаг (соединены с вершиной 0 ребром) Шаг 2: для каждой из вершин с меткой «1» находим вершины, которые могут быть достигнуты из вершин с меткой «1» за один шаг и отмечаем их меткой «2» и т. д. Эта процедура требует порядка Если Сложность это алгоритма Нашли ли полиноминальный алгоритм для решения

Значения, которые мы кодируем определяются пропорционально
Такие алгоритмы выделяю в отдельный класс – псевдополиноминальные.
Рассмотрим проблему Под
Задача
Сильная NP-полнота
Теорема 5 «О сильной Если
Доказательство: Пусть
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 577; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.007 с.) |

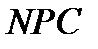
 . Пусть
. Пусть 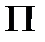 - произвольная задача из
- произвольная задача из 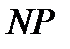 . Необходимо показать, что
. Необходимо показать, что 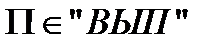 . Для этого множеству индивидуальных задач
. Для этого множеству индивидуальных задач  с ответом «Да» поставим в соответствие недетерминированную машину Тьюринга (НТ), работающая за полиноминальное время. Другими словами существует слово догадка и недетерминированная машина Тьюринга (НТ), которая за определенной число шагов приходит в состояние
с ответом «Да» поставим в соответствие недетерминированную машину Тьюринга (НТ), работающая за полиноминальное время. Другими словами существует слово догадка и недетерминированная машина Тьюринга (НТ), которая за определенной число шагов приходит в состояние 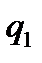 для всех полиноминальных задач имеющих ответ «ДА».
для всех полиноминальных задач имеющих ответ «ДА». 
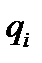
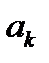 .
.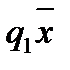
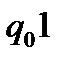
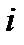 конфигурация машины в следующий момент времени
конфигурация машины в следующий момент времени  определена одной из команд машины НТ.
определена одной из команд машины НТ.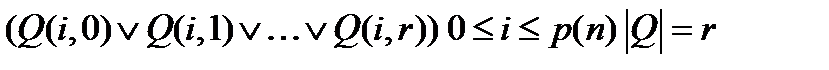 - мощность внутреннего алфавита
- мощность внутреннего алфавита 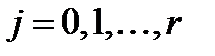
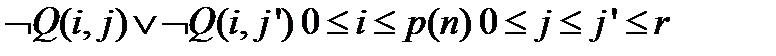 - одновременно в двух состояниях
- одновременно в двух состояниях  находится не может.
находится не может.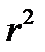 дизъюнкций для каждой из пар
дизъюнкций для каждой из пар  Общее количество переменных будет порядка
Общее количество переменных будет порядка  - полиноминальная оценка задачи, где
- полиноминальная оценка задачи, где 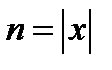 - длина входа.
- длина входа. формула от булевых переменных
формула от булевых переменных  в конъюктивной нормальной форме, где каждая дизъюнкция имеет не более, чем три вхождения переменных. Задача проверки выполнимости таких формул называется задачей 3 – выполнимости («3ВЫП»). Задача «3ВЫП» является NP – полной
в конъюктивной нормальной форме, где каждая дизъюнкция имеет не более, чем три вхождения переменных. Задача проверки выполнимости таких формул называется задачей 3 – выполнимости («3ВЫП»). Задача «3ВЫП» является NP – полной  . Причем
. Причем  формулу с 3-я дизъюнкциями преобразовать в задачу с 2-я дизъюнкциями за полиноминальное число шагов нельзя.
формулу с 3-я дизъюнкциями преобразовать в задачу с 2-я дизъюнкциями за полиноминальное число шагов нельзя.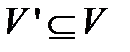 графа
графа 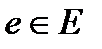 найдется идентичная ему вершина
найдется идентичная ему вершина 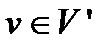 этого множества.
этого множества. 
 графа
графа 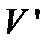 не связаны ребром. Задача о независимом множестве вершин заключается в том, чтобы для произвольного графа
не связаны ребром. Задача о независимом множестве вершин заключается в том, чтобы для произвольного графа  независимое множество из
независимое множество из 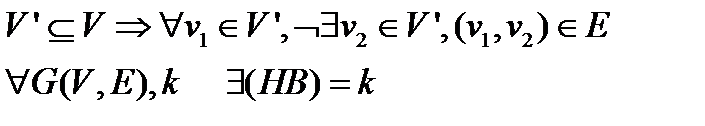
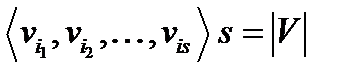 , такая, что выполнено:
, такая, что выполнено: 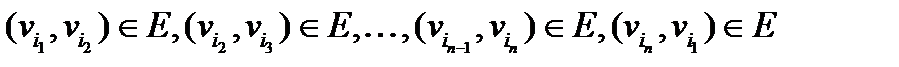 . Задача состоит в том, чтобы выяснить существует ли в графе гамильтонов цикл.
. Задача состоит в том, чтобы выяснить существует ли в графе гамильтонов цикл.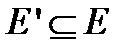 , такое, что
, такое, что 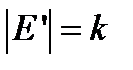 и каждый цикл графа
и каждый цикл графа  .
.
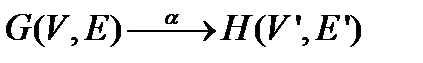
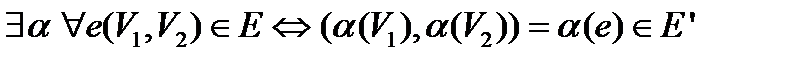
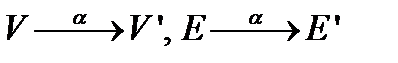 . Задача: для заданных двух графов
. Задача: для заданных двух графов 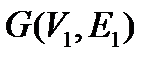 и
и 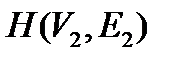 выяснить, содержит ли граф
выяснить, содержит ли граф 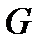 подграф, изоморфный
подграф, изоморфный  .
. и
и  требуется узнать существует ли набор целых чисел
требуется узнать существует ли набор целых чисел 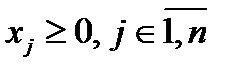 , что выполнено
, что выполнено  . Вариантом задачи является
. Вариантом задачи является  - рюкзак, в которой требуется установить существование
- рюкзак, в которой требуется установить существование 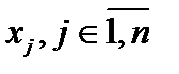 с условием
с условием  Вопрос: разрешимо ли в целых числах?
Вопрос: разрешимо ли в целых числах?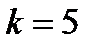 :
: 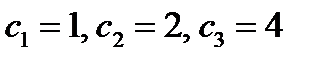
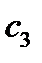
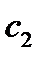

 шагов, где
шагов, где 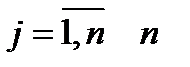 -количество входных чисел
-количество входных чисел 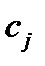 - размерность задачи)
- размерность задачи) , если в графе существует путь по ребрам из нулевой вершины в
, если в графе существует путь по ребрам из нулевой вершины в 
 действий. Если в рамках данной процедуры пометим число
действий. Если в рамках данной процедуры пометим число  -
-  вершин и
вершин и 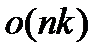 ребер. Если набор ребер упорядочен, то будет
ребер. Если набор ребер упорядочен, то будет  - полной задачи? Другими словами, является ли оценка
- полной задачи? Другими словами, является ли оценка 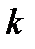

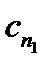




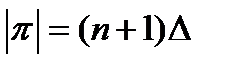 , где
, где  - набор входных параметров (
- набор входных параметров ( и
и 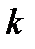 ,
,  - средний размер для кодировки одного параметра.
- средний размер для кодировки одного параметра. 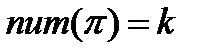
 и зависят от основного машинного алфавита. В
и зависят от основного машинного алфавита. В 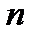 ячейках для двоичной системы кодирования
ячейках для двоичной системы кодирования  . Оценка
. Оценка 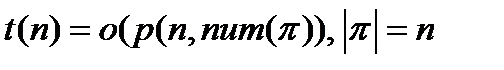

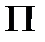 . В ней выделим подпроблему
. В ней выделим подпроблему  , где
, где 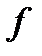 - произвольная функция от параметров задачи:
- произвольная функция от параметров задачи: 

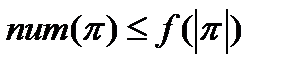
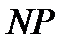 полной, если существует некоторый полином
полной, если существует некоторый полином  для которого подзадача
для которого подзадача 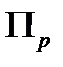 является
является 
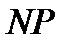 полноте»
полноте»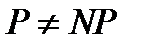 , то никакая сильная
, то никакая сильная 
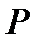 - сильная
- сильная  :
:  . По определению сильной
. По определению сильной 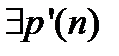 , для которого существует подзадача
, для которого существует подзадача 
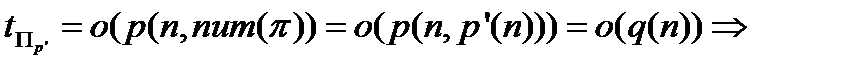 для проблемы
для проблемы  алгоритм разрешения имеет полиноминальную сложность
алгоритм разрешения имеет полиноминальную сложность 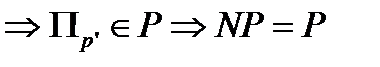 , что противоречит исходному предположению «такого алгоритма не существует» (
, что противоречит исходному предположению «такого алгоритма не существует» (