
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание одноленточной машины ТьюрингаСодержание книги
Поиск на нашем сайте
Техническое устройство, состоящее из: 1. Ленты разделенной на ячейки и бесконечной в обе стороны. В каждой ячейке может быть записан один из символов некоторого множества 2. Управляющее устройство, которое может находиться в одном из внутренних состояний 3. Считывающая головка, которая всякий раз может обозревать только одну ячейку, может перемещаться вдоль лент и может стирать напечатанные символы и печатать новые 4. Команда. Работа машины Тьюринга проходит потактно в зависимости от внутреннего состояния машины и считываемого символа на ленте машина Тьюринга: a) Записывает в эту ячейку символ внешнего алфавита; b) Сдвигает считывающую головку на один шаг влево или один шаг вправо или оставляет её на месте; c) Переходит в новое внутреннее состояние.
Таким образом, работа машины определяется системой команд вида
Где Из набора внутренних состояний выделяют Работа начинается с внутреннего состояния Работа машины заключается в изменении конфигураций. Конфигурация представляет собой совокупность внутреннего состояния, состояния ленты(т.е. размещения букв или слова внешнего алфавита по ячейкам), положения головки на ленте. a
b
Конфигурация Пусть некая конфигурация имеет следующий вид: a Тогда после выполнения команды вида
Стандартная начальная конфигурация имеет вид Тогда работу машины Тьюринга можно представить в следующем виде
…. и набора команд Если приходит в состояние Если машина перешла в состояние
При этом новая машина Тьюринга будет применима только к тем конфигурациям к которым применима исходная машина и результат обеих машин будет одинаковый. Функции, вычислимые по Тьюрингу
Пусть имеется некий алфавит
Рассмотрим функцию отображающую множество слов алфавита на саму себя f: Пусть существует Машина Тьюринга: 1) Если 2) Если Такая машина вычисляет функцию
Чтобы вычислить числовую функцию необходимо договориться о кодировке чисел. Т.е. о способе погружения объектов в заданную сигнатуру. Простейшей кодировкой является унарная кодировка. n ∈ N n = Ι…Ι n+1 = Ι…ΙΙ n = Ι соответствует n=0 Рассмотрим машину Т вычисляющую функцию
Набор команд будет следующим
Для функций нескольких переменных в алфавит вводится символ разделитель «*» Рассмотрим машину Т вычисляющую сумму двух переменных в унарной кодировке.
Пример вида ленты
Набор команд машины Т:
Свойства машин Тьюринга 1. Существование суперпозиции МТ. Пусть есть МТ
Доказательство: Tf1: А1, Q1= Tf2: А2, Q2= Тогда машину Т можно сконструировать следующим образом: Tf: А= А1
Конечное состояние первой машины и начальное состояние второй машины объединим в одно состояние. Переобозначим символы: Q2= Программы машины Tf будут составлены из программ машин Рассмотрим, как будет работать машина Tf:
2. Машина «ИЛИ»:
Принцип работы:
Доказательство: Построим такую МТ:
МТ необходимо дополнить следующими командами:
Прием может быть применен для любых машин Тьюринга
3. Машина «И»
Принцип работы:
Машина, которая после работы оставляет на ленте оба результата через разделитель. Доказательство: А = Тогда машина «И» должна будет проходить через следующие фазы:
Машина Тьюринга «И» - это суперпозиция машин
4. Машина Тьюринга, реализующая цикл:
Тогда существует машина, реализующая цикл
Ф(р)=1
Ф(р)=0 Ф(
Блок-схема алгоритма:
Тезис Тьюринга · Существуют машины, реализующие основные алгоритмические конструкции. Во всех алгоритмах другие конструкции можно представить через эти. · Любой алгоритм всегда может быть реализован с помощью МТ (на данный момент не нашлось алгоритмической процедуры, которая не может быть реализована с помощью МТ). Из этого следует тезис Тьюринга: любая вычислимая функция является вычислимой по Тьюрингу (В=Т) Фактически этот тезис утверждает универсальность машин Тьюринга.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 558; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.90.161 (0.007 с.) |

 называемого внешним алфавитом. При этом один из символов
называемого внешним алфавитом. При этом один из символов  будем считать пустым символом
будем считать пустым символом – внутренний алфавит
– внутренний алфавит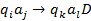
 - внутреннее состояние машины,
- внутреннее состояние машины,  - считываемый символ,
- считываемый символ,  - новое внутреннее состояние,
- новое внутреннее состояние,  - новый записываемый символ,
- новый записываемый символ,  - перемещение головки вдоль ленты: L – влево, R – вправо, E – на месте.
- перемещение головки вдоль ленты: L – влево, R – вправо, E – на месте. где i=1…n, j=0…m имеется только одна команда такого вида. Множество этих команд называется программой машины и в такой программе имеется n(m+1) команд.
где i=1…n, j=0…m имеется только одна команда такого вида. Множество этих команд называется программой машины и в такой программе имеется n(m+1) команд.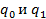 которые объявляются и считаются исходным и заключительным состояниями.
которые объявляются и считаются исходным и заключительным состояниями. , как только машина попадает в состояние
, как только машина попадает в состояние 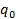 машина Тьюринга останавливается, а слово, которое окажется на ленте является результатом.
машина Тьюринга останавливается, а слово, которое окажется на ленте является результатом.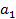

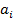




 новая конфигурация будет иметь вид
новая конфигурация будет иметь вид


 в зависимости от слова на ленте
в зависимости от слова на ленте то машина применима к начальной конфигурации. Если же нет, то неприменима.
то машина применима к начальной конфигурации. Если же нет, то неприменима.
 , где
, где  - новое заключительное состояние.
- новое заключительное состояние. – множество слов этого алфавита
– множество слов этого алфавита
 определено и
определено и  , то машина Т применима к начальной конфигурации
, то машина Т применима к начальной конфигурации  и заключитальной конфигурацией является
и заключитальной конфигурацией является 
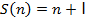

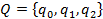












 вычисляющая функцию
вычисляющая функцию  и МТ
и МТ  вычисляющая функцию
вычисляющая функцию  , тогда существует МТ
, тогда существует МТ  вычисляющая суперпозицию
вычисляющая суперпозицию 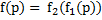
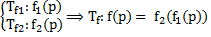


 А2, Q=
А2, Q= 

 .
. p
p 
 f(ε,p) =
f(ε,p) =  , где ε – постоянная, которая может принимать значения 0 или 1.
, где ε – постоянная, которая может принимать значения 0 или 1. ,
, 
 , ε*p
, ε*p при
при 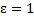
 А= А1
А= А1  , Q=
, Q=  , где
, где  ,
,  .
. 0
0  λR и
λR и  λR
λR *
* 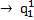 λR
λR 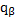 *
*  λR
λR f(p)
f(p) =
=  *
*  , где
, где  ,
, 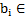 А1
А1  =
=  .
.
 ,
, 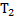 ,
,  и
и  .
.
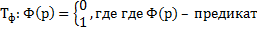
 : Р Ф(
: Р Ф(
 и т.д.
и т.д.





