Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые основные законы распределения непрерывных случайных величинСодержание книги
Поиск на нашем сайте
Равномерное распределение Случайная величина X непрерывного типа называется равномерно распределенной на отрезке [ a, b ] (подчиняется закону R (a, b)), если ее плотность распределения вероятности имеет вид:
При этом для M (X), D (X), s(X) справедливы формулы:
Равномерное распределение реализуется в экспериментах, в которых наудачу ставится точка на отрезке [ a, b ] (X – абсцисса поставленной точки), а также в экспериментах по измерению тех или иных физических величин с округлением (здесь X – ошибка округления). Равномерное распределение имеют ошибки грубых измерений при помощи инструментов с крупными делениями, когда измеренное значение округляется до ближайшего целого (или до ближайшего меньшего, или до ближайшего большего). Например, ошибка (в см) измерения длины с помощью линейки с сантиметровыми делениями имеет равномерное распределение на участке Показательное распределение Непрерывная случайная величина X распределена по показательному закону, если ее плотность распределения имеет вид:
где l – параметр распределения, l > 0. Числовые характеристики СВ Х, имеющей показательное распределение вычисляются по формулам:
Показательное распределение часто встречается в теории массового обслуживания (время ожидания при техническом обслуживании, длительность телефонных разговоров, ежедневно регистрируемых на телефонной станции и др.), а также в теории надежности (срок безотказной работы радиоэлектронной аппаратуры). Если имеется простейший поток событий с интенсивностью l, то величина интервала времени T между двумя соседними событиями имеет показательное распределение с параметром l. Нормальное распределение Непрерывная СВ X имеет нормальное распределение, если ее плотность распределения имеет вид:
где a и s – параметры нормального распределения, s > 0. Функция распределения нормально распределенной СВ X определяется формулой:
Числовые характеристики M (X) и D (X) соответственно равны: Важную роль в теории играет центрированная и нормированная СВ X, для которой a = 0, s = 1. Иногда такое распределение СВ X называется стандартным. Плотность распределения нормальной стандартной СВ
Функция распределения стандартной СВ X имеет вид:
и называется функцией Лапласа. Для удобства вычислений вводят функцию
также называемую функцией Лапласа или нормированной функцией Лапласа. Эти две функции связаны соотношениями:
Функция Лапласа F(X) обладает свойствами: 1) Ф(0) = 0, 2) Ф(– x) = – Ф(x) (нечетная функция); 3) Ф(+¥) = 0,5. График плотности распределения вероятности нормально распределенной СВ X называется нормальной кривой или кривой Гаусса.
Рис. 3 Вероятность попадания значений СВ X, имеющей нормальное распределение с параметрами а и s, на участок (x 1; x 2)выражается формулой:
Если участок (a, b) симметричен относительно a, то вероятность попадания в него
где Нормальное распределение имеет исключительно важное значение в теории вероятностей. Нормальному закону подчиняются, при определенных условиях, ошибки измерений, величины износа деталей в механизмах, ошибки стрельбы, величина шума в радиоприемном устройстве. Главная особенность нормального закона распределения состоит в том, что он является предельным законом, к которому приближаются, при определенных условиях, другие законы распределения. Например, при обработке деталей на станке-автомате, отклонение размеров деталей от номинального вызывается многими причинами. К ним относятся: колебание режима обработки, неточности установки и базировки деталей в приспособлении, износ режущего инструмента, неоднородность обрабатываемого материала, износ деталей станка и т. д. Каждая из этих причин влияет на размер деталей. Поэтому отклонение фактического размера детали от нормального можно представить как сумму большого числа отклонений, вызванных перечисленными выше причинами. Если слагаемые отклонения примерно одного порядка, то суммарное отклонение является случайной величиной, имеющей распределение, асимптотически приближающееся к нормальному. Условия, при которых эти случайные величины Теорема 1. Если случайные величины X 1, X 2, …, Xn независимы, одинаково распределены и имеют конечные M (Xi) = a и D (Xi) = s2 > 0, то
Теорема 2(Ляпунова). Если случайные величины X 1, X 2, …, Xn независимы и имеют конечные M (Xi) = ai,
где
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 224; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.186.26 (0.007 с.) |

 (1.43)
(1.43) (1.44)
(1.44) , если округление производится до ближайшего целого, и на участке [0; 1], если до ближайшего меньшего. Также равномерное распределение имеет ошибка (в мин.) указания времени часами со скачущей минутной стрелкой
, если округление производится до ближайшего целого, и на участке [0; 1], если до ближайшего меньшего. Также равномерное распределение имеет ошибка (в мин.) указания времени часами со скачущей минутной стрелкой  . К случайным величинам, имеющим равномерное распределение, можно отнести также время ожидания пассажиром транспорта, курсирующего с определенным интервалом [0, Т ], угол поворота j хорошо уравновешенного колеса, если оно приводится во вращение и останавливается в результате трения.
. К случайным величинам, имеющим равномерное распределение, можно отнести также время ожидания пассажиром транспорта, курсирующего с определенным интервалом [0, Т ], угол поворота j хорошо уравновешенного колеса, если оно приводится во вращение и останавливается в результате трения. (1.45)
(1.45)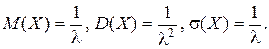 (1.46)
(1.46)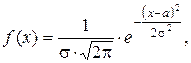 (1.47)
(1.47) (1.48)
(1.48)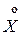 обозначается j(x), где
обозначается j(x), где (1.49)
(1.49) (1.50)
(1.50) (1.51)
(1.51) (1.52)
(1.52)
 (1.53)
(1.53)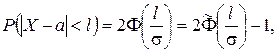 (1.54)
(1.54) – половина длины участка.
– половина длины участка. и
и  асимптотически нормальны, составляют содержание различных формулировок центральной предельной теоремы для одинаково распределенных и различно распределенных случайных величин.
асимптотически нормальны, составляют содержание различных формулировок центральной предельной теоремы для одинаково распределенных и различно распределенных случайных величин.

 тогда
тогда
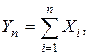



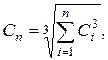 если
если