
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывные и смешанные случайные величиныСодержание книги Поиск на нашем сайте
Многие случайные величины не являются дискретными, например: время безотказной работы прибора, погрешность измерения некоторой величины, расстояние от точки попадания до центра мишени, дальность обнаружения объекта радиолокатором. У всех этих СВ множество возможных значений, совпадает с некоторым промежутком числовой прямой. Если функция распределения F (x) СВ X при любом x непрерывна и, кроме того, имеет производную Если функция распределения F (x) на некоторых участках непрерывно возрастает, а в отдельных точках имеет разрывы I рода, то случайная величина называется смешанной. Функция F (x) для смешанной случайной величины, как и для дискретной, непрерывна слева. Для непрерывной СВ X вероятность принятия этой величиной каждого отдельного значения равна нулю P (X = x) = 0 (1.9) и справедливо утверждение P (a ≤ X < b) = P (a < X < b) = P (a < X ≤ b) = P (a ≤ X ≤ b) = F (b) – F (a). (1.10) Для смешанной случайной величины вероятность принятия этой величиной каждого отдельного значения, принадлежащего участку непрерывности F (x), также равна нулю, а вероятность принятия случайной величиной каждого из тех значений x 1, x 2, …, в которых функция F (x) совершает скачки, численно равна значениям соответствующих скачков. Плотностью распределения вероятности (или плотностью распределения или дифференциальной функцией распределения) непрерывной СВ X называется такая неотрицательная кусочно-непрерывная функция f (x) (PX (x)), что при любых x Î R выполняется равенство
Для любой непрерывной СВ существует плотность распределения. Отметим важные свойства плотности распределения: 1) 2) в точках непрерывности Для непрерывной СВ X с плотностью распределения f (x)
Операции над дискретными случайными величинами Пусть заданы две дискретные случайные величины: СВ X, принимающая значения xi с вероятностями pi = P (X = xi), i = 1, 2, …, n и СВ Y, принимающая значения yj c вероятностями pj = P (Y = yj), j = 1, 2, …, m. Суммой (разностью, произведением) этих случайных величин называется дискретная СВ Z = X + Y (Z = X – Y, Z = X × Y), принимающая значения zij = xi + yj (zij = xi – yj; zij = xi × yj) с вероятностями pij = P (X = xi; Y = yj) для всех указанных значений i и j. В случае совпадения некоторых сумм xi + yj (разностей xi – yj, произведений xi × yj) соответствующие вероятности складываются. Произведением дискретной СВ X на число с называется дискретная случайная величина сX, принимающая значения сxi с вероятностями Аналогично определяются сумма и произведение любого конечного числа дискретных случайных величин. Две дискретные случайные величины X и Y называются независимыми, если события (X = xi) = Ai и (Y = yj) = Bj независимы для любых i = 1, 2, …, n и j = 1, 2, …, m, то есть P (X = xi; Y = yj) = P (X = xi) × P (Y = yj). (1.15) В противном случае СВ X и СВ Y называются зависимыми. Несколько дискретных случайных величин называются взаимно независимыми (независимыми в совокупности), если закон распределения любой из них не зависит от того, какие возможные значения приняли остальные величины. Числовые характеристики случайных величин Закон распределения полностью определяет случайную величину, однако при решении практических задач полезно знать некоторые числовые параметры, характеризующие существенные черты закона распределения случайной величины, ее числовые характеристики. Важнейшими среди них являются характеристики положения: математическое ожидание М (X), мода М 0(X), медиана МД (X) и др.; характеристики рассеивания: дисперсия D (X), среднее квадратическое отклонение s(X) и др. Математическое ожидание Математическим ожиданием дискретной СВ X называется сумма произведений всех ее возможных значений xi на соответствующие им вероятности pi:
Если множество возможных значений СВ X счетно, то сумма, стоящая в правой части равенства будет представлять собой числовой ряд. Математическое ожидание таких СВ X будет существовать, если ряд Математическим ожиданием непрерывной СВ X с плотностью вероятности f(x) называется число
Интеграл в правой части равенства (1.17) должен абсолютно сходиться (в противном случае для непрерывной СВ X М (X) не определено). Математическое ожидание смешанной случайной величины с функцией распределения F (x) вычисляется по формуле
где сумма распространяется на все точки разрыва функции распределения, а интеграл – на все участки ее непрерывности. Математическое ожидание СВ X любого типа характеризует среднее ожидаемое значение СВ X.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 188; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.253.198 (0.005 с.) |

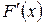 везде, кроме, может быть, отдельных точек разрыва первого рода, то случайная величина называется непрерывной.
везде, кроме, может быть, отдельных точек разрыва первого рода, то случайная величина называется непрерывной. (1.11)
(1.11) (1.12)
(1.12) (1.13)
(1.13) (1.14)
(1.14) (1.16)
(1.16) сходится абсолютно.
сходится абсолютно. . (1.17)
. (1.17) ,
,


