
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение эмпирической функции распределения и гистограммыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Полагая вероятность каждого значения
где При большом объеме Построить интервал, содержащий все выборочные значения, левый и правый концы этого интервала – приближенные (с малым числом значащих цифр) значения наименьшего и наибольшего элементов выборки, причем в первом случае приближение берется с недостатком, а во втором – с избытком. Полученный интервал разделить на m равных частей (интервалов), заботясь при этом (для упрощения вычислений) о том, чтобы границы интервалов были числами с малым количеством значащих цифр. Все расчеты удобно оформить в виде таблицы 2. Выбрав число интервалов m = 20 (оно в процессе обработки может быть изменено), обозначим границы
Таблица 1
Таблица 2
В таких случаях поступают различными способами: а) уславливаются все такие элементы совокупности относить либо к правому, либо к левому интервалу; б) эти элементы учитываются и в левом и в правом интервале, полагая, что в каждый интервал попало по 1/2 элемента. Значения Интервалы, в которые попадает малое число элементов (концевые), рекомендуется объединить. Для построения гистограммы желательно, чтобы число элементов в каждом интервале было не меньше 10, а число интервалов не меньше 8. Уточненные границы интервалов поместим в графу 4, а число элементов, попавших в каждый интервал после уточнения границ, в графу 5. Обозначим середины полученных интервалов через Замечание. При малом объеме выборки в качестве не заполняются. Определим частоту попадания выборочных значений в
где Замечание. При малом объеме выборки частота каждого выборочного значения постоянна и равна 1/n. Эмпирическая функция распределения строится как функция распределения выборки и т. д. (все элементы исходной выборки, попавшие в Очевидно, что для всех
Таким образом, Кроме того,
Значения

1,0 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1
0,18 0,37 0,55 0,74 0,92 1,29 1,85 2,77 Рисунок 1
Если рассматривается выборка из генеральной совокупности значений непрерывной случайной величины, то можно для более наглядного представления о функции распределения генеральной совокупности построить ломаную, соединив точки Замечание. График эмпирической функции распределения можно построить непосредственно, взяв примерно двадцать идущих подряд элементов исходной (до упорядочения) выборки. Гистограмма строится по группированной выборке следующим образом: над каждым интервалом (графа 4) строим прямоугольник, площадь которого равна частоте попадания в данный интервал, т. е. высота прямоугольника равна частоте, деленной на длину соответствующего интервала (рис. 2).
Н
0,18 0,37 0,55 0,74 0,92 1,29 1,85 2,77 х Рисунок 2
Плавная кривая, проведенная по средним точкам верхних оснований прямоугольников гистограммы для выборки из генеральной совокупности значений непрерывной случайной величины, дает представление о графике плотности распределения генеральной совокупности. Замечание. При построении плавной кривой не следует стремиться проводить ее строго через средние точки оснований, так как число элементов, попадающих в каждый интервал, является случайным, и даже в том случае, когда исследуемая случайная величина строго следует закону распределения, характеризуемому плотностью вероятности
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1233; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 равной 1/n, получим распределение выборки. Эмпирическая функция распределения или функция распределения выборки
равной 1/n, получим распределение выборки. Эмпирическая функция распределения или функция распределения выборки  тогда будет определяться следующим образом:
тогда будет определяться следующим образом: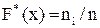 , (1)
, (1) - объем выборки,
- объем выборки,  - число выборочных значений, меньших х.
- число выборочных значений, меньших х. выборку целесообразно предварительно подвергнуть группировке следующим образом.
выборку целесообразно предварительно подвергнуть группировке следующим образом. . Поместим значения границ в графу 2. Подсчитаем число элементов
. Поместим значения границ в графу 2. Подсчитаем число элементов  выборки, попавших в
выборки, попавших в 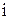 – й интервал. Может случиться, что отдельные значения
– й интервал. Может случиться, что отдельные значения  совпадут со значениями границ некоторых интервалов.
совпадут со значениями границ некоторых интервалов.
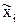





 7
7

 , (2)
, (2) -й интервал,
-й интервал,  , где
, где 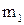 – число уточненных интервалов. Эта сумма должна быть равна единице.
– число уточненных интервалов. Эта сумма должна быть равна единице. , причем значение
, причем значение  повторяется
повторяется  раз,
раз,  раза
раза – й интервал, заменены на
– й интервал, заменены на 
 .
.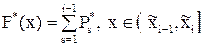 . (3)
. (3) при
при  и
и  при
при 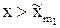 .
. можно поместить в графу 8. Пример графика эмпирической функции распределения представлен на рисунке 1. Доказано, что эмпирическая функция распределения, построенная по всей выборке, сходится по вероятности к функции распределения генеральной совокупности при
можно поместить в графу 8. Пример графика эмпирической функции распределения представлен на рисунке 1. Доказано, что эмпирическая функция распределения, построенная по всей выборке, сходится по вероятности к функции распределения генеральной совокупности при 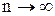 . Но и эмпирическая функция распределения, построенная по группированной выборке, дает достаточно хорошее представление о функции распределения генеральной совокупности.
. Но и эмпирическая функция распределения, построенная по группированной выборке, дает достаточно хорошее представление о функции распределения генеральной совокупности.
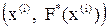 (рис. 1, пунктирная линия).
(рис. 1, пунктирная линия).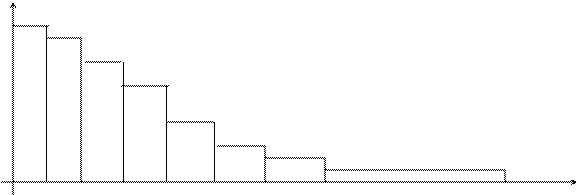
 , эти точки не совпадут точно с точками теоретической кривой.
, эти точки не совпадут точно с точками теоретической кривой.


