Построение доверительного интервала дисперсии
Похожие статьи вашей тематики
В курсе математической статистики доказано, что в выборке из нормальной ге-
неральной совокупности с параметрами  случайная величина случайная величина  , ,
где 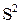 – оценка неизвестной дисперсии, равная – оценка неизвестной дисперсии, равная  , имеет распределение , имеет распределение
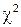 с n степенями свободы. Если параметр с n степенями свободы. Если параметр 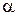 неизвестен, то в выражении неизвестен, то в выражении 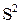 можно заменить можно заменить 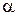 на его оценку на его оценку  ; в этом случае случайная величина ; в этом случае случайная величина  также имеет распределение также имеет распределение 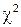 , но уже с , но уже с  , а не с n степенями свободы. , а не с n степенями свободы.
Пусть числа  выбраны таким образом, что выбраны таким образом, что
 , (9) , (9)
где  – заданная доверительная вероятность. – заданная доверительная вероятность.
Равенство (9) означает, что  c вероятностью c вероятностью  . Последнее двойное неравенство эквивалентно следующему: . Последнее двойное неравенство эквивалентно следующему:
 . (10) . (10)
Следовательно,  является доверительным интервалом дисперсии, соответствующим доверительной вероятности является доверительным интервалом дисперсии, соответствующим доверительной вероятности  . .
Однако по заданной вероятности  можно построить множество доверительных интервалов для дисперсии. Принято можно построить множество доверительных интервалов для дисперсии. Принято 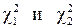 выбирать так, чтобы вероятности выбирать так, чтобы вероятности  были равны и равны были равны и равны  (рис. 1). (рис. 1).
Соответствующие значения 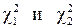 могут быть определены по таблице А2. могут быть определены по таблице А2.
Замечание. При больших объемах выборок можно воспользоваться тем, что рассмотренные оценки математического ожидания и дисперсии распределены
асимптотически нормально.
 
| | | | Рисунок 1. График плотности  - распределения с - распределения с  степенями свободы
степенями свободы 
| |
  x x
Пример выполнения и оформления лабораторной работы
Дана выборка объемом  (табл. 1) из нормальной генеральной совокупности. (табл. 1) из нормальной генеральной совокупности.
Таблица 1
| №
п/п
| Элементы
выборки
| №
п/п
| Элементы
выборки
| №
п/п
| Элементы
выборки
| №
п/п
| Элементы
выборки
| |
| 0,047
|
| 0,496
|
| -1,7888
|
| 0,118
| |
| - 0,451
|
| - 0,748
|
| - 0,855
|
| 0,242
| |
| 1,661
|
| - 0,083
|
| 0,095
|
| 1,739
| |
| 1,290
|
| - 0,312
|
| 1,192
|
| - 0,412
| |
| 0,380
|
| -1,372
|
| - 0,059
|
| - 0,426
|
Найдем по формулам (1) и (3) оценки математического ожидания и дисперсии,  ; ;
 ; ;  . .
Так как объем выборки невелик, для построения доверительного интервала для математического ожидания воспользуемся формулой (8):
 . .
Доверительную вероятность  положим равной 0,95, положим равной 0,95,  . По таблице А3 по заданным . По таблице А3 по заданным  и и  определим определим  . .
Доверительный интервал для математического ожидания, соответствующий доверительной вероятности  : :
 или или  . .
При построении доверительного интервала дисперсии положим  . Тогда . Тогда  . .  определим из условия определим из условия  ; ;  определим из условия определим из условия  (рис. 1). (рис. 1).
По таблице А2 по заданным вероятностям Р (0,01 и 0,99) и заданному числу степеней свободы  находим находим  . .
Доверительный интервал дисперсии, соответствующий доверительной вероятности  , определяется по формуле (10): , определяется по формуле (10):
 . .
Контрольные вопросы
1. Какие оценки параметров называются точечными?
2. Что такое состоятельность, эффективность и несмещенность точечных оценок?
3. В чем состоит метод моментов определения точечных оценок?
4. Что такое доверительный интервал, доверительная вероятность?
5. Что такое 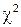 -распределение? -распределение?
6. Чему равны параметры 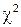 -распределения? -распределения?
7. Охарактеризуйте распределение Стьюдента.
8. Почему рассмотренный способ построения доверительных интервалов применим только при выборке из нормальной генеральной совокупности?
Исходные данные для лабораторной работы 3
| № 1
| № 2
| № 3
| № 4
| № 5
| № 6
| № 7
| № 8
| | 14.0618
| 13.9026
| 9.7201
| 4.5309
| 4.5895
| 1.3838
| 2.7815
| 3.3193
| | 8.3743
| 9.3662
| 7.0484
| 1.6871
| 2.7518
| 2.2614
| 2.0608
| 2.1679
| | 10.5340
| 9.8535
| 10.3314
| 2.7670
| 2.5774
| 2.0527
| 2.6861
| 0.7953
| | 8.3692
| 9.9277
| 9.4375
| 1.6846
| -0.1472
| 4.1610
| 0.3430
| 2.8549
| | 6.1272
| 13.5391
| 2.8829
| 0.5636
| 2.7595
| 5.8933
| 4.1759
| 3. 8020
| | 8.3367
| 9.3665
| 12.8088
| 1.6683
| 4.3083
| 2.0556
| 1.0904
| 2.6005
| | 6.0887
| 5.5420
| 12.9074
| 0.5443
| 3.5989
| 4.2906
| 1.2135
| 1.3975
| | 15.8841
| 11.1165
| 11.0593
| 5.4420
| 3.4770
| 2.7852
| 2.0429
| 1.8426
| | 11.4487
| 12.2644
| 12.3446
| 3.2243
| 2.9288
| 1.0032
| 1.6892
| 1.7857
| | 14.9212
| 5.6033
| 9.6526
| 4.0696
| 1.4865
| 2.9437
| 1.3375
| 4.7483
| | 10.94660
| 8.6225
| 7.5382
| 2.9733
| 3.7393
| 2.2365
| 1.2331
| 3.8656
| | 7.7502
| 18.7922
| 4.8506
| 1.3751
| 1.5352
| 1.8115
| 3.8611
| 2.8041
| | 10.8847
| 5.9896
| 3.8854
| 2.0423
| 1.1407
| 2.9279
| 0.5610
| 1.2308
| | 10.9459
| 6.9886
| 11.0175
| 2.9729
| 4.2322
| 2.6340
| 4.3141
| 1.0685
| | 10.0820
| 12.5703
| 4.2322
| 2.5410
| 2.1104
| 2.0686
| 3.6719
| 1.4731
| | 10.6369
| 11.2834
| 16.3435
| 2.8184
| 2.0427
| 3.6761
| 0.5940
| 0.8569
| | 11.7293
| 11.1766
| 9.7315
| 3.3646
| -1.0828
| 4.9285
| 2.9197
| 1.8717
| | 9.6295
| 8.7034
| 10.0323
| 2.3147
| 0.0672
| 1.6805
| 2.5044
| 3.4308
| | 12.5630
| 11.6438
| 7.9443
| 3.7815
| 2.7772
| 0.0763
| 2.7641
| 1.5044
| | 11.1593
| 9.7334
| 8.0382
| 3.0796
| 1.7421
| 2.3921
| 2.2865
| 1.7567
| | 8.9934
| 13.6365
| 6.5333
| 1.9967
| 2.9660
| 7.2417
| -0.4872
| 3.1034
| | 11.2245
| 7.2417
| 12.0460
| 3.1122
| 4.9154
| 2.8902
| 6.5746
| 0.7403
| | 10.4674
| 2.4929
| 6.5716
| 2.7337
| 4.7761
| -0.3142
| 2.3394
| 1.6882
| | 9.6694
| 9.4939
| 6.5252
| 2.3347
| 0.5675
| 3.3176
| 3.4595
| 5.0764
| | 10.6279
| 16.3353
| 9.8474
| 2.8139
| 2.3807
| 5.8706
| 3.3276
| 1.5786
| | № 9
| № 10
| № 11
| № 12
| № 13
| № 14
| № 15
| № 16
| | 1.7382
| 4.4513
| 2.3600
| 10.2494
| 14.1791
| 7.7676
| 10.5631
| 11.6386
| | -1.3861
| 2.1831
| 1.0242
| 5.6995
| 10.5037
| 9.5229
| 11.1217
| 9.3359
| | -1.6256
| 2.4267
| 2.6657
| 7.4272
| 10.1548
| 9.1054
| 10.3722
| 6.5906
| | 4.6952
| 2.4639
| 2.2187
| 5.6954
| 4.7054
| 13.3220
| 5.6860
| 10.7098
| | 0.4044
| 4.2695
| -1.0585
| 3.9017
| 10.5191
| 16.7866
| 13.3519
| 12.6040
| | 1.7740
| 2.1832
| 3.9044
| 5.6694
| 13.6167
| 9.1112
| 7.1809
| 10.2011
| | 0.3383
| 0.2710
| 3.9537
| 3.8709
| 12.1978
| 11.5813
| 7.4271
| 7.7950
| | 1.5354
| 3.0582
| 3.0296
| 11.7073
| 11.9541
| 10.5705
| 9.0859
| 8.6853
| | 0.2336
| 3.6322
| 3.6723
| 8.1589
| 10.8577
| 7.0065
| 8.3784
| 8.5715
| | 2.1281
| 0.3016
| 2.3263
| 10.9369
| 7.9731
| 10.8874
| 7.6751
| 14.4966
| | 1.8812
| 1.8112
| 1.2691
| 7.7573
| 12.4787
| 9.4730
| 7.4662
| 12.7312
| | 1.5380
| 6.8961
| -0.0746
| 5.2002
| 8.0704
| 8.6231
| 12.7223
| 10.6083
| | 4.7133
| 0.4948
| -0.5572
| 7.7078
| 7.2814
| 10.8569
| 6.1220
| 7.4617
| | 3.4592
| 0.9943
| 3.0087
| 7.7567
| 13.4644
| 10.2680
| 13.6282
| 7.1370
| | 3.8422
| 3.7851
| -0.3638
| 7.0656
| 9.2208
| 9.1373
| 12.3438
| 7.9462
| | 1.1830
| 3.1417
| 5.6717
| 7.5095
| 9.0854
| 12.3522
| 6.1881
| 6.7139
| | 2.2497
| 3.0883
| 2.3657
| 8.3834
| 2.8342
| 14.8570
| 10.8395
| 8.7435
| | 4.5758
| 1.8517
| 2.5161
| 6.7036
| 5.1345
| 8.3611
| 10.0088
| 11.8617
| | 3.8170
| 3.3219
| 1.4721
| 9.0504
| 10.5544
| 5.1526
| 10.5282
| 8.0089
| | 3.1059
| 2.3667
| 1.5191
| 7.9274
| 8.4842
| 9.7842
| 9.5731
| 8.5134
| | -0.2022
| 4.3182
| 0.7666
| 6.1947
| 10.9320
| 19.4835
| 4.0255
| 11.2069
| | 1.4266
| 1.1208
| 3.5230
| 7.9796
| 14.8308
| 10.7805
| 18.1493
| 6.4807
| | 2.6497
| -1.2535
| 0.7858
| 7.3739
| 14.5522
| 4.3714
| 9.6788
| 8.3764
| | 1.2410
| 2.2469
| 0.7626
| 6.7355
| 6.1350
| 11.6352
| 11.9190
| 15.1529
| | 1.9082
| 5.6676
| 2.4237
| 7.5023
| 9.7615
| 16.7412
| 11.6553
| 8.1572
| | № 17
| № 18
| № 19
| № 20
| № 21
| № 22
| № 23
| № 24
| | 8.4764
| 10.3432
| 5.2141
| 7.4505
| 8.3109
| 5.7811
| 10.122
| 6.7761
| | 2.2277
| 7.4030
| 6.6183
| 7.8973
| 6.4687
| 0.7822
| 6.4929
| 4.6387
| | 1.7486
| 7.1239
| 6.2843
| 7.2977
| 4.2724
| 0.3988
| 6.8828
| 7.2651
| | 14.3904
| 2.7643
| 9.6576
| 3.5488
| 7.5678
| 10.5123
| 6.9422
| 6.5500
| | 5.8089
| 7.4153
| 12.4253
| 9.6815
| 9.0832
| 3.6471
| 9.8312
| 1.3063
| | 8.5481
| 9.8934
| 6.2890
| 4.7447
| 7.1609
| 5.8385
| 6.4932
| 9.2470
| | 5.6767
| 8.7583
| 8.2650
| 4.9416
| 5.2360
| 3.5413
| 3.4336
| 9.3259
| | 8.0708
| 8.5633
| 7.4564
| 6.2687
| 5.9482
| 5.4567
| 7.8932
| 7.8474
| | 5.4673
| 7.6861
| 4.6052
| 5.7027
| 5.8572
| 3.3738
| 8.8115
| 8.8757
| | 9.2562
| 5.3784
| 7.7099
| 5.1400
| 10.5973
| 6.4049
| 3.4826
| 6.7221
| | 8.7625
| 8.9829
| 6.5784
| 4.9739
| 9.1850
| 6.0100
| 5.8980
| 5.0306
| | 8.0761
| 5.4563
| 5.8985
| 9.1778
| 7.4866
| 5.4609
| 14.033
| 2.8805
| | 14.4267
| 4.8251
| 7.6847
| 3.8976
| 4.9694
| 10.541
| 3.7917
| 2.1083
| | 11.9385
| 9.7715
| 7.2144
| 9.9026
| 4.7096
| 8.5508
| 5.5909
| 7.8140
| | 12.6844
| 6.3767
| 6.3099
| 8.8750
| 5.3569
| 9.1475
| 9.0562
| 2.3858
| | 7.3661
| 6.2683
| 8.8817
| 3.9504
| 4.3711
| 4.8923
| 8.0267
| 12.0748
| | 9.4994
| 1.2673
| 10.8856
| 7.6716
| 5.9948
| 6.5995
| 7.9413
| 6. 7852
| | 14.1516
| 3.1076
| 5.6889
| 7.0070
| 8.4894
| 10.322
| 5.6527
| 7.0259
| | 12.6341
| 7.4435
| 3.1221
| 7.4225
| 5.4071
| 9.1073
| 8.3151
| 5.3554
| | 11.2119
| 5.7873
| 6.8284
| 6.6585
| 5.8107
| 7.9795
| 6.7867
| 5.4305
| | 4.5955
| 7.7456
| 14.5868
| 2.2204
| 7.9655
| 2.6764
| 9.9092
| 4.2267
| | 7.8532
| 10.8647
| 7.6244
| 13.5195
| 4.1846
| 5.2826
| 4.4933
| 8.6368
| | 10.2995
| 10.6417
| 2.4971
| 6.7430
| 5.7011
| 7.2396
| 0.9943
| 4.2573
| | 7.4821
| 3.9080
| 8.3081
| 8.5352
| 11.1223
| 4.9857
| 6.5951
| 4.2201
| | 8.8164
| 6.8092
| 12.3929
| 8.3243
| 5.5257
| 6.0531
| 12.068
| 6.8779
|
| № 25
| № 26
| № 27
| № 28
| № 29
| № 30
| | 2.7079
| 2.7860
| -1.4882
| 0.3754
| 1.0924
| -1.0156
| | -1.0837
| 0.3358
| -0.3180
| 0.7478
| -0.4427
| -5.1814
| | 0.3560
| 0.1032
| -0.5963
| 0.2481
| -2.2729
| -5.5009
| | -1.0871
| -3.5296
| 2.2147
| -2.8759
| 0.4732
| 2.9269
| | -2.5818
| 0.3461
| 4.5244
| 2.2346
| 1.7360
| -2.7940
| | -1.1088
| 2.4111
| -0.5924
| -1.8793
| 0.1340
| -0.9679
| | -2.6075
| 1.4652
| 1.0542
| -1.7152
| -1.4699
| -2.8821
| | 3.9227
| 1.3027
| 0.3803
| -0.6093
| -0.8764
| -1.2860
| | 0.9658
| 0.5718
| -1.9956
| -1.0810
| -0.9522
| -3.0217
| | 3.2808
| -1.3521
| 0.5916
| -1.5499
| 2.0077
| -0.4958
| | 0.6310
| 1.6524
| -0.3513
| -1.6891
| 1.8208
| -0.8249
| | -1.4998
| -1.2863
| -0.9178
| 1.8148
| 0.4055
| -1.2825
| | 0.5898
| -1.8123
| 0.5706
| -2.5853
| -1.6921
| 2.9511
| | 0.6464
| 2.3096
| 0.1786
| 2.4188
| -1.9086
| 1.2923
| | 0.0546
| -0.5194
| -0.5750
| 1.5625
| -1.3691
| 1.7896
| | 0.4246
| -0.6097
| 1.5681
| -2.5412
| -2.1907
| -1.7559
| | 1.1528
| -4.7771
| 3.2380
| 0.5597
| -0.8376
| -0.3337
| | -0.2469
| -3.2436
| -1.0925
| 0.0059
| 1.2411
| 2.7677
| | 1.7086
| 0.3696
| -3.2315
| 0.3521
| -1.3273
| 1.7561
| | 0.7728
| -1.0105
| -0.1438
| -0.2845
| -0.9910
| 0.8079
| | -0.6710
| 0.6213
| 6.3223
| -3.9829
| 0.8046
| -3.6029
| | 0.8163
| 3.2250
| 0.5200
| 5.4329
| -2.3461
| -1.4311
| | 0.3116
| 3.0348
| -3.7523
| -0.2141
| -1.0823
| 0.1997
| | -0.2203
| -2.5766
| 1.0901
| 1.2793
| 3.4352
| -1.6785
| | 0.4186
| -0.1589
| 4.4941
| 1.1035
| -1.2285
| -0.7890
|
ЛАБОРАТОРНАЯ РАБОТА 4
Линейная регрессия
Порядок выполнения работы
1. Ознакомиться с методическими указаниями.
2. Для данного набора значений независимой переменной 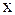 и зависимой переменной и зависимой переменной  , построив точки на плоскости, выдвинуть гипотезу о порядке линейной модели. , построив точки на плоскости, выдвинуть гипотезу о порядке линейной модели.
3. Методом наименьших квадратов найти оценки неизвестных параметров и
построить полученную линию регрессии.
4. Построить доверительные интервалы для оценок неизвестных параметров
для доверительной вероятности  . Проверить гипотезу . Проверить гипотезу  . .
5. Построить доверительные интервалы для предсказанных значений  для доверительной вероятности для доверительной вероятности  и показать их на графике. и показать их на графике.
6. Проверить построенную модель на адекватность.
7. Составить отчет, в котором привести графики, результаты счета, выводы.
8. Ответить устно на контрольные вопросы.
Построение линии регрессии
Связь зависимой переменной с одной или несколькими независимыми пере-
менными представляют в виде уравнения регрессии  . .
Построение уравнения регрессии предполагает решение двух задач:
а) выбор независимых переменных, существенно влияющих на зависимую величину, и определение вида уравнения регрессии;
б) оценивание параметров (коэффициентов) уравнения.
Пусть для одной независимой переменной 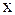 по расположению точек по расположению точек 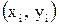 на плоскости выдвинута гипотеза о линейной зависимости между переменными на плоскости выдвинута гипотеза о линейной зависимости между переменными  , т. е. , т. е. 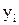 - исход - исход 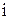 -ого опыта, можно представить в виде: -ого опыта, можно представить в виде:
 , (1) , (1)
где  - число опытов, - число опытов,  - случайные добавки, при учете которых любой индивидуальный - случайные добавки, при учете которых любой индивидуальный 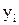 получает возможность не попасть на линию регрессии, получает возможность не попасть на линию регрессии, 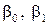 - неизвестные параметры. Предполагается, что - неизвестные параметры. Предполагается, что  распределены нормально с параметрами распределены нормально с параметрами  и независимы. Начнем с предположения, что модель установлена, но на последующих стадиях будем проверять, так ли это на самом деле. Модель (1) линейна относительно неизвестных параметров, относительно неизвестной функции модель (1) первого порядка. и независимы. Начнем с предположения, что модель установлена, но на последующих стадиях будем проверять, так ли это на самом деле. Модель (1) линейна относительно неизвестных параметров, относительно неизвестной функции модель (1) первого порядка.
В соответствии с методом наименьших квадратов оценки параметров 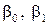 находятся из условия обращения в минимум величины находятся из условия обращения в минимум величины
 (2) (2)
Дифференцируя равенство (2) по 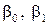 и приравнивая полученные частные производные нулю, для нахождения оценок и приравнивая полученные частные производные нулю, для нахождения оценок  получим так называемую нормальную систему: получим так называемую нормальную систему:
 (3) (3)
Решив систему (3), найдем оценки  неизвестных параметров неизвестных параметров  : :
 (4) (4)
Замечание. Для линейной модели второго порядка
 , ,
нормальная система для нахождения оценок  неизвестных параметров неизвестных параметров  будет иметь вид будет иметь вид
 (5) (5)
Если ввести следующие обозначения

то система (5) может быть записана в виде
 . (6) . (6)
Для модели  , ,  , где , где  - значение - значение  –й независимой переменной –й независимой переменной  , в , в 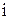 -м опыте, нормальная система также будет иметь вид (6), если -м опыте, нормальная система также будет иметь вид (6), если
 . .
|



 случайная величина
случайная величина  ,
,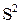 – оценка неизвестной дисперсии, равная
– оценка неизвестной дисперсии, равная  , имеет распределение
, имеет распределение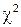 с n степенями свободы. Если параметр
с n степенями свободы. Если параметр 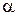 неизвестен, то в выражении
неизвестен, то в выражении  ; в этом случае случайная величина
; в этом случае случайная величина  , а не с n степенями свободы.
, а не с n степенями свободы. выбраны таким образом, что
выбраны таким образом, что , (9)
, (9) – заданная доверительная вероятность.
– заданная доверительная вероятность. c вероятностью
c вероятностью  . (10)
. (10) является доверительным интервалом дисперсии, соответствующим доверительной вероятности
является доверительным интервалом дисперсии, соответствующим доверительной вероятности 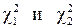 выбирать так, чтобы вероятности
выбирать так, чтобы вероятности  были равны и равны
были равны и равны  (рис. 1).
(рис. 1).

 - распределения с
- распределения с  степенями свободы
степенями свободы 

 x
x (табл. 1) из нормальной генеральной совокупности.
(табл. 1) из нормальной генеральной совокупности. ;
; ;
;  .
. .
. положим равной 0,95,
положим равной 0,95,  и
и  определим
определим  .
. :
: или
или  .
. . Тогда
. Тогда  .
.  определим из условия
определим из условия  ;
;  определим из условия
определим из условия  (рис. 1).
(рис. 1). находим
находим  .
. .
.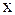 и зависимой переменной
и зависимой переменной  , построив точки на плоскости, выдвинуть гипотезу о порядке линейной модели.
, построив точки на плоскости, выдвинуть гипотезу о порядке линейной модели. . Проверить гипотезу
. Проверить гипотезу  .
. для доверительной вероятности
для доверительной вероятности  .
.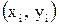 на плоскости выдвинута гипотеза о линейной зависимости между переменными
на плоскости выдвинута гипотеза о линейной зависимости между переменными  , т. е.
, т. е. 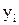 - исход
- исход 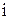 -ого опыта, можно представить в виде:
-ого опыта, можно представить в виде: , (1)
, (1) - случайные добавки, при учете которых любой индивидуальный
- случайные добавки, при учете которых любой индивидуальный 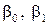 - неизвестные параметры. Предполагается, что
- неизвестные параметры. Предполагается, что  и независимы. Начнем с предположения, что модель установлена, но на последующих стадиях будем проверять, так ли это на самом деле. Модель (1) линейна относительно неизвестных параметров, относительно неизвестной функции модель (1) первого порядка.
и независимы. Начнем с предположения, что модель установлена, но на последующих стадиях будем проверять, так ли это на самом деле. Модель (1) линейна относительно неизвестных параметров, относительно неизвестной функции модель (1) первого порядка. (2)
(2) получим так называемую нормальную систему:
получим так называемую нормальную систему: (3)
(3) неизвестных параметров
неизвестных параметров  :
: (4)
(4) ,
, неизвестных параметров
неизвестных параметров  будет иметь вид
будет иметь вид (5)
(5)
 . (6)
. (6) ,
,  , где
, где  - значение
- значение  –й независимой переменной
–й независимой переменной  , в
, в  .
.


