
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интервальный и дискретный вариационный ряд. Графическое представление статистических рядов.Содержание книги
Поиск на нашем сайте Пусть имеется выборка значений некоторого признака X объёмом n = 50: 9,19 11,5 10,7 12,6 13,0 12,3 7,46 8,92 8,80 11,6 11,9 10,9 5,82 8,89 9,19 11,5 10,7 12,6 13,0 12,3 7,46 8,92 8,80 11,6 11,9 10,9 5,82 8,89 9,32 8,30 8,76 8,01 15,5 12,3 9,46 9,11 12,1 12,5 9,33 11,0 10,1 9,61 13,7 15,0 12,2 13,1 11,7 10,4 11,5 9,02 9,23 7,16 12,0 10,6 6,39 6,97 9,03 6,84 8,29 10,5 11,7 7,05 12,1 9,53 Требуется, разбивая её на k = 6 групп, составить: 1. интервальный вариационный ряд и построить гистограмму частот; 2. дискретный вариационный ряд и построить полигон частот. Поступаем следующим образом. 1. Вводим данные в диапазон А1:А50, выделяем его и щелчком ЛКМ по кнопке 2. из полученного ряда находим значения minX = a1 = 5,82; maxX = a50 = 15,5. Их можно получить также встроенными функциями МИН и МАКС соответственно, диалоговое окно МИН показано на рис. 1:
Рис. 1 3. По формуле =a50-a1 находим размах выборки ΔX = 9,68 4. Оценивая шаг 5. По формуле Оцениваем крайнее левое значение первого интервала, что даёт 5,56. округляем до 5,6 и убеждаемся, что так округлить можно: 5,6+6*1,7 = 15,8>15,5. 6. В диапазоне B1:B7 задаём арифметическую прогрессию, с первым членом 5,6 разностью (шагом) 1,7 предельным значением 15,8:
Рис. 2
7. С помощью встроенной функции СЧЕТЕСЛИ подсчитываем число вариантов, принадлежащих промежутку (5,6 7,3) и записываем результат в ячейку C1:
Рис. 3
Двойные кавычки в поле «Критерий» обязательны. 8. Аналогично подсчитываем и записываем в ячейку C2 число вариантов принадлежащих промежутку (5,6, 9]:
Рис. 4
Продолжая вычисления, приходим к последовательности (рис 5.)
Рис. 5 9. Вводим в ячейку D1 формулу =(B1+B2)/2 и, копированием её, задаём в диапазоне D1:D6 середины интервалов. В ячейку E1 вводим 6, а в ячейку E2 – формулу =C2-C1. Копируя её в ячейки E3:E6, получаем последовательность частот:
Рис. 6 Таким образом, интервальный вариационный ряд выборки записывается в виде
Граничное значение 10,7 отнесено к левому интервалу. Дискретный вариационный ряд задан в диапазоне D1:E6. 10. Графическим редактором «Мастер диаграмм» проводим построение гистограммы частот диапазона E1:E6
Рис. 7
Интервалы указываются на вкладке Ряд (подписи оси X):
Рис.8
11. Полигон частот строим командами Диаграмма ® Нестандартные ® Гистограмма | область:
Рис. 9
В командах Диаграмма ® Нестандартные ® Графики (2 оси) он имеет классический вид:
Рис. 10
Имеются и другие возможности геометрических представлений статистических распределений, включая построение в одной системе координат и полигона, и гистограммы, но на них останавливаться не будем.
Описательная статистика В пакете Анализ данных инструмент Описательная статистика используется для генерации одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных (рис. 11).
Рис. 11 Окно инструмента Описательная статистика Инструмент Описательная статистика использует совокупность методов, позволяющих делать научно обоснованные выводы о числовых параметрах распределения генеральной совокупности по случайной выборке из неё. Пусть требуется изучить количественный признак генеральной совокупности. Если из теоретических соображений ясно, какое именно распределение имеет признак, то с помощью инструмента Описательная статистика можно вычислить следующие параметры: - среднее (статистическую оценку математического ожидания); - стандартную ошибку (среднего)
- медиану; - моду; - стандартное отклонение (среднее квадратическое отклонение); - эксцесс; - асимметрию; - интервал (размах выборки); - минимальное значение выборки; - максимальное значение выборки; - сумму всех значений выборки; - объём выборки;
- наименьшее значение признака, имеющее разность с порядком xmin k единиц; - уровень надёжности (предельная ошибка выборки) Пример. В таблице приведены данные по массе и площади шкуры енотовидной собаки Северо-западного региона и з/х «Пушкинский» (табл.1). Определить средние величины и показатели вариации каждого признака по двум уровням фактора среды обитания.
Табл.1 Масса и площадь шкуры енотовидной собаки Северо-западного региона и з/х «Пушкинский»
Решим данный пример, используя инструмент Описательная статистика. Для этого разместим данные таблицы в ячейках рабочего листа Excel в диапазоне А1:D21 Алгоритм действий следующий: 1. Сервис 2. Входной интервал 3. Группирование 4. Отметить флажком Итоговая статистика; 5. Уровень надёжности: 95 %; 6. К-ый наименьший: 2; 7. К-ый наибольший: 2; 8. ОК. Excel представит результаты, показанные на рис.12
Рис. 12 Таблица результатов решения задачи
Последний параметр «Уровень надежности» позволяет дать интервальную оценку Замечание. Инструментом «Описательная статистика» одновременно могут быть получены числовые характеристики нескольких рядов данных, каждому ряду будет соответствовать свой столбец статистики. Корреляционный анализ В пакете Анализ данных инструмент Корреляция используется для количественной оценки взаимосвязи двух наборов данных, представленных в безразмерном виде. Коэффициент корреляции выборки представляет собой ковариацию двух наборов данных, делённую на произведение их стандартных отклонений (рис. 13)
Рис. 13 Окно инструмента Корреляция
Рассмотрим работу пакета анализа по определению коэффициента корреляции. Пример. Определить степень взаимосвязи между массой и площадью шкуры енотовидной собаки Северо-западного региона (табл.1) Решим пример, используя инструмент Корреляция. Алгоритм действий следующий: 1. Формируем таблицу исходных данных 2. Сервис 3. Входной интервал: А2:В21; 4. Выходной интервал: D3; 5. ОК; Excel представит решение, показанное на рис.14 Вывод: степень взаимосвязи между массой и площадью шкуры енотовидной собаки Северо-западного региона очень слабая, отрицательная.
Рис. 14 Результаты решения задачи с помощью инструмента Корреляция Дисперсионный анализ В пакете Анализ данных инструмент Однофакторный дисперсионный анализ используется для проверки гипотезы о сходстве средних значений двух или более выборок, принадлежащих одной и той же генеральной совокупности (рис. 15) Пример. Установить, влияет ли среда обитания на массу шкуры енотовидной собаки, т.е. проверим гипотезу Но: а1=а2, Решим пример, используя инструмент Однофакторный дисперсионный анализ. Алгоритм действий следующий: 1. Формируем таблицу исходных данных; 2. Сервис 3. Входной интервал: А2:В21; 4. Группирование: по столбцам; 5. Поставить флажок в поле Метки в первом столбце; 6. Альфа: 0,01; 7. Выходной интервал: С1; 8. ОК. Excel представит решение, показанное на рис. 16
Рис. 15 Окно инструмента Однофакторный дисперсионный анализ
Рис. 16 Результаты решения задачи с помощью инструмента Однофакторный дисперсионный анализ Вывод F>Fкрит, следовательно среда обитания влияет на вариацию массы шкуры, т.е. предположение о том, что среда обитания не влияет на вариацию массы шкуры енотовидной собаки не имеет места. Определим долю влияния среды на изучаемый признак
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 869; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |

 располагаем варианты в порядке возрастания.
располагаем варианты в порядке возрастания.
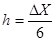 , получаем 1,613333. Округляем (только в большую сторону) и принимаем h = 1,7
, получаем 1,613333. Округляем (только в большую сторону) и принимаем h = 1,7









 ;
;
 - наибольшее значение признака, имеющее разность с порядком хmax k единиц;
- наибольшее значение признака, имеющее разность с порядком хmax k единиц; ,
, Анализ данных
Анализ данных  Описательная статистика
Описательная статистика 
 - найти доверительный интервал, покрывающий
- найти доверительный интервал, покрывающий 

 =0,05. (см.данные табл.1)
=0,05. (см.данные табл.1)

 - доля влияния составляет 94%, оставшиеся 6% вариации обусловлены неучтенными факторами.
- доля влияния составляет 94%, оставшиеся 6% вариации обусловлены неучтенными факторами.


